POJ1673 EXOCENTER OF A TRIANGLE（三角形垂心）

题目链接：

　　http://poj.org/problem?id=1673

题目描述：

EXOCENTER OF A TRIANGLE

 

Description

Given a triangle ABC, the Extriangles of ABC are constructed as follows: 
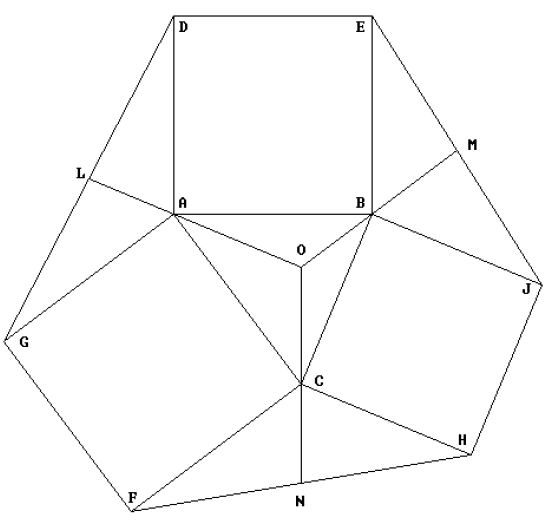
On each side of ABC, construct a square (ABDE, BCHJ and ACFG in the figure below). 
Connect adjacent square corners to form the three Extriangles (AGD, BEJ and CFH in the figure). 
The Exomedians of ABC are the medians of the Extriangles, which pass through vertices of the original triangle,extended into the original triangle (LAO, MBO and NCO in the figure. As the figure indicates, the three Exomedians intersect at a common point called the Exocenter (point O in the figure). 
This problem is to write a program to compute the Exocenters of triangles. 

Input

The first line of the input consists of a positive integer n, which is the number of datasets that follow. Each dataset consists of 3 lines; each line contains two floating point values which represent the (two -dimensional) coordinate of one vertex of a triangle. So, there are total of (n*3) + 1 lines of input. Note: All input triangles wi ll be strongly non-degenerate in that no vertex will be within one unit of the line through the other two vertices.

Output

For each dataset you must print out the coordinates of the Exocenter of the input triangle correct to four decimal places.

Sample Input

2
0.0 0.0
9.0 12.0
14.0 0.0
3.0 4.0
13.0 19.0
2.0 -10.0

Sample Output

9.0000 3.7500
-48.0400 23.3600

 

题目大意：

　　如图，将三边延拓成正方形，然后连线取中点，连线求交点

思路：

　　证明点O为三角形垂心

　　

　　然后可知 CO ⊥ AB

　　另两条边同理

　　求垂心即可

 

　　PS：输出需要加一个EPS，避免-0.000

 

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;

const double EPS = 1e-8;        //精度系数
const double PI = acos(-1.0);    //π

struct Point {
    double x, y;
    Point(double x = 0, double y = 0) :x(x), y(y) {}
    const bool operator < (Point A)const {
        return x == A.x ? y < A.y : x < A.x;
    }
};    //点的定义

typedef Point Vector;    //向量的定义

Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }    //向量加法
Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); }    //向量减法
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }        //向量数乘

Vector Rotate(Vector A, double rad) {
    return Vector(A.x*cos(rad) - A.y*sin(rad), A.x*sin(rad) + A.y*cos(rad));
}    //逆时针旋转rad度

Point LineIntersectionPoint(Point A1, Point B1, Point A2, Point B2) {
    double t1 = ((A1.y - A2.y)*(B2.x - A2.x) - (A1.x - A2.x)*(B2.y - A2.y)) /
        ((B1.x - A1.x)*(B2.y - A2.y) - (B1.y - A1.y)*(B2.x - A2.x));
    return A1 + (B1 - A1)*t1;
}    //返回直线交点

int main() {
    Point A, B, C;
    int n;
    cin >> n;
    while (n--) {
        scanf("%lf%lf%lf%lf%lf%lf", &A.x, &A.y, &B.x, &B.y, &C.x, &C.y);
        Vector v = Rotate(B - A, PI / 2), u = Rotate(C - B, PI / 2);
        Point ans = LineIntersectionPoint(C, C + v, A, A + u);
        printf("%.4lf %.4lf\n", ans.x + EPS, ans.y + EPS);
    }
}