前言:
本文章主要是讲解我个人在学习Java开发环境的排序算法时做的一些准备,以及个人的心得体会,汇集成本篇文章,作为自己对排序算法理解的总结与笔记。
内容主要是关于十大经典排序算法的简介、原理、动静态图解和源码实现的分析。
对于一名程序员来讲,我们都知道数据结构与算法起初是用于C语言居多,然而在Java语言下使用算法的案例却很少,因此,特别整理了在Java开发环境的排序算法,供大家一起学习探讨。
一、排序算法
1.排序算法概述(百度百科):
所谓排序算法,即通过特定的算法因式将一组或多组数据按照既定模式进行重新排序。这种新序列遵循着一定的规则,体现出一定的规律,因此,经处理后的数据便于筛选和计算,大大提高了计算效率。对于排序,我们首先要求其具有一定的稳定性,即当两个相同的元素同时出现于某个序列之中,则经过一定的排序算法之后,两者在排序前后的相对位置不发生变化。换言之,即便是两个完全相同的元素,它们在排序过程中也是各有区别的,不允许混淆不清。
2.《数据结构与算法》中的排序算法
常见的排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。
算法图解(菜鸟教程借图):

图解分析:
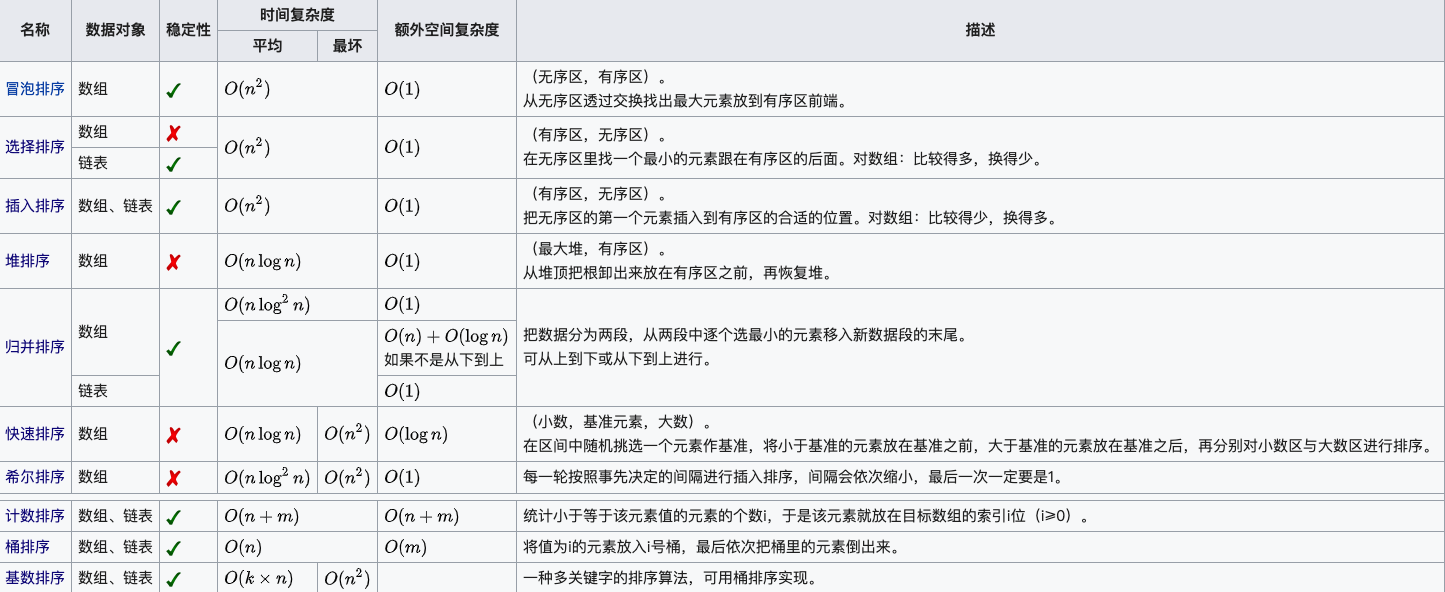
3.算法分析
时间复杂度
平方阶 (O(n2)) 排序 各类简单排序:直接插入、直接选择和冒泡排序。
线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序;
O(n1+§)) 排序,§ 是介于 0 和 1 之间的常数。 希尔排序
线性阶 (O(n)) 排序 基数排序,此外还有桶、箱排序。
关于稳定性
稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序。
不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序。
名词解释:
- n:数据规模
- k:"桶"的个数
- In-place:占用常数内存,不占用额外内存
- Out-place:占用额外内存
- 稳定性:排序后 2 个相等键值的顺序和排序之前它们的顺序相同
- 平均时间复杂度是指所有可能的输入实例均以等概率的出现情况下得到算法的运行时间
- 最坏时间复杂度,一般讨论的时间复杂度均是最坏情况下的时间复杂度,这样做的原因是最坏情况下的时间复杂度是算法在任何输入实例上运行的界限,这就保证了算法的运行时间不会比最坏情况更长。
- 平均时间复杂度和最坏时间复杂度是否一样,这就需要根据算法不同而不同了。
二、十大经典排序算法(Java开发版)
PS:案例均以数组{15,63,97,12,235,66}排序为例
1.冒泡排序
1.1实现原理
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。

1.2动图演示

1.3实例展示
1 import java.util.Arrays;
2 public class BubbleSort {
3 public static void main(String[] args) {
4 int[] arrays =new int[]{15,63,97,12,235,66};
5 for (int i=0;i<arrays.length-1;i++){
6
7 // 控制比较次数,三者交换,实现排序
8 for(int j=0;j<arrays.length-1-i;j++){
9 if (arrays[j] > arrays[j+1]){
10 int temp = 0;//类似空桶
11 temp = arrays[j]; //A桶中水倒入空桶C中
12 arrays[j] = arrays[j+1];//把B桶的水倒入A桶中
13 arrays[j+1] = temp;//把C桶的水倒入B桶中
14 }
15 }
16 }
17 System.out.println(Arrays.toString(arrays));
18 }
19 }排序结果展示:

2.快速排序
快速排序(Quicksort),计算机科学词汇,适用领域Pascal,c++等语言,是对冒泡排序算法的一种改进。
2.1实现原理
快速排序是对冒泡排序的一种改进。通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分所有的数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列

2.2 动图演示

2.3实例展示
1 import java.util.Arrays;
2 public class QuickSort {
3 public static void main(String[] args) {
4 int[] arrays = new int[]{15,63,97,12,235,66};
5 sort(arrays,0,arrays.length-1);
6 System.out.println(Arrays.toString(arrays));
7 }
8 public static void sort(int[] arrays,int left,int right){
9 int l = left;
10 int r = right;
11
12 int pivot = arrays[(left+right)/2];
13 int temp = 0;
14 while (l<r){
15
16 //在左边查找小于中间值的
17 while(arrays[l]<pivot){
18 l++;
19 }
20 //查询右边小于中间值
21 while (arrays[r]>pivot){
22 r--;
23 }
24 if (l>=r){
25 break;
26 }
27 temp = arrays[l];
28 arrays[l] = arrays[r];
29 arrays[r] = temp;
30
31 // 交换完数据arrays[l] = pivot
32 if (arrays[l]==pivot){
33 r--;
34 }
35 if (arrays[r]==pivot){
36 l++;
37 }
38 if (r==l){
39 l++;
40 r--;
41 }
42 if (left<r){
43 sort(arrays,left,r);
44 }
45 if (right>l){
46 sort(arrays,l,right);
47 }
48 }
49 }
50 }排序结果展示:

3.基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
基数排序是1887年赫尔曼、何乐礼发明的。思想是讲整数按位数切割成不同的数字,然后按每个位数分别比较。
3.1实现原理
讲所有的待比较数值统一设置为同样的数位长度,位数比较短的数前面补零,然后从最地位开始依次进行一次排序,这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。

3.2 动图演示

3.3实例展示
1 import java.text.SimpleDateFormat;
2 import java.util.Arrays;
3 import java.util.Date;
4
5 public class BasicSort {
6
7 public static void main(String[] args) {
8 int[] arrays = new int[]{15,63,97,12,235,66};
9 SimpleDateFormat simpleDateFormat =new SimpleDateFormat("yyyy-mm-dd HH:MM:ss:SS");
10 System.out.println("开始排序前:"+simpleDateFormat.format(new Date()));
11 sort(arrays);
12 System.out.println("排序结束:"+simpleDateFormat.format(new Date()));
13 }
14
15 // 1.获取原序列的最大位多少
16 // @param arrays
17 public static void sort(int[] arrays){
18
19 // 获取最大位数
20 int max = 0;
21 for(int i=0;i<arrays.length;i++){
22 if (arrays[i]>max){
23 max = arrays[i];
24 }
25 }
26
27 // 获取字符串长度,所以把int类型转字符串类型
28 int maxLength = (max+"").length();
29
30 // 定义二维数组,大小10,表示10个桶,每一个桶则是一个数组
31 // [[],[],[],[],[]...]
32 int[][] bucket = new int[10][arrays.length];
33
34 // 辅助数组
35 int[] bucketElementCount = new int[10];
36
37 // 循环获取无序数列
38 for (int j=0;j<arrays.length;j++){
39 int locationElement = arrays[j]%10;
40
41 // 放入桶中
42 bucket[locationElement][bucketElementCount[locationElement]] = arrays[j] ;
43 bucketElementCount[locationElement]++;
44 }
45
46 // 遍历每一个桶,讲元素存放原数组中
47 int index = 0;
48 for (int k = 0;k<bucketElementCount.length;k++){
49 if (bucketElementCount[k] !=0){
50 for (int l = 0;l<bucketElementCount[k];l++){
51 arrays[index++] = bucket[k][l];
52 }
53 }
54 bucketElementCount[k] = 0;
55 }
56 System.out.println(Arrays.toString(arrays));
57
58 // 第一轮针对个位数进行比较
59 for (int j = 0;j<arrays.length;j++){
60 int locationElement = arrays[j]/1%10;
61
62 bucket[locationElement][bucketElementCount[locationElement]] = arrays[j];
63 bucketElementCount[locationElement]++;
64 }
65
66 // 取出来按照桶的顺序放回原数组中
67 int indx = 0;
68 for (int k = 0;k<bucketElementCount.length;k++){
69 if (bucketElementCount[k] !=0){
70 for (int l=0;l<bucketElementCount[k];l++){
71 arrays[indx++] = bucket[k][l];
72 }
73 }
74 bucketElementCount[k] = 0;
75 }
76
77 // 判断十位数
78 for (int j = 0;j<arrays.length;j++){
79 int locationElement = arrays[j]/10%10;
80
81 bucket[locationElement][bucketElementCount[locationElement]] = arrays[j];
82 bucketElementCount[locationElement]++;
83 }
84
85 // 取出来按照桶的顺序放回原数组中
86 indx = 0;
87 for (int k = 0;k<bucketElementCount.length;k++){
88 if (bucketElementCount[k] !=0){
89 for (int l=0;l<bucketElementCount[k];l++){
90 arrays[indx++] = bucket[k][l];
91 }
92 }
93 bucketElementCount[k] = 0;
94 }
95




