返回一个数组中的最大子数组和

一、题目：返回一个二维整数数组中的最大子数组的和（随机二维整形数组）

二、课题要求：

输入一个二维整形数组，数组里有正数也有负数；

二维数组中连续的一个子矩阵组成一个子数组，没个子数组都有一个和；

求所有子数组的和的最大值，要求时间复杂度为O(n)。

三、结对编程要求：

两人结对完成编程任务；

一人主要负责程序分析，代码编程；

一人负责代码复审和代码测试计划。

四、设计思路

　　定义一个二维数组，并对其进行随机生成，定义为int32类型，用遍历方法进行计算每个子数组的和，并对其进行比较，结果输出最大子数组的和。

五、程序代码

#include <iostream>
#include <time.h>
using namespace std;
void main()
{
    int x,y,i,j,m=0,A[100][100];
    cout<<"请输入矩阵的行数和列数:";            //输入随机二维整形数组的行数和列数
    cin>>x>>y;
    if(x>100||y>100)
    {
        cout<<"超过行列数范围，请重新输入:";    //保证程序健壮性，超过100行或100列重新输入
        cin>>x>>y;
        cout<<endl;
    }
    int sum[100]={0},max=0,result=A[0][0];


    srand((int)time(0));                        //获得随机二维整形数组
    cout<<"所得随机矩阵如下:"<<endl;
    for(i=0;i<x;i++)
    {
        for(j=0;j<y;j++)
        {
            A[i][j]=-rand()%36+25;
            cout<<A[i][j]<<'\t';
        }
        cout<<endl;
    }


    for(i=0;i<x;i++)                            //进行二维数组中子数组的和计算及比较
    {
        while(m+i<x)
        {

            for(j=0;j<y;j++)
            {
                sum[j]=sum[j]+A[m+i][j];

            }
            max=0;
            for(j=0;j<y;j++)
            {
                if(max+sum[j]>sum[j])
                {
                    max=max+sum[j];
                }
                else
                {
                    max=sum[j];
                }
                if(max>result)
                {
                    result=max;
                }
            }
            m++;
        }

        m=0;
        for(j=0;j<y;j++)
        {
            sum[j]=0;
        }

    }

    cout<<result;                                //获得最大子数组的和
}

六、运行结果

①行列数在100范围以内，直接运行

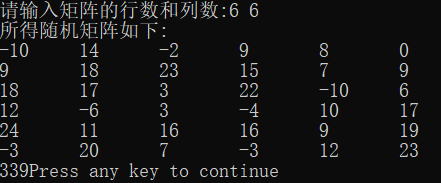
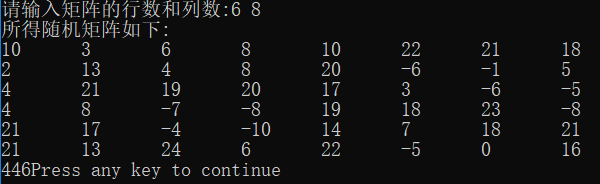
②超过100范围时重新输入

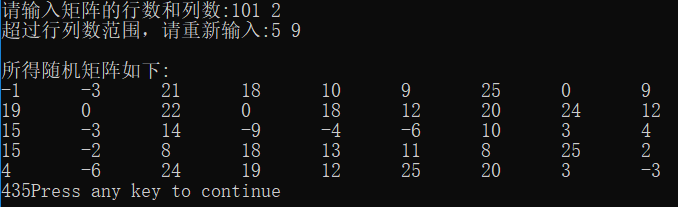
六、收获总结

　　经过这次结对练习，明白了彼此合作的重要性，同时也增加了和队友的相互配合协调能力，对编码也增加了几分熟练。

七、时间记录日志

时间记录日志
日期	开始时间	结束时间	中断时间	净时间	活动
10.20	19:00	21:00	40分钟	80分钟	梳理编程思路，进行三次编写调试
10.21	20:00	22:00	20分钟	100分钟	编写代码调试，编写博客园

八、组员

　　组员博客：姬浩桐：http://www.cnblogs.com/hyjht/

　　组员博客：祁    军：http://www.cnblogs.com/qijun1120/