20190621-N皇后
N皇后
难度分类
困难
题目描述
n皇后问题研究的是如何将 n个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
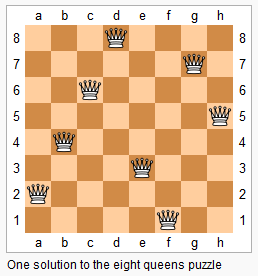
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例:
输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
算法图示
Step1:遍历第一行所有的列,先在第一行的第一个位置放置第一个皇后,第一个皇后放置后其对应的位置以及冲突位置如下:

Step2:遍历第二行所有的列,发现第一第二列冲突,第三列个可以放第二个皇后,放置后如图,放置后对应的位置以及冲突位置如下:
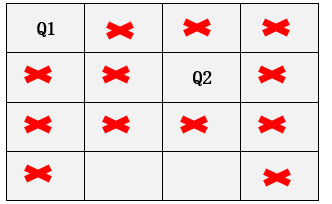
Step3: 遍历第三行所有的列,发现没有位置放置第三个皇后,所有列均冲突,所有此种情况下第三行无法放置第三个皇后(不可能得到最终解)。因此回到第二行,继续遍历第二行的第四列查看是否可以放置第二个皇后,放置后对应位置以及冲突位置如下:

Step4: 在调整了第二个皇后的位置后继续遍历第三行所有的列,发现第二列可以放置第三个皇后,放置后对应位置以及冲突位置如下:Step3: 遍历第三行所有的列,发现没有位置放置第三个皇后,所有列均冲突,所有此种情况下第三行无法放置第三个皇后(不可能得到最终解)。因此回到第二行,继续遍历第二行的第四列查看是否可以放置第二个皇后,放置后对应位置以及冲突位置如下:

Step5: 遍历第四行所有的列,发现没有位置放置第三个皇后,所有列均冲突,此时回到第三步,遍历第三行的第三四列查看是否可以放置第三个皇后,发现均冲突的情况下回到第二行发现第二行的皇后也无法调整位置了回到第一行,将第一行的皇后放在第二列,继续求解放置后对应位置以及冲突位置如下:
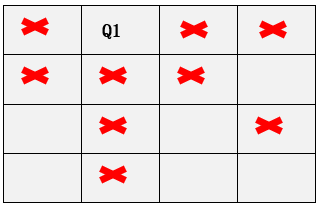
Step6: 在第一行第二列的基础上查看第二行/第三行/第四行依次这样每行的查找,当检查完第一行所有的列后尝试完所有的结果。
算法
根据上面的图示,这种搜索尝试过程中寻找问题的解,但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择。这种解题方法我们可以很容易想到使用回溯算法来解此题,将其转换为算法的步骤如下:
算法第一步
找出约束函数用于去除不合法的解,如图示中已经在第一行第一列的位置放置了皇后的情况下,如果查找放置第二个皇后的约束条件。这里的约束条件如下:
|
01 |
02 |
03 |
04 |
|
11 |
12 |
13 |
14 |
|
21 |
22 |
23 |
24 |
|
31 |
32 |
33 |
34 |
- 判断每次输入的皇后是否在同一行同一列
- 判断每次输入的皇后与以前的皇后是否在同一 ‘/’ 斜线上的位置,此种情况下横纵坐标之和相同
- 判断每次输入的皇后与以前的皇后是否在同一 ‘\’ 斜线上的位置,此种情况下横纵坐标之差相同
转换为伪代码,假定设置2个变量,一个place_queens存放已放置皇后的位置的纵坐标,一个new_queen记录新来的皇后的位置的纵坐标:
- place_queens里面的格式为[x1,x2,x3…],每个x值本身表示其所在的列的索引,每个x本身在place_queens里面的索引表示其所在的行。比如[1,3,0]表示第一行放在第二列,第二行放在第四列,第三行放在第1列,
- 根据a步骤得知len(place_queens)-1表示已放置皇后的最后一行的行号,因此len(place_queens)表示新来的皇后的行号,new_queen的值表示列号
- 如果new_queen与现有place_queens里面的值相等,则证明新皇后与以前的某一个皇后被放到同一列了,因此返回冲突True
- 如果新皇后的行号-新皇后的列号 = 某一已放置皇后的行号-某一已放置皇后的列号即len(placed_queens)-new_queen == pos - placed_queens[pos]则证明新皇后与以前的某一个皇后在同一“\”,因此返回冲突True
- 如果新皇后的行号+新皇后的列号 = 某一已放置皇后的行号+某一已放置皇后的列号即len(placed_queens)+new_queen == pos + placed_queens[pos]则证明新皇后与以前的某一个皇后在同一“/”,因此返回冲突True
- 其他情况不冲突,返回False
算法第二步
实现主函数,根据算法图示我们可以知道八皇后的主要实现就是遍历每一行的每一列,如果能放置皇后,则查看接下来的一行,如果不能放置皇后遍历下一列,这样遍历完所有行的所有列,则可得出N皇后的所有解。得出主体函数就做了2件事:
- 从第一行开始遍历该行的每一列,如果能放置皇后(不冲突),处理下一行,如果不能放置皇后(冲突),继续遍历该行的下一列
- 当处理到最后一行的时候,仍然遍历最后一行的所有列,如果能放置皇后,则找到了一个解,将此解放入结果列表中
算法第三步
我们已经得到了八皇后的解,将其转换为如下格式:
[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
根据前面的算法我们得出N皇后的解的格式如[[1, 3, 0, 2], [2, 0, 3, 1]],映射到题目需要的解,则将[[1, 3, 0, 2], [2, 0, 3, 1]]转换为需要的格式即可具体转换过程为:
- 遍历前声明一个解的列表ans=[]
- 遍历解的每一行,声明每一行的解格式each_row = ['.']*n,
- 然后修改对应位置为Q,修改方式为each_row[row] =’Q’
- 修改后将each_row转换为字符串插入ans中
- 遍历结束后将ans插入result中
- 回溯剪枝
- 列表和字符串转换
考点
回溯
代码
def conflict(placed_queens,new_queen): '''约束函数,用于检查新来的皇后(new_queen)是否和已放置的皇后(placed_queens)是否会互相攻击,如果会返回True,否则返回False''' if new_queen in placed_queens:#如果新的皇后和之前的皇后放置在同一列,纵坐标相等 return True for pos in range(len(placed_queens)):#place_queens里面存储皇后的格式为place_queens[横坐标]=纵坐标 if len(placed_queens)-new_queen == pos - placed_queens[pos]:#在同一 ‘\’ 斜线上的位置,横纵坐标之差相等 return True if len(placed_queens)+new_queen == pos + placed_queens[pos]:#同一 ‘/’ 斜线上的位置,横纵坐标之和相等 return True return False def dfs(n, place_queens=[],result=[]): if len(place_queens) == n - 1:#如果是放置最后一个皇后,即最后一行检查 for i in range(n):#遍历所有的列 if not conflict(place_queens, i):#如果不冲突,放置皇后 place_queens+=[i]# place_queens+=[i]为一个解 #将解转换为目标格式 ans = [] for pos in place_queens: each_row = ['.']*n each_row[pos] ='Q' ans.append(''.join(each_row)) result.append(ans) for i in range(n):#遍历每行所有的列 if not conflict(place_queens, i):#如果不冲突,放置皇后 dfs(n, place_queens + [i],result)#检查下一行可放置皇后位置,place_queens + [i]表示记录当前不冲突的皇后值,放入place_queens中 return result print(dfs(5)
附加代码-N皇后执行步骤辅助理解代码
def confict(place_queens, new_queen): '''place_queens:已放皇后的位置;new_queen:当前要放的皇后的位置''' nextY = len(place_queens) if new_queen in place_queens:#如果要放的位置已经放过了,则肯定冲突 return True '''判断斜线''' for i in range(nextY): #print(len(state), pos, i, state[i]) if nextY-new_queen == i-place_queens[i]: return True#是否在同一 ‘\’ 斜线上,如果要放的位置与现有皇后的位置处于正斜线上则冲突 if nextY+new_queen == i+place_queens[i]: return True#是否在同一 ‘/’ 斜线上,如果要放的位置与现有皇后的位置处于反斜线上则冲突 return False def queens(num, place_queens=(),steps = 1): '''num:皇后的个数,place_queens:已放皇后的位置''' #查看放置皇后位置,Q表示皇后,x表示非皇后 print('当前检查第%s行,已放置皇后的位置:%s'%(steps,place_queens)) if len(place_queens)==num-1:#如果前面已经放了num-1个位置了,当前即为最后一步,此时找到不冲突的位置,返回这个位置 for column in range(num): if not confict(place_queens, column): print('-'*100) print('通知:找到了最后一行的皇后放置位置啦,现告知第%s行!!!'%(steps -1)) print((column,)) yield (column,) else:#如果当前不是最后一步 for column in range(num):#遍历当前行所有的位置 if not confict(place_queens, column):#如果在当前行当前位置上放置皇后不冲突 for result in queens(num, place_queens+(column,),steps+1):#就在当前位置上放置皇后,记录place_queens if steps!=1: print('通知:我们是第%s行,我们已收到通知第%s行的皇后找到了啦,现告知第%s行!!!' % (steps,steps+1,steps-1)) print((column,) + result) else: print('通知:我们已经收到下层反馈,找到了一个解!!!') print((column,) + result) print('-' * 100) yield (column,) + result result = [] num = 4 for each_ans in queens(num): result.append(each_ans) print() print('最终解:',result) print('转换为皇后位置排列如下:') print('-'*100) for each_ans in result: for column in each_ans: temp = ['.'] * num temp[column] = 'Q' print(temp) print('-'*100)





