蓝桥杯2013年省赛c/c++A组题2(排它平方数)
题目标题: 排它平方数
小明正看着 203879 这个数字发呆。 原来,203879 * 203879 = 41566646641,这有什么神奇呢?仔细观察,203879 是个6位数,并且它的每个数位上的数字都是不同的,并且它平方后的所有数位上都不出现组成它自身的数字。具有这样特点的6位数还有一个,请你找出它!
再归纳一下筛选要求:
-
6位正整数
-
每个数位上的数字不同
-
其平方数的每个数位不含原数字的任何组成数位
答案是一个6位的正整数。
请通过浏览器提交答案。
注意:只提交另一6位数,题中已经给出的这个不要提交。
注意:不要书写其它的内容(比如:说明性的文字)。
参考答案: 639172
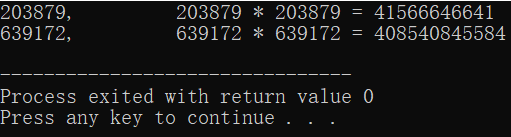
解题C语言代码如下:
/***********************************************************************************************
*** 蓝桥杯2013年省赛c/c++A组题2(排它平方数) ***
***********************************************************************************************
* *
* Project Name : ----------------- *
* *
* File Name : T2排它平方数.c *
* *
* Start Date : 2020-08-05 *
* *
* Last Update : 2020-08-05 [JYH] *
* *
*---------------------------------------------------------------------------------------------*
* Functions: *
* main -- 主函数,寻找排它平方数 *
* isDifferent -- 判断数组中的数字是否各不相同 *
* digital_split -- 数字拆分 *
* number_of_digits -- 计算数字位数 *
* pow1 -- 幂函数 *
* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - */
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int isDifferent(int* data, int n);
void digital_split(long long num, int dig, int* sn);
int number_of_digits(long long num);
long long pow1(int m, int n);
/***********************************************************************************************
* main -- 主函数,寻找排它平方数 *
* *
* INPUT: none *
* *
* OUTPUT: none *
* *
* WARNINGS: none *
* *
* HISTORY: *
* 2020-08-05 JYH : Created. *
*=============================================================================================*/
int main()
{
long long a=99999, aa;
int *data1, *data2;
int dig;
int i,j;
while(a<999999){
a++;
data1 = (int *)malloc(6 * sizeof(int));
digital_split(a, 6, data1);
if(!isDifferent(data1,6)) continue;
aa = a*a;
dig = number_of_digits(aa);
data2 = (int *)malloc(dig * sizeof(int));
digital_split(aa, dig, data2);
for(i=0; i<6; i++){
for(j=0; j<dig; j++){
if(data1[i]==data2[j]){
break;
}
}
if(j!=dig){
break;
}
}
if(i==6){
printf("%lld,\t\t",a);
printf("%lld * %lld = %lld\n",a,a,aa);
}
}
}
/***********************************************************************************************
* isDifferent -- 判断数组中的数字是否各不相同 *
* none *
* *
* INPUT: data -- 需判断的数组 *
* n -- 数组中元素个数 *
* *
* OUTPUT: 1 -- 数组中元素各不相同 *
* 0 -- 数组中至少存在两个元素大小相同 *
* *
* WARNINGS: none *
* *
* HISTORY: *
* 2020-08-05 JYH : Created. *
*=============================================================================================*/
int isDifferent(int* data, int n)
{
int i,j;
for(i=0; i<n; i++){
for(j=i+1; j<n; j++){
if(data[i]==data[j]) return 0;
}
}
return 1;
}
/***********************************************************************************************
* digital_split -- 数字拆分 *
* *
* 对给定数字进行拆分,将每一位存放在数组sn中, sn[0]为个位,sn[1]为十位……以此类推 *
* 注:动态申请一维数组的方法 *
* int *data; *
* data = (int *)malloc(dig * sizeof(int)); *
* 其中:dig为数组位数,int为数组内变量的类型 *
* *
* INPUT: num -- 待拆分数字 *
* dig -- 待拆分数字的位数 *
* sn -- 拆分后每一位存放在数组sn中 *
* *
* OUTPUT: none *
* *
* WARNINGS: 最大可拆18位数字 *
* *
* HISTORY: *
* 2020-08-05 JYH : Created. *
*=============================================================================================*/
void digital_split(long long num, int dig, int* sn)
{
int i;
for(i=0; i<dig; i++){
sn[i] = num/pow1(10,i)%10;
}
}
/***********************************************************************************************
* number_of_digits -- 计算数字位数 *
* *
* 计算数字位数,比如num = number_of_digits(1234) , 输出num=4 *
* *
* INPUT: digits -- 数字 *
* *
* OUTPUT: 数字位数 *
* *
* WARNINGS: 最大可判断18位数字 *
* *
* HISTORY: *
* 2020-08-05 JYH : Created. *
*=============================================================================================*/
int number_of_digits(long long digits)
{
int i;
for(i=17; i>0; i--){
if(digits/pow1(10,i)!=0) break;
}
return i+1;
}
/***********************************************************************************************
* pow1 -- 幂函数 *
* *
* 计算幂函数的值,如:pow(10,5)表示10^5 *
* *
* INPUT: m -- 底数 *
* n -- 指数 *
* *
* OUTPUT: m的n次方(m^n) *
* *
* WARNINGS: none *
* *
* HISTORY: *
* 2020-08-05 JYH : Created. *
*=============================================================================================*/
long long pow1(int m, int n)
{
int i;
long long t=1;
for(i=0; i<n; i++){
t *= m;
}
return t;
}
posted on 2020-08-07 14:54 last_point 阅读(151) 评论(0) 编辑 收藏 举报


