本文首先概述了一些软件复杂度的度量方法,随后介绍了三次作业的构造思路,然后介绍了发现的一些bug以及测试方法,最后进行了总结。
软件复杂度度量方法
圈复杂度v(G):
概念:用来衡量一个模块判定结构的复杂程度。
计算方法:V (G) = P + 1,P为判定节点数,如if,else,case,while等
圈复杂度越大说明程序代码的判断逻辑复杂,可能质量低,且难于测试和维护。
| 圈复杂度 | 代码状况 | 可测试性 | 维护成本 |
|---|---|---|---|
| 1-10 | 清晰 | 高 | 低 |
| 10-20 | 复杂 | 中 | 中 |
| 20-30 | 非常复杂 | 低 | 高 |
| >30 | 不可读 | 不可测 | 非常高 |
基本复杂度ev(G):
概念: 基本复杂度用来衡量程序
计算方法:将模块控制流图中的结构化部分简化成节点,计算简化后控制流图的圈复杂度就是基本复杂度。
模块设计复杂度iv(G):
概念:模块设计复杂度用来衡量模块之间的调用关系,复杂度越高,模块之间耦合性越高,越难隔离,维护和复用。
计算方法:从模块控制流图中移去那些不包含调用子模块的判定和循环结构后得到的圈复杂度。模块设计复杂度通常远小于圈复杂度。
认知复杂度CogC:
这个复杂度比较高级,是为了解决圈复杂度具有的问题而出现的,比如两段代码圈复杂度相同,但是读起来有明显的阅读难度差异。认知复杂度基于三个规则:
-
代码中用到一些语法糖,把多句话缩为一句:代码不会变得更复杂;
-
出现"break"中止了线性的代码阅读理解,如出现循环、条件、try-catch、switch-case、一串的and or操作符、递归,以及jump to label:代码因此更复杂;
-
多层嵌套结构:代码因此更复杂;
第一次作业分析
作业要求概述
读入一个包含加、减、乘、乘方以及括号(其中括号的深度至多为 1 层)的单变量表达式,输出恒等变形展开所有括号后的表达式。因子包括幂函数,常数,以及表达式因子。幂函数以及表达式因子可以有指数。
架构设计思路
很自然的想到将代码分为三个部分:输入解析,拆括号,以及最终合并同类项进行化简,同时需要有一些类作为表达式在程序中的代表,比如代表表达式的Expr类,代表项的Term类。这些代表表达式的结构的类之间应当具有某种引用关系,这种引用关系可以完全反映表达式的结构。
在输入解析部分,采用了递归下降法解析表达式。采用递归下降法而不是正则表达式法是因为正则表达式在处理复杂字符串时很可能由于考虑不周而出错。(事实上这次作业还是因为正则的问题被hack了😇)并且正则无法处理嵌套括号的情况,不利于程序扩展处理多层括号嵌套的表达式。因此,在输入解析部分,程序的流程基本是:读入字符串后首先去除空白字符并合并连续的加减号,然后采用递归下降法解析表达式,最终返回一个Expr引用。有一个处理的trick值得注意:由于合并正负号了,因此我规定只有因子(Expr,Int,Power)才需要考虑正负号的问题,Term不需要考虑这个问题。具体请看下文。
在拆括号部分,我创建了两个处理类ExprExpand与TermExpand,分别处理表达式拆括号与项拆括号。这两个类处理的数据类型包括Expr,Term,以及Factor。表达式拆括号即将表达式带有的指数展开,最终还是一个表达式。项拆括号即将一个项中的含有括号的部分展开,最终成为了一个表达式。事实上拆括号只有这两种类型。这两个类在第一次作业实现后,第二次,第三次都未加修改的使用了。
化简部分是本次作业实现的比较复杂的地方。这是因为化简部分与拆括号部分彻底解耦。化简部分为一个工具类Simplify。拆完括号后调用toString方法将拆完括号的表达式传递给化简部分,化简部分需要重新解析表达式并合并同类项。这里并没有复用递归下降部分的代码,主要原因为如果复用,则最终会返回一个由表达式对象组成的表达式结构,对这个结构进行合并同类项相比于简单的字符串处理更为复杂(还是需要一维的字符串解析)。在第二次作业中,该部分被彻底修改了。
UML类图
从类图可以发现,整个程序分成了四个包,这四个包之间是顺序执行的。这样的划分使得程序结构非常清晰。这说明即使在面向对象的程序中,在某些层面使用面向过程的思想也可以使得程序更加具有可读性。
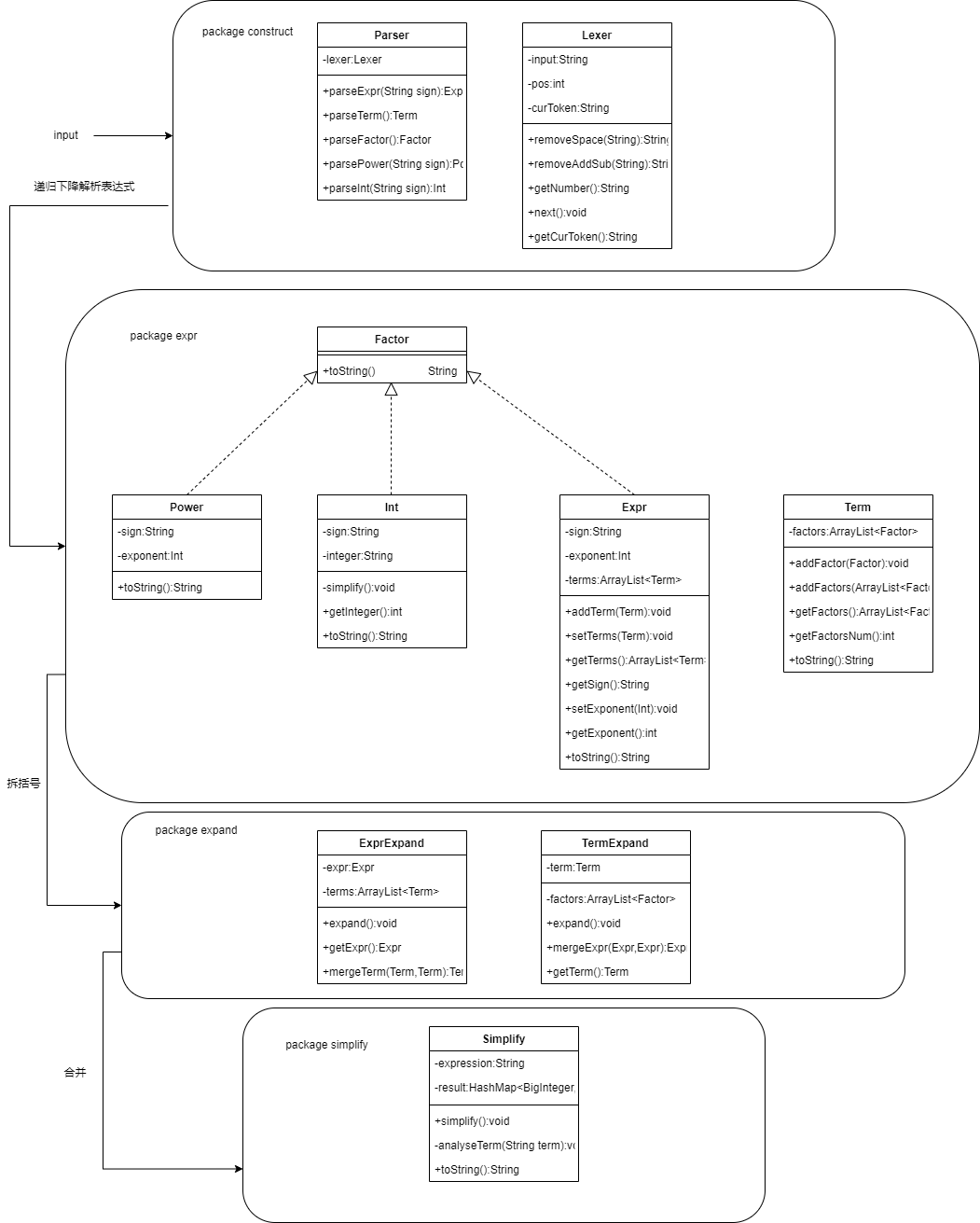
复杂度分析
前两个方法的复杂度较高。可以看到由于simplify的实现问题,其复杂度较高。next方法实际上复杂度并不高,只是由于有很多if条件语句,因此被包含了进来。
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Simplify.simplify() | 21.0 | 1.0 | 10.0 | 11.0 |
| construct.Lexer.next() | 18.0 | 7.0 | 12.0 | 16.0 |
| Simplify.analyseTerm(String) | 12.0 | 1.0 | 8.0 | 8.0 |
| Simplify.toString() | 8.0 | 1.0 | 6.0 | 6.0 |
| expand.TermExpand.expand() | 6.0 | 1.0 | 5.0 | 5.0 |
| construct.Parser.parseExpr(String) | 5.0 | 1.0 | 5.0 | 5.0 |
| construct.Parser.parseFactor() | 5.0 | 1.0 | 5.0 | 5.0 |
| expand.ExprExpand.expand() | 4.0 | 1.0 | 4.0 | 4.0 |
| expand.ExprExpand.mergeTerms(ArrayList, ArrayList) | 3.0 | 1.0 | 3.0 | 3.0 |
| expr.Term.testToString() | 3.0 | 1.0 | 3.0 | 3.0 |
| expr.Term.toString() | 3.0 | 1.0 | 3.0 | 3.0 |
| Simplify.analyseExpr() | 2.0 | 1.0 | 3.0 | 3.0 |
| construct.Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| construct.Parser.parsePower(String) | 2.0 | 1.0 | 2.0 | 2.0 |
| expr.Power.toString() | 2.0 | 3.0 | 1.0 | 3.0 |
| construct.Parser.parseTerm() | 1.0 | 1.0 | 2.0 | 2.0 |
| expand.TermExpand.mergeExpr(Expr, Expr) | 1.0 | 1.0 | 1.0 | 2.0 |
| expr.Expr.setExponent(Int) | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.testToString() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.toString() | 1.0 | 1.0 | 2.0 | 2.0 |
| MainClass.main(String[]) | 0.0 | 1.0 | 1.0 | 1.0 |
| Simplify.Simplify(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Lexer.getCurToken() | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Lexer.removeAddSub(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Lexer.removeSpace(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Parser.Parser(Lexer) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Parser.parseInt(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expand.ExprExpand.ExprExpand(Expr) | 0.0 | 1.0 | 1.0 | 1.0 |
| expand.ExprExpand.getExpr() | 0.0 | 1.0 | 1.0 | 1.0 |
| expand.ExprExpand.mergeTerm(Term, Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| expand.TermExpand.TermExpand(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| expand.TermExpand.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.Expr(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.addTerm(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getSign() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.setTerms(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.Int(String, String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.getInteger() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.simplify() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.testToString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.toString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Power.Power(Int, String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Power.testToString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.Term() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.addFactor(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.addFactors(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getFactors() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getFactorsNum() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.setFactors(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 101.0 | 60.0 | 114.0 | 122.0 |
| Average | 1.9423076923076923 | 1.1538461538461537 | 2.1923076923076925 | 2.3461538461538463 |
第二次作业分析
作业要求概述
读入一系列自定义函数的定义以及一个包含简单幂函数、简单三角函数、简单自定义函数调用以及求和函数的表达式,输出恒等变形展开所有括号后的表达式。
架构设计思路
本次作业中相对于第一次作业加入了自定义函数以及三角函数。虽然自定义函数以及三角函数没有递归调用关系,但是已经出现了潜在的括号嵌套,比如sin的括号外还有一层表达式的括号。因此为了支持这样的表达式解析(以及为了程序的可扩展性而支持嵌套括号或递归调用),表达式解析部分,即construct包内的逻辑是必须要修改的。
但是值得注意的是,到底用不用修改拆括号部分的逻辑呢?如果我们在最终形成的表达式引用关系树中添加新的嵌套的类型,比如自定义函数对象中包含对表达式因子的引用,则拆括号部分是必须要修改的。如果我们仅把改动限定在解析部分,而给后面的逻辑暴露出与第一次作业一样的接口(即表达式树中从拆括号类的视角看不包含新加入的类型。当然可能有新的三角函数类,但是在拆括号类看来这个类就是一个Factor),则拆括号部分的逻辑则不用修改,因为拆括号部分的逻辑已经支持嵌套括号展开了。而这样做的话出bug的几率以及工作量也大幅降低了。因此我选择将改动仅限于表达式解析部分。当然,simplify包中的合并同类项逻辑也是需要重写的。
对表达式解析部分的改动:
新增解析输入自定义函数定义的类Func与FuncSet,以及存放三角函数的Trigo类,Trigo类实现Factor接口。
新增parseSum()与parseFunction()函数,这两个函数均返回一个Expr类型的引用,从程序的其它部分看来行为与parseExpr()相同。
新增parseTrigo()函数,在该函数中会视情况调用其它parse函数处理三角中包含的内容。最后返回一个Trigo类型引用。
新增Sum类与Function类,这两个类当调用parseSum()与parseFunction()时被实例化,并返回给调用函数一个不含自定义函数以及sum的已经展开的字符串。调用函数再实例化Lexer与Parser解析此字符串,并返回一个Expr引用。(这里复用了很多代码,但也导致程序运行时使用了很多内存,使得无法处理长度超过课程组限定长度的字符串。)
对simplify包的重写:
新增Item与Poly类,Item用来存放一个完整的项ax^bsin(...)^ccos(...)^d...,Poly存放所有完整的项。注意到当拆完括号后,返回的表达式树一定形成了这样的结构,否则括号就没有完全展开:
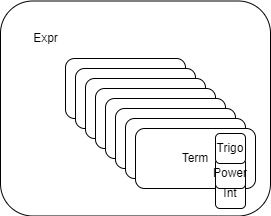
因此在合并同类项时我复用了表达式树的这一结构,在Expr类及Term类中加入了合并同类项相关函数。虽然导致了一些耦合,但是在化简时不用再次解析字符串了。在有三角函数的情况下再次解析字符串的工作量是巨大的。
UML类图
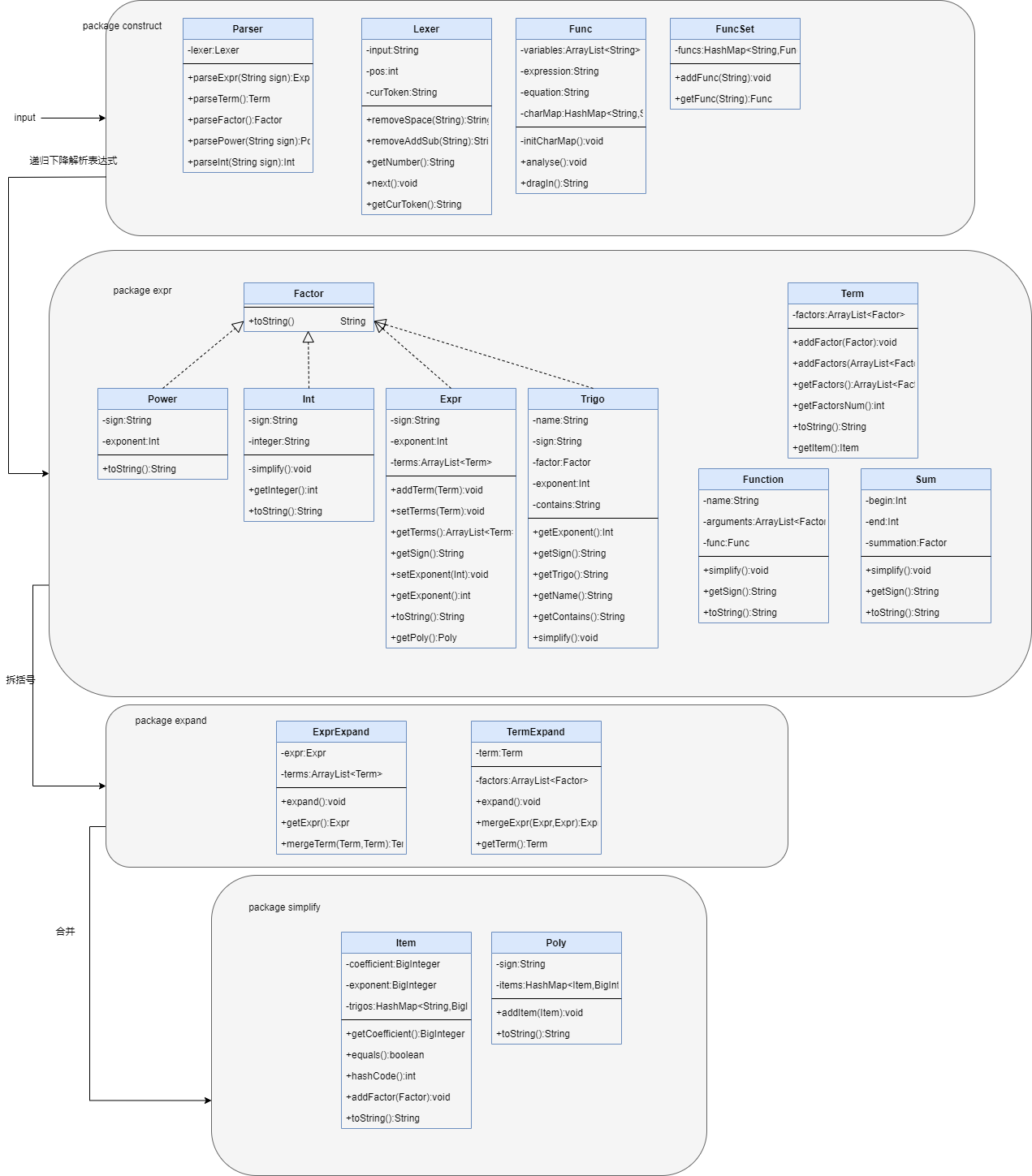
复杂度分析
本次作业的函数数量较上次增加了很多,复杂度较高的方法一共有5个。simplify.Item.addFactor由于需要辨别Factor的具体类型,因此分支较多。simplify.Item.toString()由于需要以最简形式输出,因此有较为复杂的判断逻辑。construct.Parser.parseFactor()是因为加入了自定义函数,求和函数,以及三角函数类的判断,因此增加了分支。然而,除了simplify.Item.toString()较为复杂,其他几个圈复杂度较高的方法实际并不复杂,这从认知复杂度上可以看出来。
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| construct.Lexer.next() | 19.0 | 7.0 | 15.0 | 20.0 |
| simplify.Item.addFactor(Factor) | 17.0 | 6.0 | 10.0 | 12.0 |
| simplify.Item.toString() | 14.0 | 1.0 | 9.0 | 9.0 |
| construct.Parser.parseFactor() | 11.0 | 1.0 | 12.0 | 12.0 |
| expand.ExprExpand.expand() | 11.0 | 1.0 | 7.0 | 7.0 |
| expr.Trigo.toString() | 10.0 | 4.0 | 9.0 | 9.0 |
| simplify.Poly.toString() | 10.0 | 1.0 | 6.0 | 6.0 |
| expr.Power.toString() | 9.0 | 5.0 | 4.0 | 6.0 |
| expr.Trigo.simplify() | 8.0 | 1.0 | 4.0 | 6.0 |
| construct.Parser.parseExpr(String) | 6.0 | 1.0 | 6.0 | 6.0 |
| expand.TermExpand.expand() | 6.0 | 1.0 | 5.0 | 5.0 |
| construct.Parser.parseSum(String) | 4.0 | 1.0 | 5.0 | 5.0 |
| expr.Sum.toString() | 4.0 | 2.0 | 3.0 | 4.0 |
| expr.Term.testToString() | 4.0 | 1.0 | 4.0 | 4.0 |
| expr.Term.toString() | 4.0 | 1.0 | 4.0 | 4.0 |
| expr.Trigo.equals(Object) | 4.0 | 3.0 | 3.0 | 5.0 |
| simplify.Item.equals(Object) | 4.0 | 3.0 | 3.0 | 5.0 |
| construct.Parser.parsePower(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| construct.Parser.parseTrigo(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| expand.ExprExpand.mergeTerms(ArrayList, ArrayList) | 3.0 | 1.0 | 3.0 | 3.0 |
| MainClass.main(String[]) | 2.0 | 1.0 | 2.0 | 3.0 |
| construct.Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| expr.Int.getSign() | 2.0 | 2.0 | 1.0 | 2.0 |
| expr.Term.reverseSign() | 2.0 | 1.0 | 1.0 | 2.0 |
| expr.Trigo.getTrigo() | 2.0 | 2.0 | 1.0 | 2.0 |
| simplify.Poly.addItem(Item) | 2.0 | 1.0 | 2.0 | 2.0 |
| construct.Func.analyse() | 1.0 | 1.0 | 2.0 | 2.0 |
| construct.Func.dragIn(ArrayList) | 1.0 | 1.0 | 2.0 | 2.0 |
| construct.FuncSet.getFunc(String) | 1.0 | 2.0 | 2.0 | 2.0 |
| construct.Lexer.peak(int) | 1.0 | 2.0 | 1.0 | 2.0 |
| construct.Parser.parseFunction(String) | 1.0 | 1.0 | 2.0 | 2.0 |
| construct.Parser.parseTerm() | 1.0 | 1.0 | 2.0 | 2.0 |
| expand.ExprExpand.mergeTerm(Term, Term) | 1.0 | 1.0 | 2.0 | 2.0 |
| expand.TermExpand.mergeExpr(Expr, Expr) | 1.0 | 1.0 | 1.0 | 2.0 |
| expr.Expr.getPoly() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.setExponent(Int) | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.simplify() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.testToString() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Expr.toString() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Function.toString() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Term.getItem() | 1.0 | 1.0 | 2.0 | 2.0 |
| expr.Term.simplify() | 1.0 | 1.0 | 2.0 | 2.0 |
| MainClass.exchangeExponent(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| MainClass.removeSpace(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Func.Func(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Func.initCharMap() | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.FuncSet.FuncSet() | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.FuncSet.addFunc(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Lexer.Lexer(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Lexer.getCurToken() | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Parser.Parser(Lexer, FuncSet) | 0.0 | 1.0 | 1.0 | 1.0 |
| construct.Parser.parseInt(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expand.ExprExpand.ExprExpand(Expr) | 0.0 | 1.0 | 1.0 | 1.0 |
| expand.ExprExpand.getExpr() | 0.0 | 1.0 | 1.0 | 1.0 |
| expand.TermExpand.TermExpand(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| expand.TermExpand.getTerm() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.Expr(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.addTerm(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getSign() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getTerms() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.getTermsNum() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Expr.setTerms(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Function.Function(String, ArrayList, FuncSet) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Function.getSign() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Function.simplify() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Function.testToString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.Int(String, String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.compareTo(Int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.getInteger() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.mult(Int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.simplify() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.testToString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Int.toString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Power.Power(Int, String, String) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Power.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Power.getSign() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Power.simplify() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Power.testToString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sum.Sum(Int, Int, Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sum.getSign() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sum.simplify() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Sum.testToString() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.Term() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.addFactor(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.addFactors(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getFactors() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getFactorsNum() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.getSign() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Term.setFactors(ArrayList) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trigo.Trigo(String, String, Factor, Int) | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trigo.getContains() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trigo.getExponent() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trigo.getName() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trigo.getSign() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trigo.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| expr.Trigo.testToString() | 0.0 | 1.0 | 1.0 | 1.0 |
| simplify.Item.Item(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| simplify.Item.getCoefficient() | 0.0 | 1.0 | 1.0 | 1.0 |
| simplify.Item.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| simplify.Poly.Poly(String) | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 182.0 | 128.0 | 217.0 | 239.0 |
| Average | 1.801980198019802 | 1.2673267326732673 | 2.1485148514851486 | 2.366336633663366 |
第三次作业分析
作业要求概述
读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用以及求和函数的表达式,输出恒等变形展开所有括号后的表达式。
架构设计思路
第三次作业在第二次作业的基础上增加了自定义函数递归嵌套调用,以及三角函数的嵌套调用。但是只要按照形式化定义使用递归下降法解析,就不会有问题。本次作业的架构与实现与第二次作业基本一致。
UML图

bug分析与测试方法
出现bug的方法与未出现bug的方法在代码行和圈复杂度上并没有明显差异。事实上出bug更多是因为对工具的运用不熟练(正则表达式),或者对作业的某些要求没有理解清楚而导致的。
第一次作业bug
强测未发现bug,互测被hack了两次,发现是使用正则将所有1*替换掉了,而这样会导致21*x变为2x。
互测未发现别人的bug。
第二次作业bug
强测互测均未测出bug,发现有的同学sum没有处理下界可能是负数的情况。
第三次作业bug
强测有一个数据点未通过,是因为由于没有考虑到三角函数中有可能包含的表达式因子的所有情况,导致缺少括号。
互测方法
互测采用了大量数据覆盖性测试以及特殊数据针对性测试相结合的方式,全部使用自动化测试工具完成。特殊数据的生成主要是通过查看被测代码中使用正则表达式替换与提取的部分。
测试工具
第一次作业比较简单,使用python完成了一个数据生成器以及自动化测试工具。第二三次作业数据生成比较复杂,仅完成了自动化测试工具,数据生成使用的是翁英杰同学的神仙代码。
心得体会
-
如果要拿分,优化需要认真做:我的第二次第三次作业中仅对基本情况,比如sin(0),cos(0)进行了优化,导致性能分拉胯。
-
需要考虑可扩展性:注重可扩展性,第一次作业的拆括号逻辑可以一直用到第三次作业。
-
正则表达式很好用,字符串处理工具类很好用,IDEA很好用,迭代器很好用,容器很好用。
-
对java内存布局及管理仍然概念模糊:最直接的一个障碍就是深拷贝浅拷贝的问题。虽然在做作业的过程中将引用类比C的指针,小心避开了拷贝的陷阱,但是仍然对java内存管理没有很清晰的概念。之后应当把这里搞明白。
-




