后缀数组
后缀数组略讲
参考文献: IOI2009 国家集训队论文 后缀数组 罗穗骞
什么是后缀数组?
后缀数组是一个十分不好理解并且不好实现的字符串算法,但是它很重要,因为它可以实现后缀树的大部分操作。而且内存比后缀树要小很多。
后缀数组的实现
基本定义
声明:本人的字符串全部从0开始
后缀:后缀指从某一个位置i到整个字符串的末尾结束的一个子串,我们称它为Suf(i)。
长度:字符串的长度,记为n,即n=S.size();
大小比较:按字典序比较
后缀数组SA:它保存 S串的n个后缀从小到大按字典序排序后每一个后缀的开头位置,简单的说,后缀数组是“排第几的是谁? ” 。
排名数组Rank:它保存 S串的每一个后缀在排好序后的位置,简单的说,名次数组是“你排第几? ” 。
举个例子:S="ababa";
Suf(0)="ababa"; Suf(3)="ba"; n=5;
| 按字典序排序后是: |
|---|
| a |
| aba |
| ababa |
| ba |
| baba |
| 下标 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| SA数组 | 5 | 3 | 1 | 4 | 2 |
| Rank数组 | 3 | 5 | 2 | 4 | 1 |
倍增
思路:枚举长度2^k,然后枚举全部的Rank值,以当前Rank值为第一关键字,当前的位置加上长度的Rank值为第二关键字,越界的第二关键字为一个很小的数。
然后先按第一关键字排序,再按第二关键字排序,计算出新的Rank值。直到全部的Rank值都不一样了,那么现在的Rank值即为最终Rank值,退出循环。
所以倍增的理论复杂度是O(nlogn),但实际复杂度却可能跑的很快。
随便说一下,刚开始的Rank值为ASCII码或其他的有序值。
以字符串"aabaaaab"为例,模拟的图:
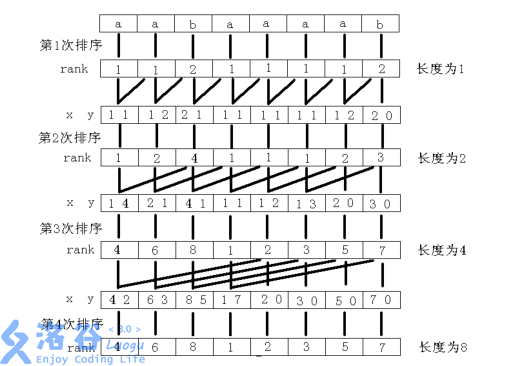
倍增实现————快速排序
前面说了,倍增时间复杂度是O(nlogn)的,其实那样的排序方式要用O(n)的排序,但那样的方法不好理解,所以这里先讲快速排序,总体时间复杂度为O(n logn logn).
//luogu P3809 【模板】后缀排序
#include<bits/stdc++.h>
#define maxn 1000001
using namespace std;
struct kkk{
int key1,key2,index;
}date[maxn];
char s[maxn];
int rk[maxn],sa[maxn],n;
bool cmp(kkk a,kkk b){ //排序方式
if(a.key1==b.key1)return a.key2<b.key2; //第一关键字相同排第二关键字
return a.key1<b.key1; //按第一关键字排序
}
void Suffix_Sort(){
int w,level;
for(int i=0;i<n;i++) rk[i]=s[i]-'0'; //刚开始Rank值赋值
w=1; //w表示长度
while(1){
if(w>n)break; //如果长度越界就break
for(int i=0;i<n;i++){
date[i].index=i; //刚开始标记下标
date[i].key1=rk[i]; //记录第一关键字
if(i+w<n){
date[i].key2=rk[i+w]; //如果没有越界就记录第二关键字
}else{
date[i].key2=-1; //越界就赋一个很小的值
}
}sort(date,date+n,cmp); //快速排序
rk[date[0].index]=level=1; //刚开始的排名是1
for(int i=1;i<n;i++){
if(date[i].key1==date[i-1].key1&&date[i].key2==date[i-1].key2){ //如果一、二关键字相同则排名相同
rk[date[i].index]=level;
}else{
rk[date[i].index]=(++level); //否则就排名++
}
}
if(level==n)break; //如果每一个都不一样就可以break了
w<<=1; //长度增加
}
}
int main(){
scanf("%s",s);
n=strlen(s);
Suffix_Sort();
for(int i=0;i<n;i++) sa[rk[i]-1]=i; //计算SA数组
for(int i=0;i<n;i++){
printf("%d ",sa[i]+1); //输出
}
}
倍增实现————基数排序
倍增的正解————基数排序,可能有些人还没有学过基数排序,这里先讲一些基数排序
基数排序
思路:先按个位将每一个数放入到桶中,然后按顺序取出;按十位将每一个数放入到桶中,然后按顺序取出;……;按最高位将每一个数放入到桶中,然后按顺序取出。这样的时间复杂度就可以降到O(n).但严格来说还是有一些常数的。
来基数排序可视化可以看看基数排序的原理,进去后选最后一个RADIX SORT就是基数排序。
那么我们的排序方法就可以用基数排序来实现。
一个小优化
如果我们把数全部抽出来,然后再排序,常数会比较大,所以有一个小优化可以减少不少的常数,不过难理解。
在这里,sum数组表示Rank[i]数组的前缀和,每一次要填SA数组,就填在sum[rank[i]],然后sum[rank[i]]要减1.
在排第二关键字的时候,按上一次的Rank数组计算出的sum数组来排,要记得判断有没有越界,如果越界直接按顺序排到最前。
排第一关键字时就按第二关键字的sum排就可以了。
//基数排序版
#include<bits/stdc++.h>
#define maxn 1000010
using namespace std;
char s[maxn];
int n,sa[maxn],rank[maxn],newRK[maxn],key2[maxn],sum[maxn];
int level;
void get_sum(int m){ //get sum前缀和
for(int i=0;i<m;i++) sum[i]=0;
for(int i=0;i<n;i++) sum[rank[i]]++;
for(int i=1;i<m;i++) sum[i]+=sum[i-1];
}
bool cmp(int x,int y,int L){ //相同判断
if(rank[x]!=rank[y])return false;
if((x+L>=n&&y+L<n)||(x+L<n&&y+L>=n))return false;
if(x+L>=n&& y+L>=n) return true;
return rank[x+L] == rank[y+L];
}
void Suffix_Sort(){
for(int i=0;i<n;i++) rank[i]=s[i];
get_sum(256);
for(int i=n-1;i>=0;i--)
sa[--sum[rank[i]]]=i;
int w=1,m=max(n,256);
while(w<n){
int p=0;
for(int i=n-w;i<n;i++)key2[p++]=i; //第二关键字越界排前
for(int i=0;i<n;i++)if(sa[i]>=w)key2[p++]=sa[i]-w;//如果当前长度有第一关键字就记录
//以上按第二关键字排序
get_sum(m);
for(int i=n-1;i>=0;i--){
int j=key2[i];
sa[--sum[rank[j]]]=j; //根据第二字排好的顺序再按第一关键字排序
}
//以上按第一关键字排序,直接覆盖之前的sa数组,不需要再开一个key1
newRK[sa[0]]=0;
level=1;
for(int i=1;i<n;i++){
if(cmp(sa[i-1],sa[i],w))
newRK[sa[i]]=level-1;
else
newRK[sa[i]]=level++;
}
for(int i=0;i<n;i++)
rank[i]=newRK[i]; //赋值到Rank数组
//以上计算长度2*w的rank数组
if (level==n)break;
w<<=1;
}
}
int main(){
scanf("%s",s);
n=strlen(s);
Suffix_Sort();
for(int i=0;i<n;i++)printf("%d ",sa[i]+1);
}
后缀数组的应用
最长公共前缀————Height数组
定义Height[i]=Suf(SA[i-1])和Suf(SA[i])的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀,那么对于j和k(Rank[j]<Rank[k]),则有以下性质:
Suf(j)和Suf(k)的最长公共前缀为Height[Rank[j]+1],Height[Rank[j]+2],Height[Rank[j]+3],……,Height[Rank[k]]中的最小值。
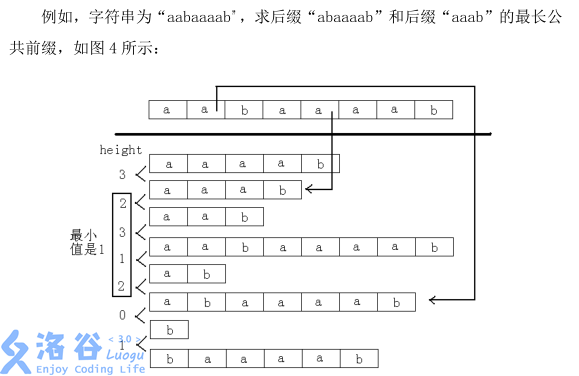
那么现在问题来了如何高效求出Height数组?
求Height数组
暴力做法:
直接对于每一个Height,我们都让它和上一个匹配,那么这样执行n遍,每一次从头开始匹配,时间复杂度为O(n^2).
那么我们可以利用字符串的性质,定义h[i]=Height[Rank[i]],也就是Suf(i)和它前一名的后缀的最长公共前缀
h数组就有以下性质: h[i]>=h[i-1]-1
证明:证明不大重要,重要是记住性质。Suf(k)是排在Suf(i-1)前一名的后缀,则它们的最长公共前缀是h[i-1]。那么Suf(k+1)将排在Suf(i)的前面(这里要求 h[i-1]>1,如果h[i-1]≤1,原式显然成立)并且Suf(k+1)和Suf(i)的最长公共前缀是h[i-1]-1,所以Suf(i)和在它前一名的后缀的最长公共前缀至少是h[i-1]-1。
那么我们根据h数组的性质就可以知道,我们每一次都不需要从头开始匹配,可以从h[i-1]-1位开始匹配,时间复杂度降为O(n).
另外,实现并不需要保存h数组,可以开一个变量计算即可。
代码:
void get_height(){ //求height数组
int k=0;
for(int i=0;i<n;i++){
if(k)k--; //h数组可以直接用一个计数器代替
int j=sa[rank[i]-1];
if(rank[i]-1==-1)continue; //因为我的排名从0开始,所以排名是0时要特判
while(s[i+k]==s[j+k])k++; //从k处找最长公共前缀
height[rank[i]]=k; //记录height数组
}
}
重复子串
可重叠最长重复子串
方法:直接计算出Height数组,取最大值即可,时间复杂度O(n).
不可重叠最长重复子串 POJ 1743
先不考虑转调,马上想到可以二分判断长度为mid是否可行
先求出字符串的height数组,然后在height上分组
每组是height上连续的一段,且其中除第一个以外所有height值都不小于mid(无法满足的就自己单独一个组)
满足这两点的情况下使一组尽量长, 比如这样(图片也出自论文)
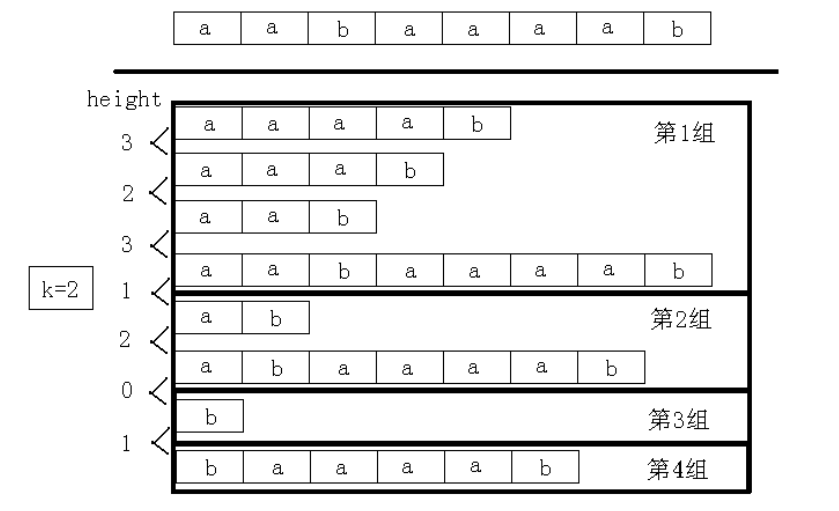
我们只需要检查是否存在一组, 满足其中最大的sa-最小的sa>mid,若满足即可行
因为按这样分组,组内任意两个后缀的lcp长度都不会小于mid
现在考虑转调,其实也很简单
我们只需要在原音乐序列的差分数组上求Height即可
因为若原序列有两个子段的差分序列一样,那么他们一定可以通过加/减同一个数得到
(再次注意转调不是最大的sa-最小的sa+1>mid,因为我们要在原序列的差分数组上求Height)
bool check(int x){ //???
int mx=sa[0],mi=sa[0];
for(int i=1;i<n;i++){
if(height[i]<x)mx=mi=sa[i];
else{
if(sa[i]<mi) mi=sa[i];
if(sa[i]>mx) mx=sa[i];
if(mx-mi>x) return true;
}
}
return false;
}
可重叠的 k 次最长重复子串 POJ 3261
不难想到二分答案,现在我们考虑如何验证。
这里就是后缀数组的一个妙用了。
我们对原串建立后缀数组,观察Height数组。
考虑当前二分出来的mid。如果有至少连续k的Height值都不小
于mid,那么k就是合法的。
故此我们直接扫Height数组看看最长的连续比mid大的Height有多少个即可。
bool check(int x){
int re=-1,now=0;
for(int i=0;i<n;i++){
if(height[i]>=x)now++;
else re=max(re,now),now=1;
}re=max(re,now);
if(re>=k)return true;
else return false;
}




