初探网络流:dinic/EK算法学习笔记
前记
这些是初一暑假的事:
“都快初二了,连网络流都不会,你好菜啊!!!” from 某机房大佬 to 蒟蒻我。
flag:——NOIP后要学网络流
咕咕咕……………………………………………………………………………………
现在是2018-12-29,我终于开始学网络流了。
网络流其实也没有想象的那么难啊,最主要就是要明白怎么建图!!!其他什么的板子一套就完事了。
正式学习
what is 网络流
相信大家都听过网络流这个名字。哦?你知道网络,还知道输入输出流?呀,看来你已经会网络流了啊!
嗯,开个玩笑
网络流(network-flows)是一种图论算法,说起来可能比较抽象,不过我们可以把网络图想象成一个水管分布图,网络流就相当于水流。边就是水管,节点就是一个转换水流的地方。
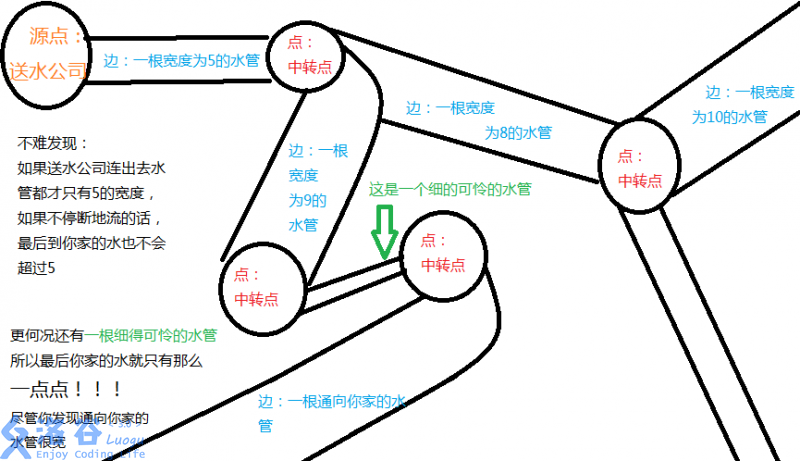
就像上面的图,它其实就是网(shui)络(guan)图,当然,流入你家的可能不止一根水管,那么,如果现在让你分配水怎么流,就是你可以控制水到了某一个点后往哪根水管流,怎么使流入你家的水最多,就是最大流问题。
另外最小割是什么呢?
就是如果有恐怖分子要拆水管,那么他割宽度为5的水管就要相应耗费5单位的力,所以他想耗尽量少的力去让你家没有水,那么他最终耗费的最小的力就是最小割。
网络流的基本性质
1、流量平衡:即 出流的量=入流的量 ,这个比较好理解,就是说如果你入流了100单位水,可水管只能流出50单位水,那么那另外50单位水就爆水管了。
2、最小割=最大流:如果恐怖分子知道你怎么分配使你家的流量最大,那么他就可以把所有水流的路径中最小的割了,那其实就是最大流其中一条路径所能提供的水量。
算法
EK
EK是基于FF算法的一个改良版算法,由于FF算法实在是太废了,我在这里不介绍FF算法,直接讲EK,反正他们的思想差不多。
那么EK算法的思路是什么呢?其实就是不断增广,直到不能再增广为止。那么什么是增广呢,有可能有些人不是很明白?其实增广就是更新,我也一直把增广理解为更新,对一条路进行增广,那条路就是增广路。
额,可能还是不懂吧。其实就是,呐,从源点到汇点不是有很多条路径嘛。EK算法就是每一次抽一条路径,在这条路径上找边权最小值,即这条路径的流量。然后把这条路径的所有边权都减去这个最小值。直到最后没有任何路径可以给汇点输送流量为止。如果一条路径有0容量的边,那么那条路径就废了,因为最多只能流0容量的流量,和不流没区别。
那么我们想一下怎么实现EK算法呢?每一次都进行更新,感觉和搜索有点联系,每一次都向下一个节点更新,直到不能更新就回溯。嗯,那可以写dfs!!!
明显写dfs来跑是非常慢的,这就是FF算法的实现思想。那么EK是什么呢,其实就是把dfs换成了bfs。
那么怎么保证EK的正确性呢?事实上,如果普通建边是跑不了最大流的,EK支持一个反悔操作,什么是反悔呢?不要以为是太高级,其实就是从u走到v,我还可以又从v走回u。我们也可以这么理解,之前有一条路径不可以形成最大流,那么我们就将那条路径反悔,换其他路径。
实现这个反悔操作只需要建反向边,反向边刚开始的流量为0,因为暂时不能往回流,如果流过一条边,那条边的容量自然减少,而反向边容量增加,那么之后反向边就可以流动了。
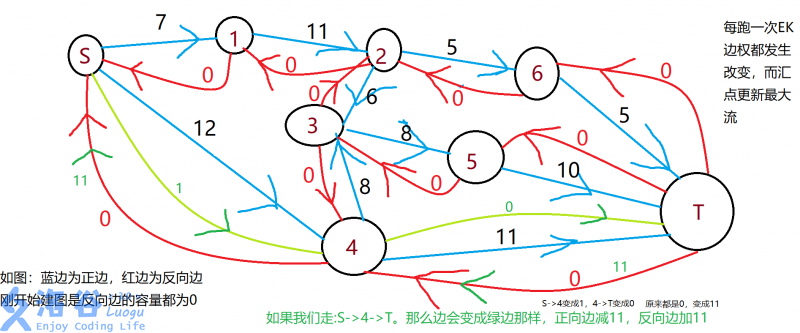
那么来看看EK的具体实现吧:
//网络最大流(EK)
#include<bits/stdc++.h>
#define maxn 1000001
#define INF 119260817
using namespace std;
int cnt,cost[maxn],from[maxn],to[maxn],Next[maxn],head[maxn],consume[maxn];
int dis[maxn],vis[maxn],flow[maxn],last[maxn],maxflow,check;
queue<int>q;
int S,T,n,m;
void add(int x,int y,int z){ //建边
++cnt;cost[cnt]=z;
from[cnt]=x;to[cnt]=y;
Next[cnt]=head[x];head[x]=cnt;
}
bool bfs(int S,int T){ //EK核心代码BFS
for(int i=1;i<=n;i++)last[i]=0,vis[i]=-1;
q.push(S);dis[S]=0;vis[S]=1;flow[S]=INF;
while(!q.empty()){
int u=q.front();q.pop();vis[u]=0;
for(int i=head[u];i!=-1;i=Next[i]){
int v=to[i];
if(cost[i]&&vis[v]==-1){ //发现有路径可以增广
flow[v]=min(flow[u],cost[i]); //流量更新
last[v]=i; //为了最后进行该路径所有边权减最小值,标记来边
q.push(v);
vis[v]=u;
}
}
}if(vis[T]!=-1)return true; //如果汇点没有被更新,那么就结束EK
return false;
}
void update(int S,int T){ //对求出的路径进行更新,即对BFS求出的路径进行减最小值更新
int now=T;
while(now!=S){
int i=last[now];
cost[i]-=flow[T];cost[i^1]+=flow[T]; //记得给反向边增加
now=from[i]; //进行下一条边
}
maxflow+=flow[T]; //最大流加上流量
}
void EK(){
maxflow=0;
while(bfs(S,T)==true){
update(S,T);
}
}
int main(){cnt=1;
memset(head,-1,sizeof(head));
scanf("%d%d%d%d",&n,&m,&S,&T);
for(int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);add(y,x,0); //刚开始要建反向边,容量是0
}
EK();
printf("%d",maxflow);
}
EK时间复杂度:O(n m^2).
dinic
在学dinic之前,希望大家先明白EK的实现思路和原理。讲dinic会在EK的基础上讲的。
其实dinic和EK差不多,只不过dinic多了个分层,这个所谓的分层是一个限制,EK在bfs不是只要有路走就增广吗?而dinic则限制只能往下一层走。
那么来讲讲dinic怎么实现吧:
首先是分层,dinic分层用bfs来分层,这个没什么好说的,就是源点是第0层,和源点有边的点是第1层,这样bfs下去分层。当然,在分层中还可以判断汇点还有没有流可以汇入,如果汇点分不了层了,就代表没有流可以流入汇点了。
然后是找最大流,dinic的找最大流是用dfs的。具体就是从源点找到满足的点就一直递归下去,直到找到汇点,返回中途的最小值,然后更新边权,和EK一样,不过dinic是递归形式,所以可以直接在dfs上更新,不需要在写个update操作。
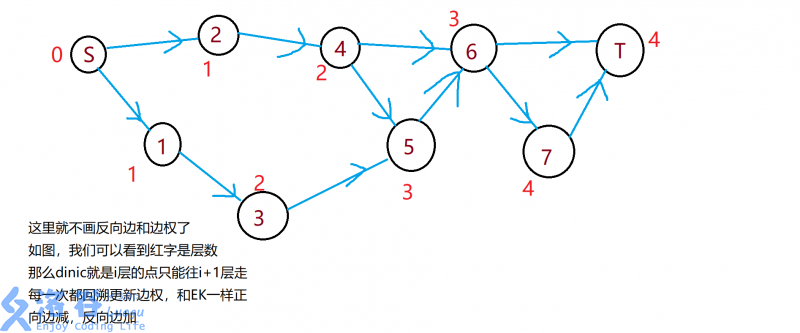
下面看看dinic的实现:
//网络最大流dinic
#include<bits/stdc++.h>
#define maxn 1000001
#define INF 19260817
using namespace std;
int cnt,cost[maxn],from[maxn],to[maxn],Next[maxn],head[maxn];
int level[maxn];
queue<int>q;
int S,T,n,m;
void add(int x,int y,int z){ //建边
++cnt;cost[cnt]=z;
from[cnt]=x;to[cnt]=y;
Next[cnt]=head[x];head[x]=cnt;
}
bool bfs(){ //bfs分层
memset(level,-1,sizeof(level));
level[S]=0;q.push(S);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u];i!=-1;i=Next[i]){
int v=to[i];
if(cost[i]!=0&&level[v]==-1){ //如果容量是0||已被更新就不更新了
level[v]=level[u]+1;
q.push(v);
}
}
}if(level[T]!=-1)return true; //如果流不动了就结束dinic
return false;
}
int dfs(int u,int flow){ //dfs找最大流
if(u==T)return flow;
int ret=flow; //记录初始流量
for(int i=head[u];i!=-1;i=Next[i]){
if(ret<=0)break; //如果已经没流了就退出
int v=to[i];
if(cost[i]!=0&&level[u]+1==level[v]){
int k=dfs(v,min(cost[i],ret)); //把能流的都给下一个点
ret-=k;cost[i]-=k;cost[i^1]+=k; //边权更新,剩余流量更新
}
}
return flow-ret; //返回流出的流量
}
int dinic(){
int ans=0;
while(bfs()==true){
ans+=dfs(S,INF); //累加最大流
}
return ans;
}
int main(){cnt=1;
memset(head,-1,sizeof(head));
scanf("%d%d%d%d",&n,&m,&S,&T);
for(int i=1;i<=m;i++){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);add(y,x,0); //EK一样建边
}
printf("%d",dinic());
}
dinic时间复杂度:O(n^2 m).
希望大家也能学会网络流哦!!!




