P3919 【模板】可持久化数组 -初步探究主席树

本篇blog主要是给自己（大家）看的。

感谢longlongzhu123奆佬（此人初二LCT）的指点，使本蒟蒻可以快速开始主席树入门。

what is 主席树？

$ \ \ \ \ \ \ \ $主席树这个名字只不过是OIer们在思考政(zhe)治(xue)的时候发明的好(du)听(liu)的名字。其实主席树的大名叫“可持久化线段树”，一听这名字就知道主席树很毒瘤，所以他的发明者叫黄嘉泰（hjt* * *(什么鬼啊?)）。

分步理解“可持久化线段树”

$ \ \ \ \ \ \ \ $首先我们先来理解人尽皆知的小名“主席树”，我们可以先看到“主席”这两个字，嗯，很好，很霸气，读起来朗朗上口，所以我们可以知道主席树是一个很霸气的东西，以上扯淡。再来看“树”，从这个字我们可以看出主席树的本质是一棵树，那是一棵什么树，结什么果呢，下面看主席树的大名“可持久化线段树”。

$ \ \ \ \ \ \ \ \(看“可持久化”这四个字，很好理解，主席树十分**持久**，因为它可持久化。那什么叫持久呢，“可持久化”定义：可以支持回退，访问之前版本的数据结构；支持回退操作的意思就是可以访问未经过其他操作的版本，也就是说返回到了以前的版本。那么我们继续看“线段树”这几个字眼，十分熟悉！相信大家肯定学过线段树，如果没学过\)\color{red} \large \text{线段树}$的话，那就可以跳过这篇blog了。我们可以知道主席树是基于线段树的一种数据结构WOW。

$ \ \ \ \ \ \ \ $综上所述，主席树是一种霸气的，持久的，基于线段树的数据结构。

---

主席树基本原理

$ \ \ \ \ \ \ \ $前文说了，线段树与主席树的本质是一样的，只不过主席树可持久化，那么难点就在于怎么支持可持久化。

$ \ \ \ \ \ \ \ $我们想要支持回退操作就可以对每一次修改操作都进行一次复制，将未进行操作的线段树版本进行复制，再对原线段树版本进行修改，那么我们就可以访问到旧版本的线段树了。不过现在问题来了，这样的空间复杂度将会乘上一个m，变成O(n*m)。不用说，肯定会陷入mle中不可自拔。

$ \ \ \ \ \ \ \ $那我们来分析一下单点修改的线段树：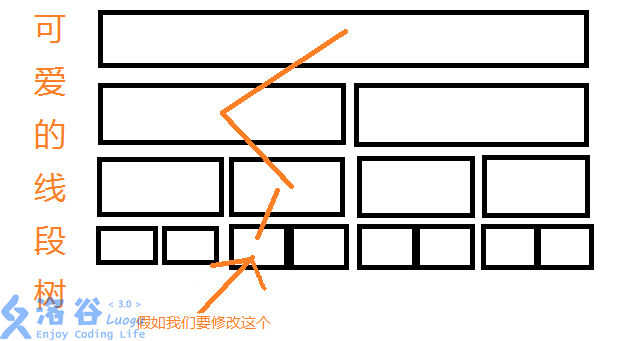

$ \ \ \ \ \ \ \ $我们发现只有橙颜色经过的结点才被修改过。那么我们就可以思考，我们可不可以只对这些节点进行修改呢？答案当然是可以的，主席树的基本思想就是只对进行修改的结点进行复制。那么主席树是长什么样子的呢，下面一起来看一下吧。

$ \ \ \ \ \ \ \ $看着怎么恶心的图，相信大家还是可以发现这个图中主席树的一些性质：

1、每一次修改增加的节点个数为log(n)。

2、增加的非叶子结点会连向一个是其他版本的节点，一个是连向新节点。

3、主席树有很多根……

4、对于每一个根都可以构成一棵完整的线段树。

5、每一个节点都有可能有不只一个爸爸……

$ \ \ \ \ \ \ \ $所以我们可以知道主席树只会对部分节点进行复制，并且每一次复制的节点个数是log(n)。我们每一次想询问一个版本的线段树，就可以在那个版本的根构成的线段树中询问。

但同时也延伸出许多问题：

1、怎么构建新节点？怎么给新节点编号？怎么连边？

2、怎么访问子节点？

3、怎么存根？

$ \ \ \ \ \ \ \ $很明显这些问题在线段树中完全不会出现，我们可以感觉到主席树在建树的代码中会和线段树不同。

现在给出刚才问题的答案：

1、直接开一块内存池存新节点。编号为此时总节点数个数+1。开结构体存子节点编号；线段树建什么边，一指了事。

2、访问子节点编号，不是像线段树一样乘2或乘2+1，而是在结构体存子节点编号。

3、另外开个数组存。

---

代码主要和线段树差不多，下面就看代码吧。

代码 P3919 【模板】可持久化数组

所以我们定义一个节点要存三个信息：左儿子，右儿子，权值

struct kkk{
	int l,r,val;
}tree[maxn];

新建节点：

int clone(int node){
	top++;
	tree[top]=tree[node];//全部信息都传到新节点
	return top;
}

建树其实就是新建节点的过程：

int maketree(int node,int begin,int end){
	node=++top;
	if(begin==end){
		tree[node].val=a[begin];
		return top;
	}
	int mid=(begin+end)>>1;
	tree[node].l=maketree(tree[node].l,begin,mid);
	tree[node].r=maketree(tree[node].r,mid+1,end);
	return node;
}

更新和线段树很像：

int update(int node,int begin,int end,int x,int val){
	node=clone(node);	//更新就要新建节点 
	if(begin==end){
		tree[node].val=val;
	}else{
		int mid=(begin+end)>>1;
		if(x<=mid)
			tree[node].l=update(tree[node].l,begin,mid,x,val);	//访问左子树 
		else
			tree[node].r=update(tree[node].r,mid+1,end,x,val);	//访问右子树 
	}
	return node;
}

询问也一样：

int query(int node,int begin,int end,int x){
	if(begin==end){
		return tree[node].val;
	}else{
		int mid=(begin+end)>>1;
		if(x<=mid)
			return query(tree[node].l,begin,mid,x);	//访问左子树 
		else
			return query(tree[node].r,mid+1,end,x);	//访问右子树 
	}
}

那么主席树的操作部分就写完了QwQ

再来看主程序，里面看根怎么存储：

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	root[0]=maketree(0,1,n);	//root[i]为i版本的根编号，刚开始编号为0 
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&rt,&mode,&x);
		if(mode==1){
			scanf("%d",&y);
			root[i]=update(root[rt],1,n,x,y);	//保存版本 
		}
		else{
			printf("%d\n",query(root[rt],1,n,x));	//输出 
			root[i]=root[rt];					//新建版本 
		}
	}
}

那么这道题就写完了。（其实我觉得一看图就懂了，代码什么的都是假的）