noip2008 双栈排序

题目描述

Tom最近在研究一个有趣的排序问题。如图所示，通过2个栈S1和S2，Tom希望借助以下4种操作实现将输入序列升序排序。

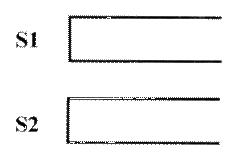
操作a

如果输入序列不为空，将第一个元素压入栈S1

操作b

如果栈S1不为空，将S1栈顶元素弹出至输出序列

操作c

如果输入序列不为空，将第一个元素压入栈S2

操作d

如果栈S2不为空，将S2栈顶元素弹出至输出序列

如果一个1~n的排列P可以通过一系列操作使得输出序列为1，2，…，(n-1)，n，Tom就称P是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”，而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列：<a,c,c,b,a,d,d,b>

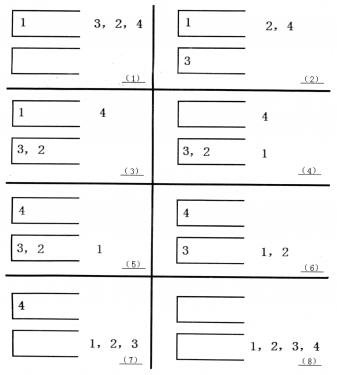
当然，这样的操作序列有可能有几个，对于上例(1,3,2,4)，<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。

输入输出格式

输入格式：

 

输入文件twostack.in的第一行是一个整数n。

第二行有n个用空格隔开的正整数，构成一个1~n的排列。

 

输出格式：

 

输出文件twostack.out共一行，如果输入的排列不是“可双栈排序排列”，输出数字0；否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

 

输入输出样例

输入样例#1：

【输入样例1】
4
1 3 2 4
【输入样例2】
4
2 3 4 1
【输入样例3】
3
2 3 1

输出样例#1：

【输出样例1】
a b a a b b a b
【输出样例2】
0
【输出样例3】
a c a b b d

说明

30%的数据满足： n<=10

50%的数据满足： n<=50

100%的数据满足： n<=1000

/*
说一下这个题的做法吧，他这个题又要字典序最小，又要双栈出入，我们先考虑单栈的情况，单栈在什么情况下不能排序？直觉告诉我们，如果你要一个数字而这个数字又被压在一个更大的数字地下，那么就不行，被压在底下的这个数字肯定是当时不能弹出的，因为比较小的数字还没入栈，形式化的表述为i<j<k且a[j]>a[i]>a[k],那么这种情况就必须要用另一个栈解决了，意即把i,j分在两个栈里，很自然的想法就是二分图染色，至于字典序的问题，只要尽量让一号栈操作就可以了
！！注意那个答案之间是有空格的，一开始在这个sb地方跪了
*/
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<stack>
#define ll long long
using namespace std;
const int maxn = 1005;
int read(){
    int x=0,f=1;
    char ch=getchar();
    while(!(ch>='0'&&ch<='9')){if(ch=='-')f=-1;ch=getchar();};
    while(ch>='0'&&ch<='9'){x=x*10+(ch-'0');ch=getchar();};
    return x*f;
}
struct edge{
    int v;
    int nxt;
}e[maxn*2];
int n,a[maxn],mn[maxn];
int head[maxn],cnt;
int col[maxn],ft;
int vis;
vector<char> ans;
stack<int> aa,bb;
void ins(int u,int v){
    cnt++;
    e[cnt].v = v;
    e[cnt].nxt = head[u];
    head[u] = cnt;
}
bool dfs(int x,int c){
    col[x] = c;
    for(int i = head[x];i;i = e[i].nxt){
        if(col[e[i].v] == c) return false;
        if(!col[e[i].v] && !dfs(e[i].v,3-c)) return false;
    }
    return true;
}
bool get_c(){
    for(int i = 1;i <= n;i++){
        if(!col[i]){
            if(!dfs(i,1)) return false;
        }
    }
    return true;
}
void get_ans(){
    int now = 1;
    while(1){
        if(vis == n) break;
        else if(!aa.empty() && aa.top() == vis + 1){
            vis++;
            aa.pop();
            ans.push_back('b');
        }else if(!bb.empty() && bb.top() == vis + 1){
            vis++;
            bb.pop();
            ans.push_back('d');
        }else if(col[now] == ft){
            aa.push(a[now]);
            now++;
            ans.push_back('a');
        }else if(col[now] != ft){
            bb.push(a[now]);
            now++;
            ans.push_back('c');
        }
    }
    for(int i = 0;i < ans.size();i++){
        putchar(ans[i]);
        putchar(' ');
    }
}
int main(){
    n = read();
    for(int i = 1;i <= n;i++) a[i] = read();
    mn[n] = a[n];
    for(int i = n-1;i >= 1;i--){
        mn[i] = min(mn[i+1],a[i]);
    }
    for(int i = 1;i < n-1;i++){
        for(int j = i + 1;j < n;j++){
            if(a[i] < a[j] && mn[j+1] < a[i]){
                ins(i,j);
                ins(j,i);
            }
        }
    }
    if(!get_c()){
        cout<<0;
        return 0;
    }
    ft = col[1];
    for(int i = 1;i <= n;i++){
        if(!col[i]) col[i] = ft;
    }
    get_ans();
    return 0;
}