Test_1 一元二次方程用例测试以及测试用例
- 代码实现
package com.source;
class Equation {
private double a;
private double b;
private static double c;
Equation(){//无参构造
a = 0;
b = 0;
c = 0;
}
Equation(double a,double b,double c){//有参构造
this.a = a;
this.b = b;
this.c = c;
}
public void setA(double a) {
this.a = a;
}
public double getA() {
return a;
}
public void setB(double b) {
this.b = b;
}
public double getB() {
return b;
}
public void setC(double c) {
this.c = c;
}
public double getC() {
return c;
}
public double getDlt() {//判别式
double result = Math.pow(b, 2)-4*a*c;
return result;
}
private double getRightRoot() {//求解右侧较大实根的方法
double rightRoot = 0;
rightRoot = (-b+Math.sqrt(getDlt()))/(2*a);
return rightRoot;
}
private double getLeftRoot() {//求解左侧较小实根的方法
double LeftRoot = 0;
LeftRoot = (-b-Math.sqrt(getDlt()))/(2*a);
return LeftRoot;
}
public void getRoot() //显示实根或复根,求解
{
if(a == 0)
{
if(b==0)
{
if(c==0)
{//全为0无穷多解
System.out.println("一元二次方程:"+getA()+"x^2+"+getB()+"x+"+getC()+"有无穷多解");
}
else
{
System.out.println("一元二次方程:"+getA()+"x^2+"+getB()+"x+"+getC()+"无解");
}
}
else
{
double result = 0;
result = -getC()/getB();
System.out.println("一元二次方程:"+getA()+"x^2+"+getB()+"x+"+getC()+"唯一解");
}
}//二次系数不为0,两个实根或复根
else
{
if(getDlt() == 0)//判别式为0,有两个相等值
{
double result = 0;
result = -getB()/(2*getA());
System.out.println("一元二次方程:"+getA()+"x^2+"+getB()+"x+"+getC()+"唯一解"+result);
}
else if(getDlt()>0)//两个相异实根
{
System.out.println("一元二次方程:"+getA()+"x^2+"+getB()+"x+"+getC()+"有两个实根:"+
getLeftRoot()+"和"+getRightRoot());
}
else//判别式小于0,有两个复根
{
double imaginaryNumber = 0;
double realNumber = 0;
imaginaryNumber = Math.sqrt(-getDlt())/(2*a);
realNumber = -getB()/(2*a);
System.out.println("一元二次方程:"+getA()+"x^2+"+getB()+"x+"+getC()+"两个复根:"+
realNumber+"i"+"和"+imaginaryNumber+"i");
}
}
}
public static class Test1{
public static void main(String[] args) {
System.out.print("1---");
Equation e1 = new Equation(0,0,0);
e1.getRoot();
System.out.print("2---");
Equation e2 = new Equation(0,0,1);
e2.getRoot();
System.out.print("3---");
Equation e3 = new Equation(0,1,0);
e3.getRoot();
System.out.print("4---");
Equation e4 = new Equation(0,1,1);
e4.getRoot();
System.out.print("5---");
Equation e5 = new Equation(1,2,1);
e5.getRoot();
System.out.print("6---");
Equation e6 = new Equation(1,4,1);
e6.getRoot();
System.out.print("7---");
Equation e7 = new Equation(2,3,3);
e7.getRoot();
}
}
- 测试驱动
public static class Test1{
public static void main(String[] args) {
System.out.print("1---");
Equation e1 = new Equation(0,0,0);
e1.getRoot();
System.out.print("2---");
Equation e2 = new Equation(0,0,1);
e2.getRoot();
System.out.print("3---");
Equation e3 = new Equation(0,1,0);
e3.getRoot();
System.out.print("4---");
Equation e4 = new Equation(0,1,1);
e4.getRoot();
System.out.print("5---");
Equation e5 = new Equation(1,2,1);
e5.getRoot();
System.out.print("6---");
Equation e6 = new Equation(1,4,1);
e6.getRoot();
System.out.print("7---");
Equation e7 = new Equation(2,3,3);
e7.getRoot();
}
}
- bug生成过程
原先的代码是
你生成的错误的bug是分别为:在期望结果是带根号时,实际结果则会转换成小数,无法精确的到数值。
测试用例:
|
序号 |
(a,b,c) |
期望结果 |
实际结果 |
|
|
1 |
(0,0,0) |
无穷解 |
无穷解 |
|
|
2 |
(0,0,1) |
无解 |
无解 |
|
|
3 |
(0,1,0) |
唯一解 X=0 |
唯一解 X=0.0 |
|
|
4 |
(0,1,1) |
唯一解 X=-1 |
唯一解 X=-1.0 |
|
|
5 |
(1,2,1)Dlt=0 |
唯一解 X = -1 |
唯一解 X = -1 |
|
|
6 |
(1,4,1) Dlt > 0 |
两个实根 X1=-2- X2=-2+ |
两个实根 X1=-3.732050807568877 X2=-0.2679491924311228 |
|
|
7 |
(2,3,3) Dlt < 0 |
两个复根 X1=-0.75i X2= |
两个复根 X1=-0.75i X2=0.9682458365518543i |
|
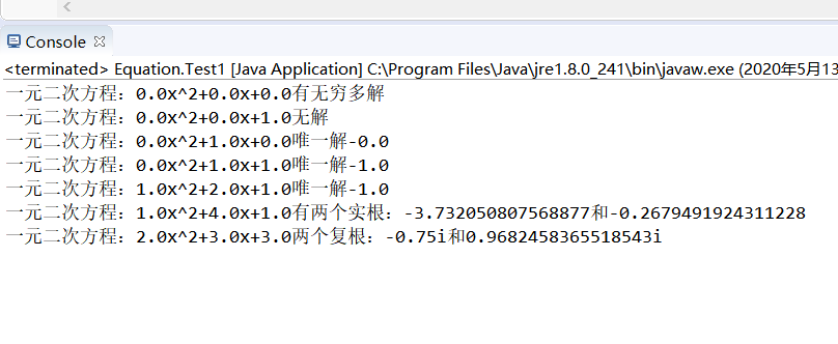
4.结果截图



 浙公网安备 33010602011771号
浙公网安备 33010602011771号