OO第一单元作业总结与心得

第一单元作业总结与心得

目录

• 第一单元作业总结与心得
  • 1. 作业代码复盘与简述
    • 1.1 第一次作业
      • 1.1.1 表达式建模与计算
      • 1.1.2 字符串解析
      • 1.1.3 总体架构
        • 1.1.3.1 总类图
        • 1.1.3.2 类度量
        • 1.1.3.3 方法度量
    • 1.2 第二、三次作业
      • 1.2.1 表达式建模与计算
        • 1.2.1.1 表达式
        • 1.2.1.2 项
        • 1.2.1.3 三角函数
      • 1.2.2 字符串解析
        • 1.2.2.1 字符串的预处理
        • 1.2.2.2 自下而上的解析与合并
        • 1.2.2.3 自定义函数处理
      • 1.2.3 表达式优化
      • 1.2.4 总体架构
        • 1.2.4.1 总类图
        • 1.2.4.2 类度量
        • 1.2.4.3 方法度量
      • 1.2.5 第二次作业到第三次的增量开发
  • 2. bug分析与测试心得
    • 2.1 自我bug分析
      • 2.1.1 bug数量统计
      • 2.1.2 bug成因与反思
    • 2.2 他人bug分析
      • 2.2.1 hack策略
      • 2.2.2 常见bug类型
    • 2.3 测试心得
  • 3. 自我架构总结
    • 3.1 优点总结
    • 3.2 缺点反思
      • 3.2.1 Factor与Expression的重叠
      • 3.2.2 因子处理的冗杂与重复
  • 4. 学习心得体会

1. 作业代码复盘与简述

本人第一单元在第一、二次作业之间进行了一次彻底的重构，而第二、三次作业之间改动之处很少，故此处仅给出第一、三次作业的UML类图与代码度量分析。

1.1 第一次作业

万事开头难，第一次作业在开始展现出来的复杂度是相当唬人的。由于性能分以结果长度为标准给出，不能将本题视作单纯的字符串处理问题，而应该对表达式建模，在逻辑上进行表达式的数学运算。自上而下地考虑，解题的步骤分为两大步（除去IO）：

• 解析字符串，抽象为具体的计算行为

• 对表达式建模，计算得出结果并优化长度

由于第一次作业仅涉及多项式，理论最佳优化方法容易得出，所以题目的难度与复杂度主要集中在第一步上。这里先说明相对简单的第二步。

1.1.1 表达式建模与计算

第一次作业的表达式均为以x为变量的多项式，故只需存储各项的系数与指数即可完整地表示整个表达式。这里给出Expression类的类图。

可以看出，本人选择的系数与指数存储方式是一个Map（作业中具体的容器类型为TreeMap，使输出相对有序），这里Key为指数，Value为系数。需要注意的是Map中系数为0的键值对，它们没有任何意义，应在运算中出现这样的键值对时进行清理。使用Map能够摆脱指数与系数大小的局限性，使大数据与小数据以平等代价存储在表达式中。

数据成员的posId是一个用于输出优化的变量。由于输出的第一项为正时可以减少一个正号的输出，故使用posId记录一个系数为正的项对应的指数（即Key值），输出时优先输出。当各项均为负时，posId为-1。

1.1.2 字符串解析

字符串解析才是这次作业的重点，也是促使本人第二次作业重构的原因。作业发布后关于该问题的解决思路引起了热烈的讨论，同学们与教学团队推荐的主流思路便是递归下降。然而本题细节的处理需要一定技巧（”+“和”-“的归类等），本人在尝试解决无果后转入了一种“放弃思考”的做法。

考虑人脑处理题目所给表达式的步骤：找到括号，识别到表达式因子，找到“**”，识别到幂运算……即按照优先级找到运算符号，再逐级运算化简。这样的思路与建树计算基本相同，但本人选择了更加直观而冗杂的模拟手段。将字符串中的最小元素（如”123“、”**"、")"等）提取出来形成序列，按括号、双星号、星号、正负号的顺序依次遍历搜索，找到对应符号后搜索其影响到的前后文，处理后用处理好的结果替代参与运算的元素存入序列。各层遍历结束后得到表达式结果。

上面提到的元素即Element接口，字符串处理操作封装在Analyser类中，从Analyser类的诸多私有方法可以看到这种做法的笨拙之处。（见总类图）

1.1.3 总体架构

1.1.3.1 总类图

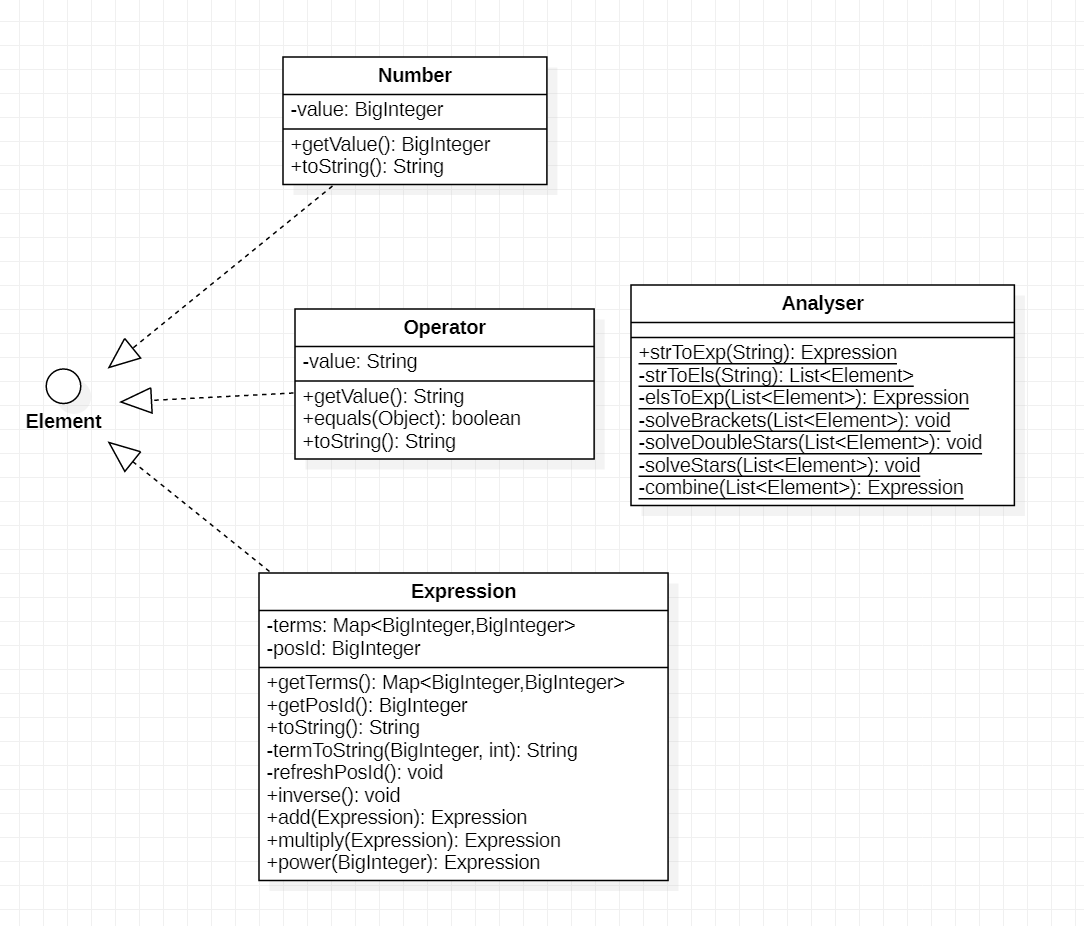
架构思路如1.1.2中所描述的那样，没有什么精妙之处。

1.1.3.2 类度量

Class	OCavg	OCmax	WMC
Analyser	4.428571428571429	8.0	31.0
Expression	3.3636363636363638	10.0	37.0
MainClass	1.0	1.0	1.0
Number	1.0	1.0	3.0
Operator	1.25	2.0	5.0
Total			77.0
Average	2.9615384615384617	4.4	15.4

Analyser类涉及复杂的字符串解析功能，Expression类涉及表达式的计算、输出与优化，因此复杂度较高。

1.1.3.3 方法度量

method	CogC	ev(G)	iv(G)	v(G)
Analyser.elsToExp(List)	0.0	1.0	1.0	1.0
Analyser.strToExp(String)	0.0	1.0	1.0	1.0
Expression.Expression(Expression)	0.0	1.0	1.0	1.0
Expression.getPosId()	0.0	1.0	1.0	1.0
Expression.getTerms()	0.0	1.0	1.0	1.0
MainClass.main(String[])	0.0	1.0	1.0	1.0
Number.Number(BigInteger)	0.0	1.0	1.0	1.0
Number.getValue()	0.0	1.0	1.0	1.0
Number.toString()	0.0	1.0	1.0	1.0
Operator.Operator(String)	0.0	1.0	1.0	1.0
Operator.getValue()	0.0	1.0	1.0	1.0
Operator.toString()	0.0	1.0	1.0	1.0
Expression.inverse()	1.0	1.0	2.0	2.0
Operator.equals(Object)	1.0	2.0	2.0	2.0
Analyser.solveBrackets(List)	3.0	1.0	3.0	3.0
Element.parse(String)	3.0	3.0	2.0	4.0
Expression.refreshPosId()	3.0	3.0	2.0	3.0
Expression.Expression(BigInteger...)	4.0	1.0	3.0	4.0
Expression.add(Expression)	4.0	1.0	3.0	3.0
Expression.power(BigInteger)	4.0	1.0	3.0	3.0
Expression.multiply(Expression)	7.0	1.0	4.0	4.0
Expression.toString()	8.0	1.0	6.0	6.0
Analyser.solveDoubleStars(List)	9.0	1.0	5.0	6.0
Analyser.strToEls(String)	10.0	1.0	7.0	8.0
Analyser.combine(List)	11.0	1.0	7.0	7.0
Analyser.solveStar(List)	17.0	1.0	8.0	9.0
Expression.termToString(BigInteger, int)	18.0	1.0	11.0	11.0
Total	103.0	32.0	80.0	87.0
Average	3.814814814814815	1.1851851851851851	2.962962962962963	3.2222222222222223

可以看到格外复杂的两个函数分别是星号的处理与项的输出。星号处理的前后文比较复杂，尤其是正负号的处理；输出项的函数处理了首项和非首项两种情况，有一定重复部分，可以优化。

1.2 第二、三次作业

经过理论课上老师的强调和作业中要求的细化，本人逐渐掌握了更加面向对象的字符串解析方法。同时，表达式的定义得到了进一步的扩展，多项式的存储方式已经不能表示完整的表达式了。既然解题的两大步骤都发生了巨大的改变，本人果断地选择了重构代码。

另外，引入三角函数后表达式的优化策略已经让人看不到尽头，拥有了无穷无尽的可能性。因此这一节将在上一节的基础之上加入表达式优化的内容。

1.2.1 表达式建模与计算

1.2.1.1 表达式

引入三角函数后，表达式的每一项不再仅仅是x的幂，每一项内三角函数的数量、幂次、类型都不尽相同，一个存储系数与x指数的Map显然无法再完整地展示出表达式的全貌。此时，只有参照表达式的原始定义，用项的序列来表示表达式。

1.2.1.2 项

接下来，建模的工作就转移到了项上。按项的定义，项也可以以因子序列的形式进行存储。但括号展开化简后，项的形式能够呈现出较明显的规律性，于是像第一次作业的表达式一样，可以对项这一层次进行逻辑上的建模。

项的结构与多项式相比更为复杂，主要由以下几个部分组成：

• 系数
• x的幂
• 三角函数的幂

其中三角函数可能不止一个，也可能一个都没有。因此可由两个整数与一个Map存储这些数据。这里给出Term类的类图。

类中refreshed成员和refresh()方法用于控制Map中不存在指数为0的键值对。

1.2.1.3 三角函数

当两个三角函数同为正弦（或余弦）函数且括号内部分等价时，两三角函数应当合并。因此三角函数必须作为一种能够进行比较的对象存储在Map中，表示三角函数的类即是Tri类。

参考上述的三角函数间比较的原则，将三角函数的类型（正弦或余弦）与括号内部分作为Tri类的数据部分。在第二次作业中，括号内部分仅有可能为数字因子或幂函数因子；而在第三次作业中，括号内可能出现任何因子。按照最自然的想法，应用一个Factor对象存储括号内部分，但为了简化最难的表达式因子的处理，本人选择了以Expression对象存储括号内部分。（所有Factor都能够且终将转化为Expression，使得Factor与Expression的职责常发生重叠，这一点将在反思部分中展开讨论）

于是，Expression类也产生了可比较性的需求。又由于Expression由Term序列表示，因此Term之间也必须能够互相比较。Expression

、Term、Tri三类的关系在总类图中有所体现。

1.2.2 字符串解析

重构后的字符串解析开始应用递归下降的思路，按表达式、项、因子三层解析字符串。面对一个表达式，使用正则表达式提取出其中的项，转入项的解析，然后合并得到最终结果；面对一个项，使用正则表达式提取出其中的因子，转入因子的解析，然后合并得到项。（由于因子包含表达式因子、自定义函数因子和求和函数因子，项解析的结果不一定能由一个Term对象表示，故统一解析为Expression对象）

正则表达式的使用是需要技巧的，不进行一些事先处理，正则表达式会难以编写且无法处理括号的嵌套。

1.2.2.1 字符串的预处理

为了方便正则匹配，表达式字符串在进行解析之前需要进行一次预处理。预处理包含三方面：

• 去除所有空白符
• 合并所有相邻的正负号
• 将所有最外层括号替换为方括号

前两项预处理很好理解，也容易证明其正确性（即处理前后表达式合法等价）。最后一项预处理则是为了处理括号的嵌套。合法的表达式中不会出现方括号，因此可以利用方括号对所有的最外层括号进行标识，在正则匹配包含括号的因子时只要匹配一层方括号"\\[[^\\]]*\\]"就行了。

为正确性考虑，字符串的预处理（主要是第三项）最好在每次尝试匹配或识别括号前都进行一次。但这种做法也会留下bug的隐患，bug总结中会展开说明这一点。

预处理函数封装在Expressions类，原本打算作为私有方法由Expressions.parse(String, Factor[])调用，后由于别处的需要改为公有方法。

1.2.2.2 自下而上的解析与合并

Expression类与Term类作为表达式与项的抽象已经做出定义，为了实现因子的解析，本人定义了Factor接口以及实现该接口的Number类、Power类、TriPower类，另外Expression也实现了Factor接口。解析因子时程序先根据字符串内容判断其因子类型，然后转入对应类型的解析函数（见Factors类）。这一部分的内容极其冗杂而不规则，属于这次代码的糟粕部分，将在后文的反思部分展开。

因子解析的结果将返回到项的解析过程中。项在解析前创建一个新的空的Term对象和Expression序列。每解析一个因子，先判断因子的解析结果是否为Expression对象，如果是则加入序列，否则并入Term对象，最后将Term对象与Expression序列中各对象相乘合并。

项解析的结果返回到表达式的解析过程中。Expression对象本质上是Term的序列，在对项解析返回的Expression对象进行合并时涉及到了同类项的合并，同类项的判断函数为Term.similar(Term)。

1.2.2.3 自定义函数处理

自定义函数的引入是第二次作业的一个重大改变，也是容易产生各种bug的棘手需求，需要单独拎出来讨论。本人定义了Function类与Functions类进行相关处理。两类在类图中关系如下：

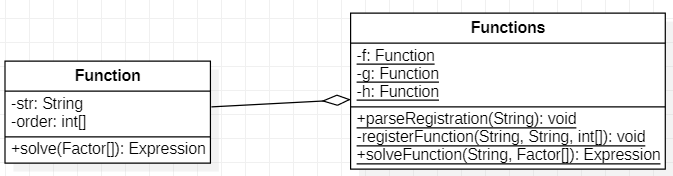
由于题目只涉及f、g、h三个函数，故可以将其定义为Functions类的静态成员。函数的定义与调用都经由Functions类的方法处理，解析过程中不会直接使用Function类。

处理函数的要点在于参数代入。处理这一点时有许多同学选择了一种简单的做法：字符串替换。这很有可能引入无法预料的多种bug，且效率不高，故本人没有采取这种做法。本人采取的做法是在因子解析的过程中进行参数代入。观察类图中涉及“parse”字样的方法（在总类图右侧的各静态方法中），其参数中大都包含一个Factor类的数组。这个数组中的元素分别代表字符串中“x”、“y”、“z”、“i”需要代入的因子（无需代入时元素为null）。因子的解析方法通过这个数组直接对代入的因子进行运算，返回代入后的解析结果。因此所有直接或间接调用因子解析方法的方法都需要在调用时提供这个Factor数组。

为了处理函数定义时形参x、y、z乱序出现的情况（如f(y,x) = ...，g(z) = ...），Function类拥有一个名为order的int数组成员。order[i]表示i号形参（x为0号，y为1号，z为2号）在定义时的位置（-1表示不存在）。如f的定义为f(z,x) = ...，则order = {1,-1,0}。solve方法通过order与传入的Factor数组进行正确的参数代入。

求和因子在代入i时也使用Factor数组。

1.2.3 表达式优化

三角函数的优化可以非常复杂。在第二次作业中，由于三角函数的括号内因子被限制为常数或幂函数，所以优化空间非常局限；但在第三次作业中，各种二倍角优化与平方优化都变得可能了。这方面的优化过于复杂，且三角函数括号内也能够优化，使得优化复杂度几何式地翻倍（如sin(1)**2+cos((sin(x)**2+cos(x)**2))**2），故本人在作业中只实现了一些最基本的优化。此处将其列举出来。

• 括号内为0的优化——sin(0) = 0，cos(0) = 1

• 括号内为负的优化——sin(-A) = -sin(A)，cos(-A) = cos(A)

  只有A中各项均为负时进行优化，故sin((x-1))+sin((1-x))不会优化为0。

• 指数为0时的优化——sin(A)**0 = cos(A)**0 = 1

这些三角函数的优化均在Term对象append一个TriPower对象时进行。

其他与三角函数无关的，与第一次作业一致的优化均得以保留。

1.2.4 总体架构

1.2.4.1 总类图

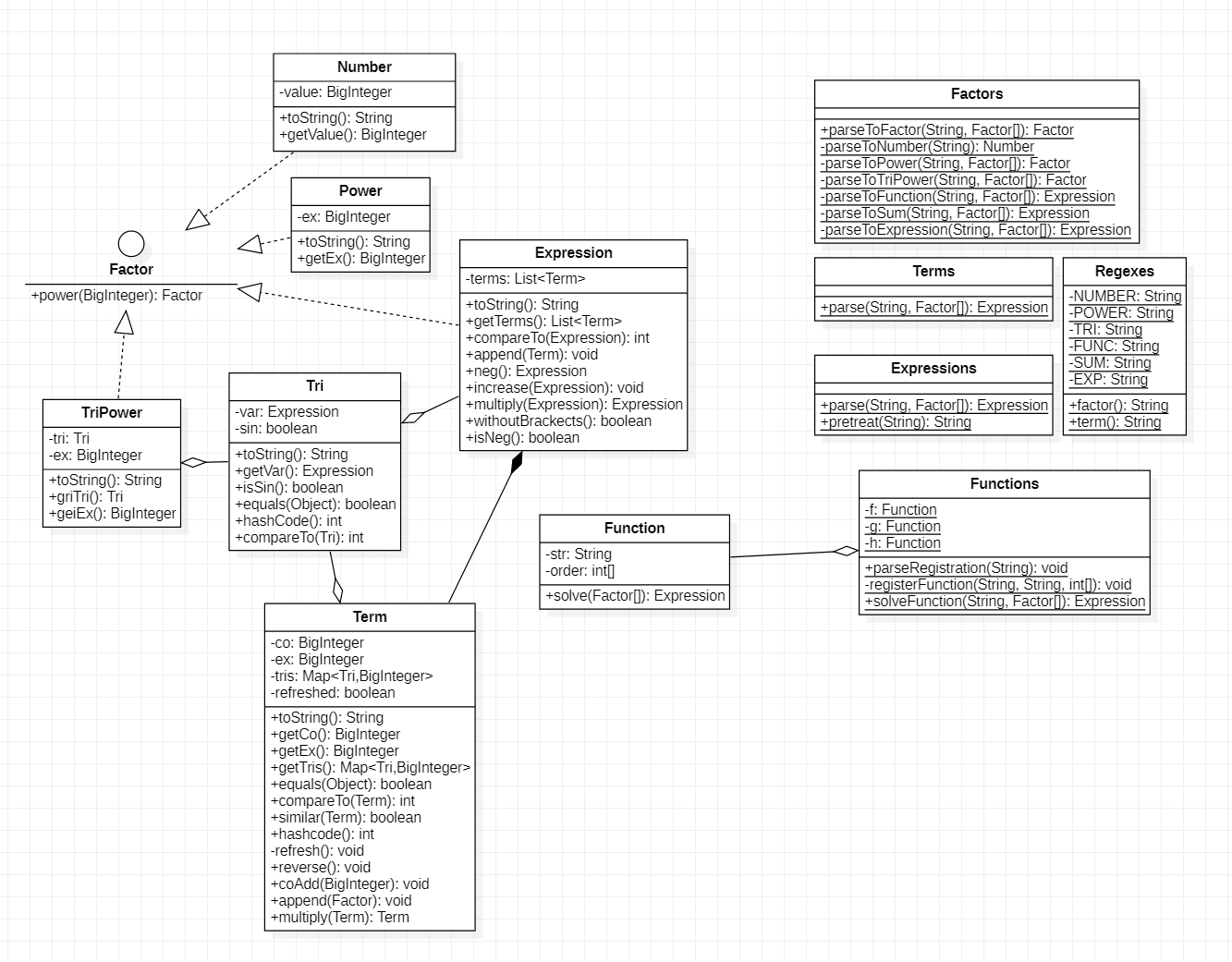
类图左侧为题目概念抽象后得到的数据类型，右侧为任务执行时调用的各种静态方法与数据成员的封装类。

1.2.4.2 类度量

Class	OCavg	OCmax	WMC
Regexes	1.0	1.0	2.0
TriPower	1.2	2.0	6.0
Power	1.25	2.0	5.0
Number	1.5	3.0	6.0
Function	2.0	3.0	4.0
MainClass	2.0	2.0	2.0
Tri	2.142857142857143	5.0	15.0
Term	3.125	13.0	50.0
Expression	3.1666666666666665	8.0	38.0
Factors	3.857142857142857	7.0	27.0
Functions	4.666666666666667	7.0	14.0
Terms	6.0	6.0	6.0
Expressions	6.333333333333333	11.0	19.0
Total			194.0
Average	2.8955223880597014	5.384615384615385	14.923076923076923

Term类与Expression类作为包含各种运算方法的核心类，自然具有较高的WMC。涉及字符串解析的各静态成员封装类自然具有较高的OCavg。

1.2.4.3 方法度量

method	CogC	ev(G)	iv(G)	v(G)
Expression.Expression()	0.0	1.0	1.0	1.0
Expression.Expression(Expression)	0.0	1.0	1.0	1.0
Expression.getTerms()	0.0	1.0	1.0	1.0
Factors.parseToNumber(String)	0.0	1.0	1.0	1.0
Function.Function(String, int...)	0.0	1.0	1.0	1.0
Number.Number(BigInteger)	0.0	1.0	1.0	1.0
Number.getValue()	0.0	1.0	1.0	1.0
Number.toString()	0.0	1.0	1.0	1.0
Power.Power(BigInteger)	0.0	1.0	1.0	1.0
Power.getEx()	0.0	1.0	1.0	1.0
Power.toString()	0.0	1.0	1.0	1.0
Regexes.factor()	0.0	1.0	1.0	1.0
Regexes.term()	0.0	1.0	1.0	1.0
Term.Term()	0.0	1.0	1.0	1.0
Term.Term(BigInteger, BigInteger, Map)	0.0	1.0	1.0	1.0
Term.Term(Term)	0.0	1.0	1.0	1.0
Term.coAdd(BigInteger)	0.0	1.0	1.0	1.0
Term.getCo()	0.0	1.0	1.0	1.0
Term.getEx()	0.0	1.0	1.0	1.0
Term.getTris()	0.0	1.0	1.0	1.0
Term.hashCode()	0.0	1.0	1.0	1.0
Term.reverse()	0.0	1.0	1.0	1.0
Tri.Tri(Expression, boolean)	0.0	1.0	1.0	1.0
Tri.getVar()	0.0	1.0	1.0	1.0
Tri.hashCode()	0.0	1.0	1.0	1.0
Tri.isSin()	0.0	1.0	1.0	1.0
TriPower.TriPower(Tri, BigInteger)	0.0	1.0	1.0	1.0
TriPower.getEx()	0.0	1.0	1.0	1.0
TriPower.getTri()	0.0	1.0	1.0	1.0
TriPower.toString()	0.0	1.0	1.0	1.0
Expression.increase(Expression)	1.0	1.0	2.0	2.0
Expression.neg()	1.0	1.0	2.0	2.0
Expressions.parse(String, Factor[])	1.0	1.0	2.0	2.0
Factors.parseToExpression(String, Factor[])	1.0	1.0	2.0	2.0
Factors.parseToFunction(String, Factor[])	1.0	1.0	2.0	2.0
MainClass.main(String[])	1.0	1.0	2.0	2.0
Power.power(BigInteger)	1.0	2.0	1.0	2.0
Term.similar(Term)	1.0	1.0	2.0	2.0
TriPower.power(BigInteger)	1.0	2.0	1.0	2.0
Expression.power(BigInteger)	2.0	2.0	3.0	3.0
Functions.parseRegistration(String)	2.0	1.0	2.0	3.0
Expression.isNeg()	3.0	3.0	2.0	3.0
Expression.multiply(Expression)	3.0	1.0	3.0	3.0
Functions.registerFunction(String, String, int[])	3.0	1.0	3.0	4.0
Number.power(BigInteger)	3.0	3.0	2.0	4.0
Factors.parseToTriPower(String, Factor[])	4.0	2.0	3.0	4.0
Function.solve(Factor[])	4.0	1.0	1.0	3.0
Term.equals(Object)	4.0	3.0	4.0	6.0
Term.multiply(Term)	4.0	1.0	3.0	3.0
Term.refresh()	4.0	2.0	3.0	4.0
Tri.compareTo(Tri)	4.0	3.0	1.0	5.0
Tri.equals(Object)	4.0	3.0	3.0	5.0
Expressions.parseFromFactor(Factor)	5.0	2.0	4.0	6.0
Factors.parseToFactor(String, Factor[])	6.0	7.0	7.0	7.0
Tri.toString()	6.0	1.0	5.0	6.0
Expression.compareTo(Expression)	7.0	4.0	5.0	6.0
Expression.withoutBrackets()	7.0	4.0	4.0	5.0
Terms.parse(String, Factor[])	7.0	1.0	6.0	6.0
Expression.append(Term)	8.0	3.0	6.0	6.0
Functions.solveFunction(String, Factor[])	9.0	4.0	7.0	7.0
Expression.toString()	10.0	5.0	6.0	8.0
Factors.parseToPower(String, Factor[])	11.0	5.0	3.0	8.0
Factors.parseToSum(String, Factor[])	11.0	2.0	3.0	6.0
Term.compareTo(Term)	11.0	7.0	8.0	9.0
Term.append(Factor)	16.0	1.0	9.0	10.0
Term.toString()	27.0	1.0	13.0	14.0
Expressions.pretreat(String)	35.0	3.0	8.0	15.0
Total	229.0	117.0	173.0	217.0
Average	3.417910447761194	1.7462686567164178	2.582089552238806	3.2388059701492535

复杂的方法基本上都是直接处理字符串的方法，例如字符串的预处理，Expression和Term的toString()。另外就是分支较多，需要对不同Factor类型分别讨论的Term.append(Factor)，Factors.parseToFactor(String, Factor[])一类。

1.2.5 第二次作业到第三次的增量开发

按以上思路进行架构，则两次作业之间区别不大。两次作业的区别主要在于括号内的因子类型得到拓宽，在这个架构下，各种因子类型都能够正确解析，多重函数调用的参数代入也能正确执行，因此不用进行大的修改。

最大的工作量其实在于Tri的改动。1.2.1中提到的用Expression对象存储的括号内因子和Expression、Term、Tri的总体可比较性都是在这次增量开发中实现的。

2. bug分析与测试心得

2.1 自我bug分析

本人这三次作业的成绩呈现出一个逐步上升的态势（这绝不是正常现象吧）。第一次作业强测40分，落入C房；第二次作业强测76.6分，进入B房；第三次作业强测96.9分，荣登A房。除第一次互测被hack了10次以外，第二、三次互测均没有被他人hack到。

2.1.1 bug数量统计

• 第一次作业：强测出错6个点，互测出错10个点，合计16个。bug数2个，但在一次合并修复中修复了（现在说出来不会被追着扣分吧）。
• 第二次作业：强测出错3个点，互测没有出错，合计3个。bug数2个，但只被测到了1个，在一次合并修复中修复。
• 第三次作业：没有出错。

2.1.2 bug成因与反思

本次作业出现的4个bug均为细节处理的bug。现将其列于此处。

• 第一次作业

• • 表达式中系数为0的键值对不会清除，而是以“0”的形式输出。

    (x+1)*(x-1) → x*x0-1

• • 表达式的幂次运算实际为多次自乘。

    (x+1)**3 → 1+4*x+6*x*x+4*x**3+x**4 （自乘两次）

• 第二次作业

• • 字符串预处理可能多次调用，使内层括号也被替换为中括号，导致正则匹配出错。

    f(x) = (sin(x))

    定义语句解析后Function对象f的str成员为[sin(x)]。（第一次预处理）

    解析f(x)因子时转入对[sin(x)]的解析，字符串成为[sin[x]]。（第二次预处理）

    正则匹配时匹配一层方括号，匹配结果为[sin[x]。

• • 进行sin(-A)的优化时忽略其指数。（未被测出）

    sin(-1)**2 → -sin(1)**2

第一次作业的两个bug都非常致命，直接将本人打入C房（C房其他人都没我这么离谱），但需要的改动幅度很小，两个bug正好5行（增3减2）一次合并修复。事实上，这两个bug只要稍微认真一丢丢地去测试就能够很容易地找出来，本人提交作业前仅进行了最小限度的测试，才使得这两个bug得以瞒天过海（中测也没测出来是真的离谱）。

第二次作业的修改幅度也很小。预处理时将中括号也视作最外层括号就能够避免内层括号被替换，三角函数优化额外判断一下指数就行了。预处理的bug比较隐蔽，本人在调试强测测试点时逐条语句地debug才找到了错误原因。优化的bug只是偶然发现罢了，同样属于细节考虑不周。

细节处理的bug可能分布范围很广，无意间留下的概率很高，但可以通过大量且周密的测试有效地找出。本人正是在处理第一单元的作业时忽略了测试的步骤，才使得宝贵的强测分数大量流失。（知道第一次作业只有16人进C房时是真的绷不住了）

由于这些bug的修改幅度极小，且没呈现出什么规律，故其所在方法复杂度也没有分析价值。

2.2 他人bug分析

2.2.1 hack策略

本人对hack的热情不高，故大多情况下采用随机无规律的hack方针。三次作业的hack中，本人首先针对自己在coding中发现的坑点与已知的自己的bug构造数据；然后尝试构建边界情况与其他特殊情况，如0作指数、BigInteger等；最后考虑观察他人代码，针对性地进行hack。

2.2.2 常见bug类型

由于本人没有非常认真地研究他人代码的具体实现，因此这里的类型只根据输入数据与输出数据的特点进行分类。

• 输出格式错误

  x**20 → x*x0（懒人式优化）

  sin((x-2*x)) → sin(-x)（表达式因子缺少括号）

  1-1 → 无输出（输出空串）

• 特殊情况考虑不周

  x**0 → 0或报错 （指数为0）

  sum(i,2,1,i) → 无输出或报错（sum下界大于上界）

  sum(i,10000000000,100000000001,i) → 报错（大整数）

能够留到互测阶段的bug基本都是细节处理的问题，可以通过优质的测试找出。

2.3 测试心得

这几次作业的结果让我清醒地认识到了测试的重要性。然而，测试数据的构建并不是一件容易的事，某种程度上，编写生成测试数据的程序比完成作业本身还要困难。

由于本人在作业过程中没有重视测试，也没有系统化地尝试构建测试数据，因此这方面的经验与知识都有所不足。但考虑到同学们各种细节bug的趋同性，构建特殊情况的数据进行测试应该是比较有效的。另外，构建合法范围内尽可能多样的数据也能更广地揪出藏匿于各处的细节bug。

3. 自我架构总结

这一部分将总结一下本人此次作业架构的优缺点。这里提到的架构当然主要指重构后的架构，但第一次作业的架构也会提到。

3.1 优点总结

这次作业的架构应该比较好地体现出了OO思想。表达式分为三个层次，我们就将这三个层次抽象出来分别建类；因子各有不同，我们分别为其建类，再统一实现因子接口。参见1.2.4.1的总类图，左侧的各类体现了面向对象的思想，右侧的各类则体现了面向过程的思想（一定程度上）。

利用正则表达式匹配字符串中的项和因子，在操作上比较统一，易于理解且缩短了代码长度。正则匹配面临的括号嵌套问题通过最外层括号替换得以解决，解法巧妙而高效。

第一次作业的架构也并非一无是处。按层次进行遍历并搜索前后文进行替换的做法在别的场景应该能够派上用场。

3.2 缺点反思

3.2.1 Factor与Expression的重叠

Expression类实现了Factor接口，而所有Factor又都能向上转化为Expression，这使得两者的职责产生了部分重叠。

Factor接口使得所有不同类型的因子能够得到统一的处理，而架构中对于Factor的处理却基本上都是按类型分别进行的。第一次作业的架构中Element接口不含任何方法，这里的Element用于将不同类型的对象存入同一个容器中。在重构后的架构中，Factor基本也只起到了这样的作用。在这样的情况下，Expression以其统一的处理方式被选作了三角函数、自定义函数与求和函数的因子表示与解析方式。Factor的存在更显尴尬。于是Power、Number、TriPower的存在也尴尬了起来，因为它们都可以视作Expression的特例。

3.2.2 因子处理的冗杂与重复

Factors类中封装的因子解析方法都比较冗杂且内含重复性。这与上一点Factor的细分有关。若在题目要求中新增几类因子，则增量开发的工作量会显得比较大。在这个角度上说，该架构的可拓展性不算很好。

4. 学习心得体会

这个月的OO学习给我留下了很深的印象。

本以为OO的作业内容会像上学期的计组课程一样循序渐进，由浅入深，可第一周的作业就让我连战了一个下午。倒不是说作业的难度曲线太陡，只能说是第一步的步子迈得比较大吧。在这样的冲击下，我忐忑不安地结束了第一周的作业，最后收获了40分的强测分与10次互测的hack。这让我很快调整了心态，正视起了OO这一课程。

由于我在上个学期选修了Java课程，并且自己研究了一阵Java语法与面向对象的coding思维，所以我上手OO假期中的Pre训练与第一次作业都没有遇到太大的困难。但事实证明想要编写正确的代码，经验与细心更加重要。

课程上老师提到的面向对象思维并不难以理解，但将其化为自己的东西是需要多动手多动脑的。OO课程的系统安排着实让我收获了不少，在撰写这篇博文时我的心情也十分愉悦，不知不觉花掉了半天的时间。我现在对第二单元的学习充满期待。

在三次作业一步步收获到更好成绩的过程中，我直观地感受到了自己的成长。最后一次作业在数十次的hack中全身而退，看到自己强测页面一片AC的成就感是难以言表的。

最后感谢课程团队的匠心设计与同学们的互帮互助，愿我们保持这份热情与信念继续前行。