MATLAB卷积运算（conv、conv2、convn）解释
1
conv（向量卷积运算）
所谓两个向量卷积，说白了就是多项式乘法。
比如:p=[1 2 3],q=[1 1]是两个向量，p和q的卷积如下：
把p的元素作为一个多项式的系数，多项式按升幂（或降幂）排列，比如就按升幂吧，写出对应的多项式：1+2x+3x^2;同样的，把q的元素也作为多项式的系数按升幂排列，写出对应的多项式：1+x。
卷积就是“两个多项式相乘取系数”。
（1+2x+3x^2）×（1+x）=1+3x+5x^2+3x^3
所以p和q卷积的结果就是[1 3 5 3]。
记住，当确定是用升幂或是降幂排列后，下面也都要按这个方式排列，否则结果是不对的。
你也可以用matlab试试
p=[1 2 3]
q=[1 1]
conv(p,q)
看看和计算的结果是否相同。
conv2（二维矩阵卷积运算）
a=[1 1 1;1 1 1;1 1 1];
b=[1 1 1;1 1 1;1 1 1];
>> conv2(a,b)
ans =
1 2 3 2 1
2 4 6 4 2
3 6 9 6 3
2 4 6 4 2
1 2 3 2 1
>> conv2(a,b,'valid')
ans =
9
>> conv2(a,b,'same')
ans =
4 6 4
6 9 6
4 6 4
>> conv2(a,b,'full')
ans =
1 2 3 2 1
2 4 6 4 2
3 6 9 6 3
2 4 6 4 2
1 2 3 2 1
convn（n维矩阵卷积运算）
>> a=ones(5,5,5)
a(:,:,1) =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
a(:,:,2) =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
a(:,:,3) =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
a(:,:,4) =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
a(:,:,5) =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
>> b=ones(5,5,5);
>> convn(a,b,'valid')
ans =
125
>> convn(a,b,'same')
ans(:,:,1) =
27 36 45 36 27
36 48 60 48 36
45 60 75 60 45
36 48 60 48 36
27 36 45 36 27
ans(:,:,2) =
36 48 60 48 36
48 64 80 64 48
60 80 100 80 60
48 64 80 64 48
36 48 60 48 36
ans(:,:,3) =
45 60 75 60 45
60 80 100 80 60
75 100 125 100 75
60 80 100 80 60
45 60 75 60 45
2
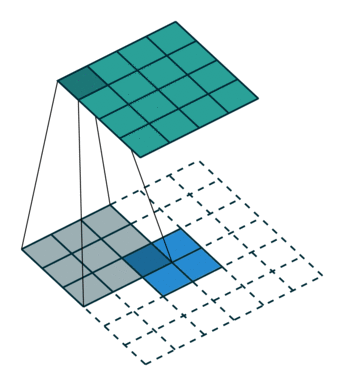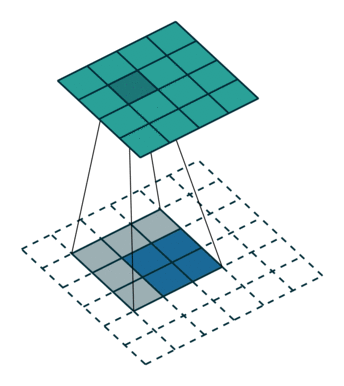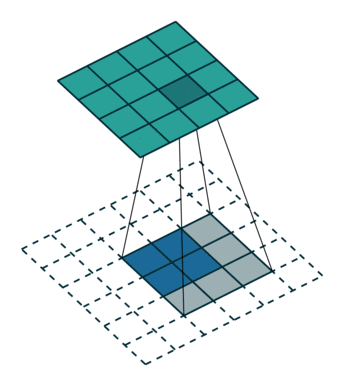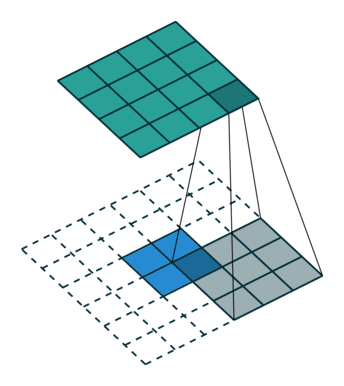
1.full
如下图：
图（1）
图中蓝色为原图像，白色为对应卷积所增加的padding，通常全部为0，绿色是卷积后图片。图的卷积的滑动是从卷积核右下角与图片左上角重叠开始进行卷积，滑动步长为1，卷积核的中心元素对应卷积后图像的像素点。
2.same
如下图：
图（2）
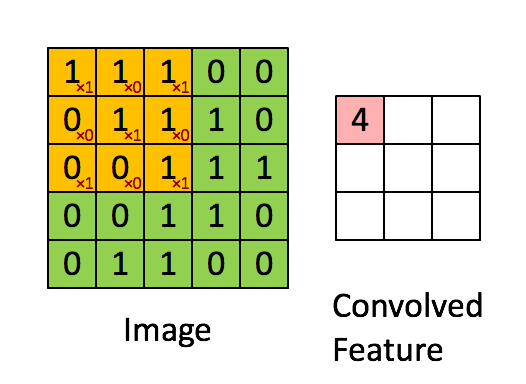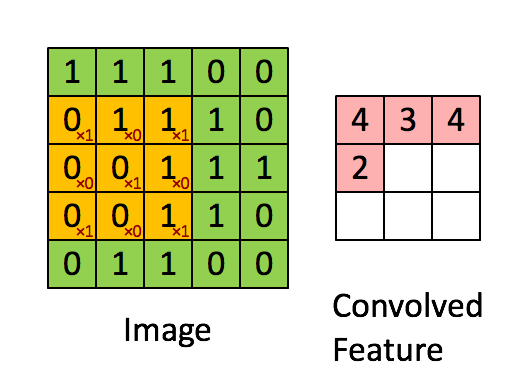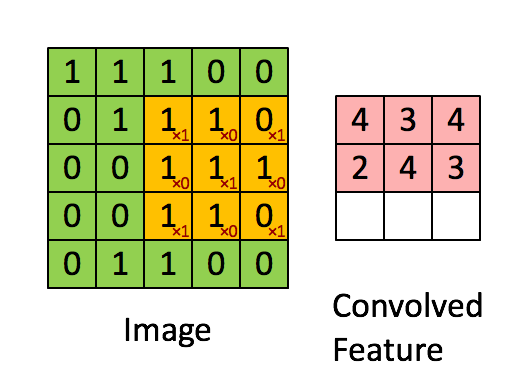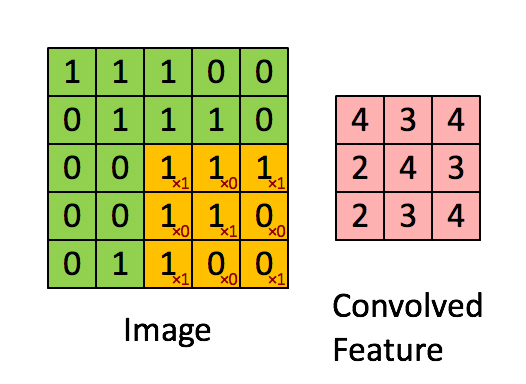
卷积的时候需要对卷积核进行180的旋转，同时卷积核中心与需计算的图像像素对齐，输出结构为中心对齐像素的一个新的像素值
3. valid
如下图：
图（3）
太简单，不解释。
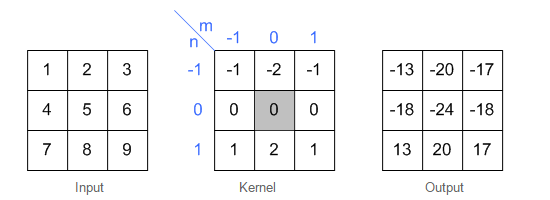
其中，矩阵A和B的尺寸分别为ma*na即mb*nb
① 对矩阵A补零，第一行之前和最后一行之后都补mb-1行，第一列之前和最后一列之后都补nb-1列（注意conv2不支持其他的边界补充选项，函数内部对输入总是补零）；
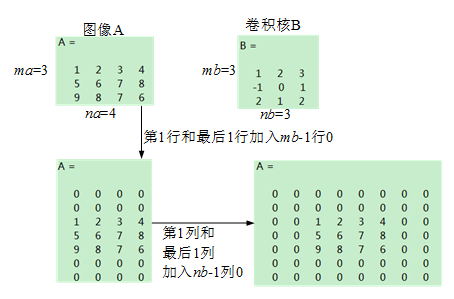
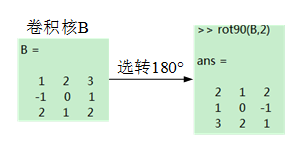
② 将卷积核绕其中心旋转180度；
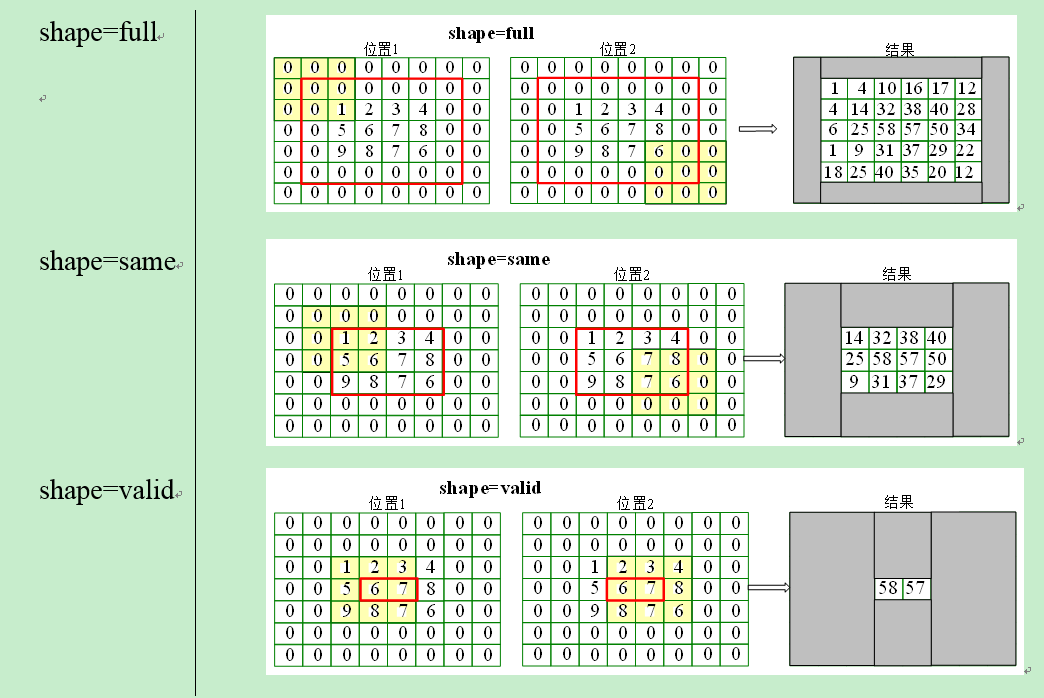
③ 滑动旋转后的卷积核，将卷积核的中心位于图像矩阵的每一个元素，并求乘积和（即将旋转后的卷积核在A上进行滑动，然后对应位置相乘，最后相加）；下面分别是shape=full, same, valid时取输出图像大小的情况，其中：位置1表示输出图像的值从当前核的计算值开始（对应输出图像左上角），位置2表示到该位置结束（对应输出图像右下角）
