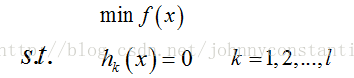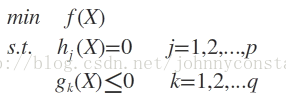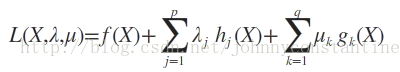深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
转:https://blog.csdn.net/lijil168/article/details/69395023?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.add_param_isCf&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.add_param_isCf
在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件。
我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值(因为最小值与最大值可以很容易转化,即最大值问题可以转化成最小值问题)。提到KKT条件一般会附带的提一下拉格朗日乘子。对学过高等数学的人来说比较拉格朗日乘子应该会有些印象。二者均是求解最优化问题的方法,不同之处在于应用的情形不同。
一般情况下,最优化问题会碰到一下三种情况:
(1)无约束条件
这是最简单的情况,解决方法通常是函数对变量求导,令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。
(2)等式约束条件
设目标函数为f(x),约束条件为h_k(x),形如:
s.t. 表示subject to ,“受限于”的意思,l表示有l个约束条件。
则解决方法是消元法或者拉格朗日法。消元法比较简单不在赘述,这里主要讲拉格朗日法,因为后面提到的KKT条件是对拉格朗日乘子法的一种泛化。
例如给定椭球:
求这个椭球的内接长方体的最大体积。这个问题实际上就是条件极值问题,即在条件 下,求
的最大值。
当然这个问题实际可以先根据条件消去 z (消元法),然后带入转化为无条件极值问题来处理。但是有时候这样做很困难,甚至是做不到的,这时候就需要用拉格朗日乘数法了。
首先定义拉格朗日函数F(x):
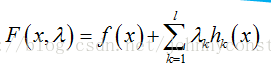
然后解变量的偏导方程:
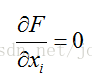
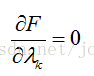
如果有l个约束条件,就应该有l+1个方程。求出的方程组的解就可能是最优化值(高等数学中提到的极值),将结果带回原方程验证就可得到解。
回到上面的题目,通过拉格朗日乘数法将问题转化为
对求偏导得到
联立前面三个方程得到和
,带入第四个方程解之
带入解得最大体积为:
(3)不等式约束条件
设目标函数f(x),不等式约束为g(x),有的教程还会添加上等式约束条件h(x)。此时的约束优化问题描述如下:
则我们定义不等式约束下的拉格朗日函数L,则L表达式为:
其中f(x)是原目标函数,hj(x)是第j个等式约束条件,λj是对应的约束系数,gk是不等式约束,uk是对应的约束系数。
常用的方法是KKT条件,同样地,把所有的不等式约束、等式约束和目标函数全部写为一个式子L(a, b, x)= f(x) + a*g(x)+b*h(x),
KKT条件是说最优值必须满足以下条件:
1)L(a, b, x)对x求导为零;
2)h(x) =0;
3)a*g(x) = 0;
求取这些等式之后就能得到候选最优值。其中第三个式子非常有趣,因为g(x)<=0,如果要满足这个等式,必须a=0或者g(x)=0. 这是SVM的很多重要性质的来源,如支持向量的概念。
接下来主要介绍KKT条件,推导及应用。详细推导过程如下:
????从几何角度看拉格朗日乘子法的物理意义:

该方法适用于约束条件下求极值的问题。对于没有约束的极值问题,显然,如果某一点是极值的必要条件是该点的各方向的偏导数皆为零,也就是说,如果偏导数不全为零,那么就不可能是极值。
例如,一个三元函数w(x,y,z), 它是x,y,z的函数,且在一个约束条件下求它的极值。我们假设图中的曲面就是约束方程g(x,y,z)=0的图像,即约束面。之前没有约束面时,w取极值的必要条件是各个方向偏导数为零,而对于可微函数各个方向偏导为零的充分必要条件是沿x,y,z 方向的偏导为零。现在有了约束面,我们不再需要这么苛刻的必要条件,因为有了约束面,x,y,z在一定程度上被限制了,只能在约束面内移动,因此只需要沿约束面内的各个方向运动时的偏导数(变化化率)为零就可以了,此时自由度由三维下降到两维。满足在约束面内的各个方向偏导为零,也就是说,w取极值的必要条件减弱为待求函数的方向导数(梯度)垂直于约束面,从数学上看,也就是方向导数和约束面的法线方向同向(一个向量等于另一个向量的常数倍),而不需要梯度为零,因为和梯度垂直的方向偏导数一定为零,这样,沿约束面各个方向运动时w的偏导数也就为零了。这便是拉格朗日乘子法求极值的几何意义。
个人总结:
想象一下我们爬山(优化函数)找最高点(求最大值),要想最快的上,要找最陡的方向,陡峭的程度以坡度(方向导数)度量,最陡的方向即为最大坡度(梯度)决定的方向,理想情况下,当无法再上升,坡度(梯度)变成0时,找到最高点(求得最大值)。但是,当我们必须绕圆弧行盘山路爬行时,盘山路(约束条件)约束了我们的路径及方向,我们必须沿着盘山路最陡的方向(梯度,注意此时退化为一维,只有一个方向,为道路切向),当道路不再上升(及切向为0),即找到最高点。
再想想一下我们是海水,从山底向上移动(集体作战),领袖沿着盘山路行进,每一步我们可以找到同海拔的海岸线(等高线),海岸线与盘山路想交,我们可以继续向上移动,直到海岸线与盘山路向切,此时,找到最高海拔,海岸线(等高线)同时与约束方程确定的边界相切。
在极值点,优化函数的等高线、优化函数与约束方程的交线、约束方程的投影线(类似约束曲面的等高线,约束曲线)相切于一点。等高线与约束曲线法向相同(不考虑正负),而优化函数的梯度数值等于其等高线的法向数值,约束方程的梯度数值等于约束曲线的法向数值。故∆f=λ∆g,λ!=0
极值点的2个条件:
1、极值点在优化函数及约束方程上;
2、在极值点,优化函数的等高线、优化函数与约束方程交线、约束曲线相切,优化函数与约束方程交线的梯度(导数)为0
可利用这2个条件求解:
一、根据1将约束方程带入优化函数消元、降维变成无约束低维问题求解,根据2求梯度为0
二、根据2构造似然函数L(X,λ),使在特殊条件下满足1和2,对L(X,λ)解特殊条件。