恢复特征图分辨率的方式对比:反卷积,上池化,上采样
恢复特征图分辨率的方式对比:反卷积,上池化,上采样
文章目录
- 1.(反)卷积-
利用 CNN 做有关图像的任务时,肯定会遇到 需要从低分辨率图像恢复到到高分辨率图像 的问题。解决方法目前无非就是 1)插值,2)反卷积
一般 上采样 (upsamping) 就使用了插值法,包括 “最近邻插值”,“双线性插值”,“双三次插值”。这些方向好比时手工的特征工程,网络是不会对此有任何学习行为的。
如果想要让网络学习如何才能最优地进行上采样,就可以使用 转置卷积,转置卷积没有预先定义好的插值方法,而是具有可学习的参数。
1.(反)卷积
**卷积(Convolution)**的主要目的就是对事物进行特征提取,然后根据特征对其进行识别或决策。而 **反卷积(Deconvolution)**也叫做转置卷积(Transposed Convolution),其目的是恢复特征图的分辨率,一般用于图像分割任务中,需要恢复特征图到原图大小的情况。
(反)卷积原理
假设有一张
4 × 4 4 \times 4 4×4 的输入矩阵(Input),现在要用 3 × 3 3 \times 3 3×3 的卷积核(Kernel)对其进行卷积操作,无 padding,stride 为 1,容易知道输出矩阵(Output)是一个 2 × 2 2 \times 2 2×2 大小的矩阵。卷积输出维度计算公式:
o u t p u t = ( i n p u t + 2 ∗ p − k ) / s + 1 output = (input + 2 * p - k) / s + 1 output=(input+2∗p−k)/s+1其中,input 为输入矩阵的大小,p 为 padding,k 为卷积核大小,s 为卷积步长。根据计算公式可知,卷积后输出大小为
( 4 + 0 − 3 ) / 1 + 1 = 2 (4+0-3)/1+1=2 (4+0−3)/1+1=2。 具体的卷积过程是这样的:<font color="red">Kernel 每次覆盖在 Input 上进行元素级相乘再求和,就得到了 2 × 2 2 \times 2 2×2 Output 上对应位置的输出</font>。 <img src="https://img-blog.csdnimg.cn/20191109212208939.png" alt="在这里插入图片描述"><br> 可以看出,卷积操作是 **“一对多”** 的过程,即 <font color="red">多个值对应一个值</font>,从而达到提取特征的作用。通常卷积操作会使得输入矩阵变小,如果想要保留原尺寸,只需要修改 pad 大小为
P = 1 / 2 ∗ ( k − 1 ) P = 1/2 *(k-1) P=1/2∗(k−1) 即可,通常 pad 的像素值取 0。反过来,我们已经得到了
2 × 2 2 \times 2 2×2 大小的输出矩阵(Output),现在要将其恢复到原本的 4 × 4 4 \times 4 4×4 大小的输入矩阵(Input),这就是让当前矩阵(Output)中的一个值对应到多个值,这就是反卷积。反卷积输出维度计算公式:
o u t p u t = ( i n p u t − 1 ) ∗ s + k − 2 ∗ p output = (input - 1) * s + k - 2 * p output=(input−1)∗s+k−2∗p其中,input 为输入矩阵的大小(此时的 Input 是
2 × 2 2 \times 2 2×2 大小的矩阵,即经过卷积得到的矩阵),p 为 padding,k 为卷积核大小,s 为卷积步长。根据计算公式可知,反卷积后输出大小为 ( 2 − 1 ) ∗ 1 + 3 − 0 = 4 (2-1)*1+3-0=4 (2−1)∗1+3−0=4。<br> <img src="https://img-blog.csdnimg.cn/2019110923053637.png" alt="在这里插入图片描述"><img src="https://img-blog.csdnimg.cn/20191110104156366.gif" alt="在这里插入图片描述">(反)卷积过程
上面卷积核在输入矩阵上不停移动和计算的过程,在实际运算时,其实是将 卷积核重新排列为了 “卷积矩阵”、输入矩阵拉成了一列:如下是
3 × 3 3 \times 3 3×3 的卷积核,将它重排列为 4 × 16 4 \times 16 4×16 的矩阵,空余的地方用 0 来填充。这个 4 × 16 4 \times 16 4×16 是根据输入矩阵的大小决定的,4 表示卷积核会在输入矩阵上进行卷积运算 4 次(也就是每一行都表示一次卷积运算),16 为输入矩阵的数据个数。 输入矩阵 Input 原本是 4 × 4 4 \times 4 4×4 大小的矩阵,现在拉平为一个 16 × 1 16 \times 1 16×1 的列向量,然后将卷积矩阵与输入矩阵的列向量进行相乘,得到 4 × 1 4 \times 1 4×1 的列向量,然后 reshape 到 2 × 2 2 \times 2 2×2,就得到了卷积结果。<br> <img src="https://img-blog.csdnimg.cn/20191110155812111.png" alt="在这里插入图片描述">反卷积就是卷积的逆操作,想要根据得到的
2 × 2 2 \times 2 2×2 大小的输出矩阵恢复到 4 × 4 4 \times 4 4×4 大小的输入矩阵,只需要将 shape 为 4 × 16 4 \times 16 4×16 的 **卷积矩阵 C** 转置一下,得到 shape 为 16 × 4 16 \times 4 16×4 的 **转置卷积矩阵 C.T**,然后用这个转置卷积矩阵与拉成列向量的 2 × 2 2 \times 2 2×2 输出矩阵进行矩阵相乘,就可以得到一个 16 × 1 16 \times 1 16×1 的列向量,同样将它 reshape 到 4 × 4 4 \times 4 4×4 就 OK 啦。 需要注意的是,<font color="red">**反卷积并不能还原出卷积之前的特征图,只能还原出卷积之前特征图的尺寸**</font>。反卷积(Transposed Convolution)在搭建网络时主要有两个作用:
- 像素级分割,需要将图像尺寸恢复到原本的大小;1. 可视化特征,通过反卷积将网络中间层输出的 feature map 还原到像素空间,观察 feature map 对哪些 pattern 响应最大,即卷积结果受到哪部分的影响最大。 # 2. 上池化(Unpooling)
池化(Pooling)操作通常用于将输入特征图缩小一半,达到筛选重要特征的作用。
**上池化(Unpooling)** 是在 CNN 中常用的来表示 max pooling 的逆操作。这是论文《Visualizing and Understanding Convolutional Networks》中产生的思想,下图示意: 反卷积和上池化效果对比:
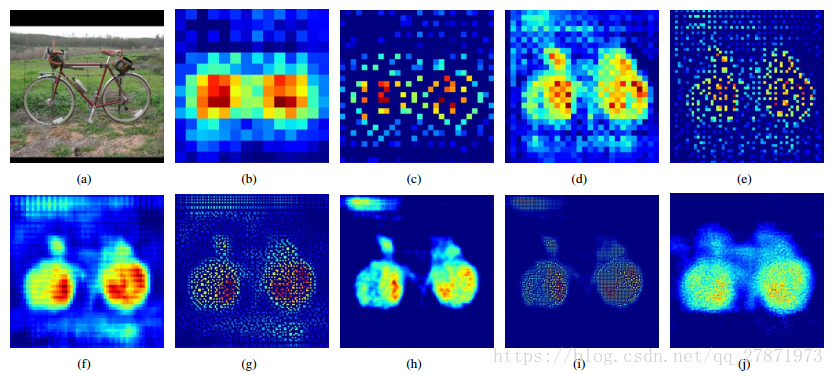
- b,d,f,h,j 为反卷积结果- c,e,g,i 为上池化结果 # 3. 上采样(Upsampling)
在 FCN、U-net 等网络结构中,涉及到了上采样。上采样概念:**上采样指的是任何可以让图像变成更高分辨率的技术**。最简单的方式是 重采样 和 插值:将输入图片进行 rescale 到一个想要的尺寸,并计算每个点的像素值,使用如双线性插值等插值方法对其余点进行插值来完成上采样过程。 对比上采样和上池化的示意图,可以发现区别:
- 上采样(UnSampling)没有使用 MaxPooling 时的位置信息,而是直接通过内容的复制来扩充 Feature Map。- 上池化(UnPooling)过程在 Maxpooling 时保留了最大值的位置信息,之后在上池化时使用该位置信息扩充 Feature Map,除最大值位置以外,其余位置补 0。
参考文章: https://blog.csdn.net/qq_27871973/article/details/82973048
http://www.360doc.com/content/19/0507/12/57110788_834069126.shtml

