斐波那契数列(Fibonacci)(黄金分割)
斐波那契数列(Fibonacci)(黄金分割)
目录:
- 斐波那契数列(Fibonacci)1. 斐波那契数列 与 黄金分割 ##### 一、斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。 指的是这样一个数列:1、1、2、3、5、8、13、21、34、……
程序1………………………………
#include<stdio.h>
#define N 30
int main()
{<!-- -->
int i; // N最大取46
int f[N]={<!-- -->1,1};
for(i=2;i<=N;i++)
f[i]=f[i-2]+f[i-1];
for(i=0;i<N;i++)
{<!-- -->
if(i%5==0) printf("\n"); //第一行 0%0=0 换行
printf("%12d",f[i]);
}
printf("\n");
return 0;
}运行结果……………………………… 程序2………………………………
#include<stdio.h>
#define N 50
int main()
{<!-- -->
int i;
long long int f[N]={<!-- -->1,1};
for(i=2;i<=N;i++)
f[i]=f[i-2]+f[i-1];
for(i=0;i<N;i++)
{<!-- -->
if(i%5==0) printf("\n"); //第一行 0%0=0 换行
printf("%12lld",f[i]);
}
printf("\n");
return 0;
}运行结果………………………………
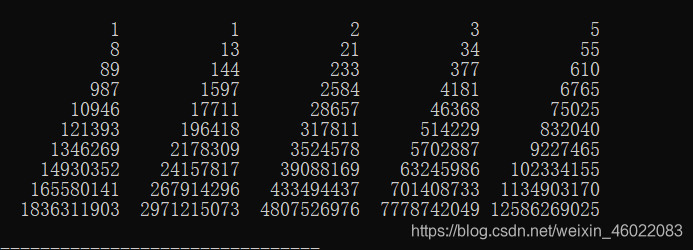
二、Fibonacci与黄金分割
黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618。这个比例被公认为是最能引起美感的比例,因此被称为黄金分割。
数学定义:比值(√5-1):2,近似值为0.618
程序………………………………
#include<stdio.h>
#define N 50
int main()
{<!-- -->
int i;
long long int f[N]={<!-- -->1,1};
for(i=2;i<=N;i++)
f[i]=f[i-2]+f[i-1];
for(i=0;i<N;i++)
{<!-- -->
if(i%5==0) printf("\n"); //第一行 0%0=0 换行
printf("%12lld",f[i]);
}
printf("\n\n");
for(i=0;i<N;i++)
{<!-- -->
printf("%12.6f",1.0*f[i]/f[i+1]);
if(i%5==0) printf("\n");
}
printf("\n");
return 0;
}运行结果………………………………
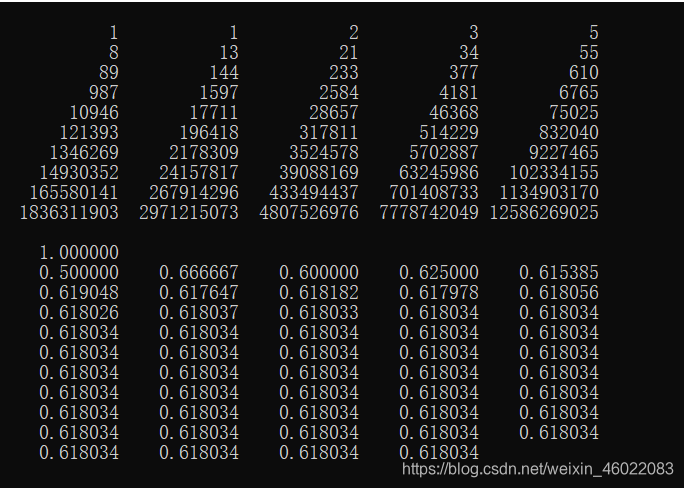


转载于网络 侵权联系作者立即删除QAQ


