树状数组
树状数组
一维树状数组
首先，我们现在需要维护一个一维数组的前缀和，设\(ans[i] = arr[1]+arr[2]+\cdots+arr[i]\)。现在如果我们要修改任意一个元素\(arr[i]\)的值，则相关的前缀和\(ans[i],ans[i+1],\cdots,ans[n]\)都会发生变化。如果我们采用传统的线性顺序扫描求连续数组元素的和，则每次修改\(arr[i]\)后，修整前缀和\(ans[]\)的时间复杂度为\(O(N)\)。若修改数组\(arr[]\)中的元素的次数是\(m\)，则整体前缀和的时间复杂度是\(O(N*M)\)。
为了更好的维护前缀和的效率，这里我们可以是使用树状数组。树状数组通过将线性结构转换为树状结构(线性的只能逐个扫描元素，而树状的可以实现跳跃式的扫面)，使得修改数组元素值后，维护前缀和的时间复杂度为\(O(log_2n)\)，大大的提高了整体的效率。
原理
下面让我们通过一张图来了解树状数组的原理：
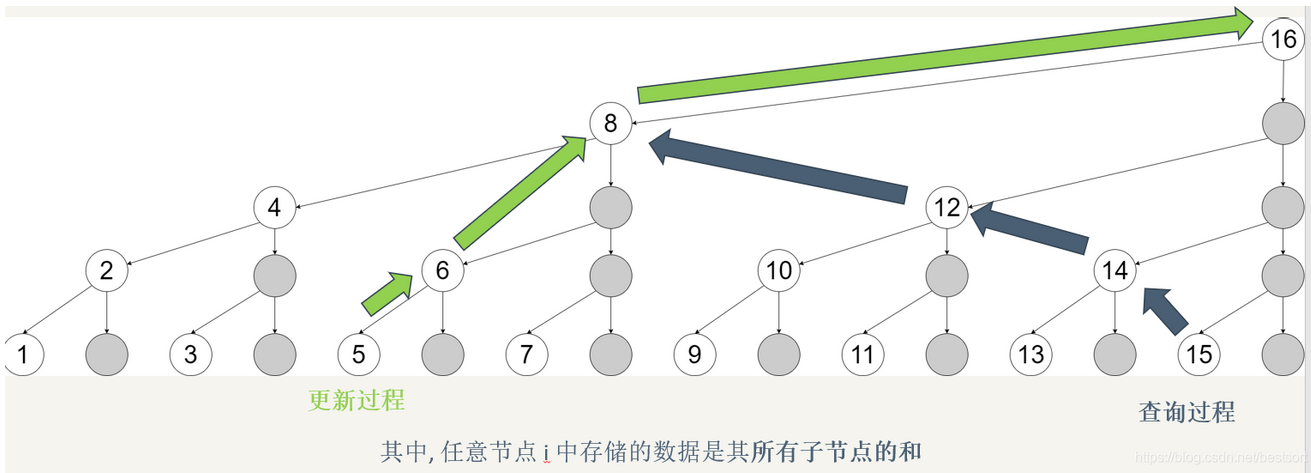
注意：图中的子节点包括自己，例如节点\(8\)，这里面的值是原始数组中\([5,8]\)的和，图中灰色的节点实际上是已被上层覆盖，不再用空间。
下面我们看二进制版本的图：
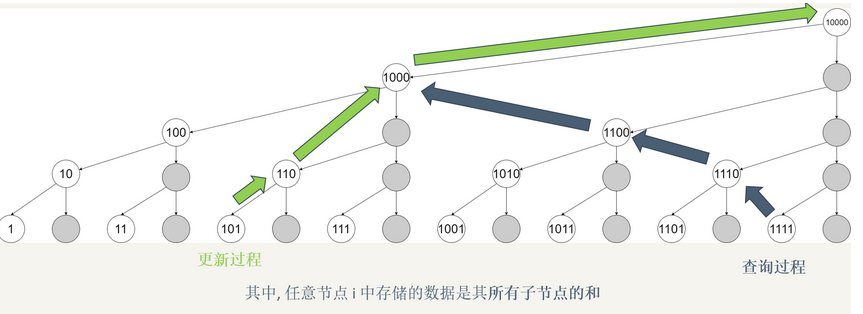
通过第二张图我们可以发现：
更新过程是每次加上二进制中的低位\((101+1\rightarrow 110,110+10\rightarrow 1000 1000+1000\rightarrow 10000)\)。
查询过程是每次减去二进制中的低位\((1111-1\rightarrow 1110,1110-10\rightarrow 1100,1100-100\rightarrow 1000)\)。
那么现在我们怎样来实现这个功能呐？(即怎样寻找一个数的二进制表示中的最低的一位\(1\))，所以我们要在这里了解一个叫做lowbit的函数，顾名思义，lowbit这个函数的功能就是求某一个数的二进制表示中最低的一位1。
具体操作为：
int lowbit(int x){return x & (-x);}
看着是不是极其简单！！！现在让我们来了解这行代码：
我们知道,对于一个数的负数就等于对这个数取反\(+1\)。我们可以以二进制数\(101\)为例，\(101\)的补码为\(010\)，再加上\(1\)就等于\(011\)，最后\(101\)和\(011\)在进行与运算就等于最低位的\(1\)。
其实这个很好理解，原码与补码必然是相反的，负数实在补码的基础上加\(1\)，那么由于进位，负数最末尾的\(1\)和原码最右边的\(1\)一定会在同一个位置。
了解了lowbit函数和树状数组的操作原理之后，我们就可以进行区间查询和单点修改了。
单点修改
现在让我们回到第一张图，如果现在我们要对\(arr[5]\)进行修改(加上\(d\))，则需要进行以下修改：
\(5(101),arr[5] += d\)；
\(5+lowbit(5)=101+1=110=6,arr[6]+=d\)；
\(6+lowbit(6)=110+10=1000=8,arr[8]+=d\)；
\(8+lowbit(8)=1000+1000=10000=16,arr[16]+=d\)；
写成代码就是：
void updata(int x, int b){//x为更新的位置,b为更新后的数,n为数组最大值
while(x <= n){
arr[x] += b;
x += lowbit(x);
}
}
区间查询
其实区间查询就是单点修改的逆操作
例如查询区间\([1,5]\)，\(arr[5]=A[5],arr[4]=A[1]+A[2]+A[3]+A[4]\)；
所以\(getsum(5)=arr[101]+arr[100]\)，\(5-lowbit(5)=101-1=100\)。
写成代码就是：
int getsum(int x){
ll res = 0;
while(x > 0){
res += arr[x];
x -= lowbit(x);
}
return res;
}
二维树状数组
我们已经学会了对于以为树状数组的常规操作，那么我们好奇（谁没事，这么的无聊）能不能把类似的操作放在矩阵上呢？这里我们就来写二维的树状数组。
我们了解了一维树状数组的原理，二维树状数组和一维树状数组类似，在二维树状数组中，\(arr[x][y]\)记录的是右下角为\((x,y)\)，高度为\(lowbit(x)\)，宽度为\(lowbit(y)\)的区间和。
单点修改
void updata(int x, int y, int d){//将点(x, y)加上d
int temp = y;
for(; x <= n; x += lowbit(x)){//当x是固定值时，这就是一个横向的一维树状数组的操作
for(y = temp; y <= n; y += lwbit(y)){//假设y是固定值时，这就是一个竖向的一维树状数组的操作
arr[x][y] += d;
}
}
}
区间查询
int getsum(int x, int y){//求左上角为(1,1)右下角为(x,y) 的矩阵和
int res = 0, temp = y;
for(;x > 0; x -= lowbit(x)){
for(y = temp; y > 0; y -= lowbit(y)){
res += arr[x][y];
}
}
return res;
}
