算法实践：递归思想及其运用

什么是递归？  简单理解就是：自己调用自己

写一个递归函数的关键：1、递归公式 （重复执行某个规则）2、终止条件（也就是最后应该是个常量，而不是一直执行下去）

具体化过程，比如我们要求1~n的整数之和，我们很容易想到这个方式：

 

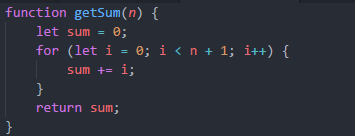
 那么如果换成递归方式去写应该是怎样的呢？

首先我们要找到这个算法的规则，这个和的整数是累加的，也就是它一直在执行累加这个规则（反过来的），终止条件就是n为1的时候。

 

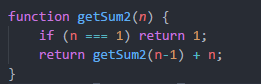
 应用场景：

1、楼梯问题：假如楼梯有n个台阶，每次可以走1个或2个台阶，请问走完这n个台阶有几种走法？

首先需要找到这个算法的规律： getFloor(n) = getFloor(n-1) + getFloor(n-2)

怎么得来的呢？

我们可以知道每步的阶数非1即2，那么可以推出第一步非1即2，如果走1，那就是后面还有getFloor（n-1）种走法，如果是2则有getFloor（n-2）

终止条件也很容易得出：

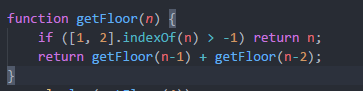
性能优化（使用缓存函数，把计算的结果，存在函数中，当再次调用的时候就可以直接调用，这种方法就是用空间来换取时间）：

 

 

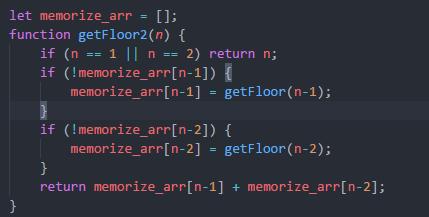
 2、实现对象的深拷贝（内存空间独立，修改拷贝对象，不会改变原来对象的值）

 

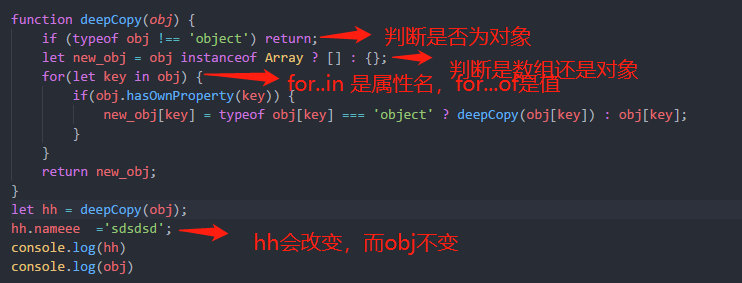
 3、多维数组扁平化（即如何把[1, [2], [3, [4, [5]]]]拍平得到[1,2,3,4,5]）：