利用Multi-Probe LSH构建ANN高维索引

　　感谢大神们的无私奉献精神........因此笔者要坚持开源，专注开源，开源就像在HPU的考试中不像其他人作弊一样，长远来看，会有巨大收获。

一.背景介绍

1.1 相似性搜索简介

　　高维相似性搜索在音频、图形和传感器数据等特征丰富的数据的基于内容的检索中日益重要，一般来说应用在KNN和ANN。

一个针对相似性搜索的理想索引策略应满足如下特性。

　　准确性：返回的结果要和BF返回的结果近似，用查全率表示。

　　时空：查询时间要是o(1)或者o(logn)，空间上不能比源数据还要多，对于大数据，要在主存的容忍范围内，这个我不会定量分析。

　　高维度：高维度下要表现良好。

　　用于KNN的树结构有R、SR、KD、覆盖树和导航网等，这些方法返回的结果准确，但是在高维空间下表现不好，时间上比BF还要慢，正是如此，提出了LSH，LSH的主要思想是将在原始空间中相距近的点以较大的概率映射到同一个桶中，较远点的点精良映射到不同的桶中。具体视线中，为了提高准确率，需要多个哈希表，哈希表数量和数据量是成正比的，大数据下空间效率无法忍受。

1.2 算法背景

　　传统的LSH需要很多哈希表才能保证良好的搜索效率，多探针哈希可以智能地探测可能包含结果的多个桶，该方法受基于熵的LSH的启发（主要是为了降低传统LSH对空间的要求），据评测，时空效率都有提高。

二.LSH简介

　　位置敏感哈希(Locality Sensitive Hashing,LSH)是近似最近邻搜索算法中最流行的一种，它有坚实的理论依据并且在高维数据空间中表现优异。由于网络上相关知识的介绍比较单一，现就LSH的相关算法和技术做一介绍总结，希望能给感兴趣的朋友提供便利，也希望有兴趣的同道中人多交流、多指正。

2.1 LSH原理

　　最近邻问题（nearest neighbor problem）可以定义如下：给定n个对象的集合并建立一个数据结构，当给定任意的要查询对象时，该数据结构返回针对查询对象的最相似的数据集对象。LSH的基本思想是利用多个哈希函数把高维空间中的向量映射到低维空间，利用低维空间的编码来表示高维向量。通过对向量对象进行多次哈希映射，高维向量按照其分布以及自身的特性落入不同哈希表的不同桶中。在理想情况下可以认为在高维空间中位置比较接近的向量对象有很大的概率最终落入同一个桶中，而距离比较远的对象则以很大的概率落入不同的桶中。因此在查询的时候，通过对查询向量进行同样的多次哈希操作，综合多个哈希表中的查询操作得到最终的结果。

　　使用哈希函数对整个数据集进行过滤，得到可能满足查询条件的点再计算距离，这样就避免了查询点与数据集中所有点进行距离计算，提高了查询效率。

2.2 LSH函数族

　　公式不好写。

2.2 LSH索引构建与查找

　　1.索引构建

　　在创建LSH索引时,选取的哈希函数是k个LSH函数的串联函数,这样就相对拉大了距离近的点冲突的概率p1与距离远的点冲突的概率p2之间的差值,但这同时也使这两个值一起减小了,于是需要同时使用L张哈希表来加大p1同时减小p2。通过这样的构造过程,在查询时,与查询点q距离近的点就有很大的概率被取出作为候选近似最近邻点并进行最后的距离计算,而与查询点q距离远的点被当作候选近似最近邻点的概率则很小,从而能够在很短的时间内完成查询。

　　2.查找

　　在L张表中查找相关桶，结果取并集。

三.基于p-stable的LSH的介绍

　　对应海明距离的LSH称为位采样算法（bit sampling），该算法是比较得到的哈希值的海明距离，但是一般距离都是用欧式距离进行度量的，将欧式距离映射到海明空间再比较其的海明距离比较麻烦。于是，研究者提出了基于p-稳定分布的位置敏感哈希算法，可以直接处理欧式距离。

3.1 p-stable分布

　　定义：对于一个实数集R上的分布D，如果存在P>=0，对任何n个实数v1,…,vn和n个满足D分布的变量X1,…,Xn，随机变量ΣiviXi和(Σi|vi|p)1/pX有相同的分布，其中X是服从D分布的一个随机变量，则称D为 一个p稳定分布。
对任何p∈(0,2]存在稳定分布：
　　p=1是柯西分布，概率密度函数为c(x)=1/[π(1+x2)]；
　　p=2时是高斯分布，概率密度函数为g(x)=1/(2π)1/2*e-x^2/2。
　　利用p-stable分布可以有效的近似高维特征向量，并在保证度量距离的同时，对高维特征向量进行降维，其关键思想是，产生一个d维的随机向量a，随机向量a中的每一维随机的、独立的从p-stable分布中产生。对于一个d维的特征向量v，如定义，随机变量a·v具有和(Σi|vi|p)1/pX一样的分布，因此可以用a·v表示向量v来估算||v||p 。

　　笔者认为引入p-stable的原因是为了保距性质（因为LSH的与构建与或构建就相当于降维）。

3.2 基于p-stable哈希函数族

　　p-Stable分布的LSH利用p-Stable的思想，使用它对每一个特征向量v赋予一个哈希值。该哈希函数是局部敏感的，因此如果v1和v2距离很近，它们的哈希值将相同，并被哈希到同一个桶中的概率会很大。
根据p-Stable分布，两个向量v1和v2的映射距离a·v1-a·v2和||v1-v2||pX 的分布是一样的。
a·v将特征向量v映射到实数集R，如果将实轴以宽度w等分，并对每一段进行标号，则a·v落到那个区间，就将此区间标号作为哈希值赋给它，这种方法构造的哈希函数对于两个向量之间的距离具有局部保护作用。

ha,b(v) = floor(a*v+b/w)。

　　b在[0,w]内，其中a*v是点乘（a是行向量），不过具体实现的时候，结合与构建的话，可以吧a*v当做矩阵乘法，a的行数与构建的LSH数目k，就是一锅端了。

3.3 碰撞概率检测

　　随机选取一个哈希函数ha,b(v)，则特征向量v1和v2落在同一桶中的概率该如何计算呢？
首先定义c=||v1-v2||p，fp(t)为p-Stable分布的概率密度函数的绝对值，那么特征向量v1和v2映射到一个随机向量a上的距离是|a·v1-a·v2|<w，即|(v1-v2)·a|<w，根据p-Stable分布的特性,||v1-v2||pX=|cX|<w，其中随机变量X满足p-Stable分布。
可得其碰撞概率p(c):

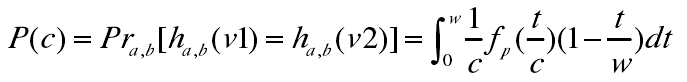
　　根据该式，可以得出两个特征向量的冲突碰撞概率随着距离c的增加而减小。

3.4 相似性搜索

　　经过哈希函数哈希之后，g(v)=(h1(v),…,hk(v))，但将(h1(v),…,hk(v))直接存入哈希表，即占用内存，又不便于查找，为解决此问题，现定义另外两个哈希函数：

　　由于每一个哈希桶（Hash Buckets）gi被映射成Zk，函数h1是普通哈希策略的哈希函数，函数h2用来确定链表中的哈希桶。
　　（1）要在一个链表中存储一个哈希桶gi(v)=(x1,…,xk)时，实际上存的仅仅是h2(x1,…,xk)构造的指纹,而不是存储向量(x1,…,xk)，因此一个哈希桶gi(v)=(x1,…,xk)在链表中的相关信息仅有标识(identifier)指纹h2(x1,…,xk)和桶中的原始数据点。
　　（2）利用哈希函数h2，而不是存储gi(v)=(x1,…,xk)的值有两个原因：首先，用h2(x1,…,xk)构造的指纹可以大大减少哈希桶的存储空间；其次，利用指纹值可以更快的检索哈希表中哈希桶。通过选取一个足够大的值以很大的概率来保证任意在一个链表的两个不同的哈希桶有不同的h2指纹值。

　　注意 就比如你有10000个数据，他们有很多容易被哈希到一起 ，假设期望是10个被哈希到一起 ，那么你表长就取个1000，这个10是个假设，看实际情况定，比如你测试  发现不同的哈希值有n个   那表长控制在1.3n就可以了，正常哈希表要减小冲突 空间利用率都在60-70%之间，其实对于10000个数据点  如果你哈希表长为10000肯定可以装下。实际上这个参数可以事后确定。

3.5 不足与缺陷

　　LSH方法存在两方面的不足：首先是典型的基于概率模型生成索引编码的结果并不稳定。虽然编码位数增加，但是查询准确率的提高确十分缓慢；其次是需要大量的存储空间，不适合于大规模数据的索引。E2LSH方法的目标是保证查询结果的准确率和查全率，并不关注索引结构需要的存储空间的大小。E2LSH使用多个索引空间以及多次哈希表查询，生成的索引文件的大小是原始数据大小的数十倍甚至数百倍。

四.基于熵的LSH简介

4.1 介绍

　　Entopy-based LSH构造索引和基本的LSH策略相似，但是使用了一种不同的查询过程，该方法通过随机生成若干个与查询数据临近的扰动查询数据(perturbing query objects)，将这些数据和待查询数据一同进行哈希，将所有的结果汇总得到候选集。
　　Entopy-based LSH提出的对哈希桶进行采样的方法是，每一次将与查询数据q距离为Rp的随机数据p'进行哈希，得到p'所对应的哈希桶；多次进行这样的采样动作以较高概率保证所有可能的桶都被探测(probe)到。

4.2 不足

　　先，该方法的采样过程效率不足，扰动数据的生成和其哈希值计算速度慢，并且不可避免地得到重复的哈希桶。这样，高概率被映射的桶会多次计算得到，这种计算是浪费的。
另一个缺点是，采样过程需要对近邻距离Rp有一定了解，这对于数据相互以来的情形是困难的。如果Rp过小，扰动查询数据可能无法产生足够的候选集合；如果Rp过大，就需要更多的扰动查询数据来保证更好的查询质量。

五.Multi-Probe LSH算法概述

　　Multi-Probe LSH方法的关键点是，使用一个经过仔细推导出的探测序列(carefully derived probing sequence)，得到和查询数据近似的多个哈希桶。
根据LSH的性质，我们可知如果与查询数据q相近的数据没有和q被映射到同一个桶中，它很有可能被映射到周围的桶中(即两个桶的哈希值只有些许差别),所以该方法的目标是定位这些临近的桶，以便增加查找近邻数据的机会。

• 首先，我们定义一个哈希微扰向量(hash perturbation vector)Δ=(δ1,...,δM)，给定一个查询数据q，基本LSH方法得到的哈希桶是g(q)=(h1(q),...,hM(q))，我们定义微扰Δ，我们可以探测到哈希桶g(q)+Δ。
• • 回想LSH函数
    
    如果我们选择合理的W，那么相似的数据应该映射到相同或者临近的哈希值上（较大的W使得这个值相差最多一个单位），因此，我们关注微扰向量Δ在δi={-1，0，1}

• 微扰向量直接作用于查询数据的哈希值上，避免了Entopy-based LSH方法中扰动数据计算和哈希值计算的天花板问题(overhead)。该方法设计的微扰向量序列(a sequence of pertubation vectors)中，每个向量都映射成一个唯一的哈希值集合，这样就不会重复探测一个哈希桶了。

　　参考文献http://blog.csdn.net/jasonding1354/article/details/44080537

　　扰动序列的产生http://jasonding1354.github.io/2015/03/05/Similarity%20Search/%E3%80%90Similarity-Search%E3%80%91Multi-Probe-LSH%E7%AE%97%E6%B3%95%E6%B7%B1%E5%85%A5/