有线电视网

题目描述

某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构，这棵树的根结点位于足球比赛的现场，树叶为各个用户终端，其他中转站为该树的内部节点。

从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的，一场转播的总费用等于传输信号的费用总和。

现在每个用户都准备了一笔费用想观看这场精彩的足球比赛，有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。

写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。

输入格式

输入文件的第一行包含两个用空格隔开的整数 $N$ 和 $M$，其中 $2\le N\le 3000$，$1\le M\le N-1$，$N$ 为整个有线电视网的结点总数，$M$ 为用户终端的数量。

第一个转播站即树的根结点编号为 $1$，其他的转播站编号为 $2$ 到 $N-M$，用户终端编号为 $N-M+1$ 到 $N$。

接下来的 $N-M$ 行每行表示—个转播站的数据，第 $i+1$ 行表示第 $i$ 个转播站的数据，其格式如下：

$K{A}_1{C}_1{A}_2{C}_2\dots A_k{C}_k$

$K$ 表示该转播站下接 $K$ 个结点（转播站或用户），每个结点对应一对整数 $A$ 与 $C$ ，$A$ 表示结点编号，$C$ 表示从当前转播站传输信号到结点 $A$ 的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。单次传输成本和用户愿意交的费用均不超过 10。

输出格式

输出文件仅一行，包含一个整数，表示上述问题所要求的最大用户数。

样例 #1

样例输入 #1

5 3
2 2 2 5 3
2 3 2 4 3
3 4 2

样例输出 #1

2

提示

样例解释

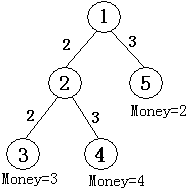
如图所示，共有五个结点。结点 ① 为根结点，即现场直播站，② 为一个中转站，③④⑤ 为用户端，共 $M$ 个，编号从 $N-M+1$ 到 $N$，他们为观看比赛分别准备的钱数为 $3$、$4$、$2$。

从结点 ① 可以传送信号到结点 ②，费用为 $2$；

也可以传送信号到结点 ⑤，费用为 $3$（第二行数据所示）；

从结点 ② 可以传输信号到结点 ③，费用为$2$；

也可传输信号到结点 ④，费用为 $3$（第三行数据所示）。

如果要让所有用户（③④⑤）都能看上比赛，则信号传输的总费用为：$2+3+2+3=10$，大于用户愿意支付的总费用 $3+4+2=9$，有线电视网就亏本了，而只让 ③④ 两个用户看比赛就不亏本了。

题目分析

设状态转移方程dp[i][j]表示以i为根，且当前选择满足j个用户的最大获得费用。
则有dp[i][j]=max(dp[i][j],dp[i][j-k]+dp[t][k]-w[i]);
其中t表示i的某个子树，k表示其中一颗子树t选择满足的用户数，w[i]表示结点i和结点t所连接的边的权值

代码实现

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=3005,M=6005;
int h[N],e[M],ne[M],w[M],idx;
//sum[i]表示以i为根节点的子树中叶子结点的个数 
//dp[i][j]表示以i为根，且当前选择满足j个用户的最大获得费用。 
int dp[N][N],sum[N],n,m;
void add(int x,int y,int z){
	e[idx]=y,w[idx]=z,ne[idx]=h[x],h[x]=idx++;
}
void dfs(int u){
	//如果为叶结点，则叶子结点个数为1 
	if(u>n-m){
		sum[u]=1;
		return;
	}
	for(int i=h[u];~i;i=ne[i]){
		int t=e[i];
		dfs(t);
		//统计以u为根节点的子树中叶子结点的个数 
		sum[u]+=sum[t];
		for(int j=sum[u];j>=0;j--){
			for(int k=0;k<=j&&k<=sum[t];k++){
				dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[t][k]-w[i]);
			}
		}
	}
}
int main(){
	cin>>n>>m;
	memset(h,-1,sizeof h);
	for(int i=1;i<=n-m;i++){
		int k;
		cin>>k;
		while(k--){
			int y,z;
			cin>>y>>z;
			add(i,y,z);
		}
	}
	//初始化 
	for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) dp[i][j] = -1e9;
	//叶子结点只能选择自己一个结点，获得费用即为叶结点本身价值 
	for(int i=n-m+1;i<=n;i++)cin>>dp[i][1];
	dfs(1);
	//从大到小遍历结点1选择满足的用户数，如果费用>=0（即不亏本），则输出能够满足的最大用户数 
	for(int i=sum[1];i>=0;i--){
		if(dp[1][i]>=0){
			cout<<i<<endl;
			break;
		}
	}
	return 0;
}