战略游戏

题目描述

鲍勃喜欢玩电脑游戏，特别是战略游戏，但有时他找不到解决问题的方法，这让他很伤心。
现在他有以下问题。
他必须保护一座中世纪城市，这条城市的道路构成了一棵树。
每个节点上的士兵可以观察到所有和这个点相连的边。
他必须在节点上放置最少数量的士兵，以便他们可以观察到所有的边。
你能帮助他吗？
例如，下面的树：

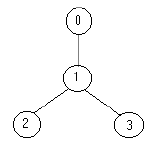
只需要放置 1 名士兵（在节点 1处），就可观察到所有的边。

输入格式

输入包含多组测试数据，每组测试数据用以描述一棵树。
对于每组测试数据，第一行包含整数 N，表示树的节点数目。
接下来 N行，每行按如下方法描述一个节点。
节点编号：(子节点数目) 子节点 子节点 …
节点编号从 0到 N−1，每个节点的子节点数量均不超过 10，每个边在输入数据中只出现一次。

输出格式

对于每组测试数据，输出一个占据一行的结果，表示最少需要的士兵数。

数据范围

0<N≤1500,
一个测试点所有 N相加之和不超过300650。

输入样例

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

输出样例

1
2

题目分析

代码实现

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define int long long
const int N=1505;
int h[N],e[2*N],ne[2*N],idx;
//dp[i][0]表示以i为根节点的树，且当前位置不放士兵的满足条件的最小士兵数
//dp[i][1]表示以i为根节点的树，且当前位置放置士兵的满足条件的最小士兵数
int dp[N][2],vis[N];
void add(int x,int y){
	e[idx]=y,ne[idx]=h[x],h[x]=idx++;
}
void dfs(int u){
    //如果当前位置放置哨兵，则数量为1，否则为0
	dp[u][1]=1,dp[u][0]=0;
	for(int i=h[u];~i;i=ne[i]){
		int j=e[i];
		dfs(j);
		//如果父节点放置了哨兵，则子节点可放可不放，取最小即可
		dp[u][1]+=min(dp[j][1],dp[j][0]);
		//如果父节点没有放置士兵，则子节点必须放置士兵
		dp[u][0]+=dp[j][1];
	}
}
signed main(){
	int n;
	while(cin>>n){
	    //由于有多组测试样例，故每次都需要进行初始化
		int root=-1;
		memset(h,-1,sizeof h);
		memset(vis,0,sizeof vis);
		idx=0;
		for(int i=0;i<n;i++){
			int x,k;
			scanf("%lld:(%lld)",&x,&k);
			while(k--){
				int y;
				cin>>y;
				//建立有向边
				add(x,y);
				//标记以便查找根节点
				vis[y]=1;
			}
		}
		//如果有结点未被标记，则说明其是根节点
		for(int i=0;i<n;i++)if(!vis[i])root=i;
		dfs(root);
		//输出
		cout<<min(dp[root][0],dp[root][1])<<endl;
	}
	return 0;
}