约数之和

题目描述

假设现在有两个自然数 A 和 B，S是 A^B的所有约数之和。
请你求出 S mod 9901 的值是多少。

输入格式

在一行中输入用空格隔开的两个整数 A 和 B。

输出格式

输出一个整数，代表 S mod 9901 的值。

数据范围

0≤A,B≤5×10^7

输入样例

2 3

输出样例

15

注意: A 和 B 不会同时为 0。

题目分析

由于A的约数之和为

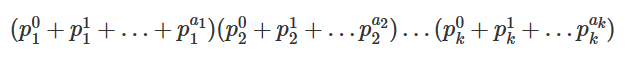
则A^B的约数之和即为

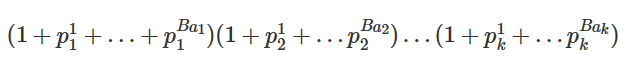
而由于本题B的范围较大，故求解每一项的时候不能直接通过循环求解，故考虑下述方法

这样就可以实现约数之和的计算

代码实现

#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
#define int long long
const int mod=9901;
unordered_map<int,int>mp;
int quick(int a,int b){
	int res=1;
	while(b){
		if(b&1)res=res*a%mod;
		a=a*a%mod;
		b>>=1;
	}
	return res;
}
int sum(int p,int k){
	if(k==1)return 1;
	if(k%2==0)return (quick(p,k/2)+1)*sum(p,k/2)%mod;
	else return (quick(p,k-1)+sum(p,k-1))%mod;
}
signed main(){
	int a,b;
	cin>>a>>b;
	if(a==0)cout<<"0"<<endl;
	else{
		//求因子
		for(int i=2;i<=a/i;i++){
			while(a%i==0){
				mp[i]++;
				a/=i;	
			}
		}
		if(a>1)mp[a]++;
		//计算约数和
		int res=1;
		for(auto t:mp){
			int temp=(t.second*b+1);
			res=res*sum(t.first,temp)%mod;
		} 
		cout<<res%mod<<endl;
	}
	return 0;
}