1053 等重路径
给定一个非空的树,树根为 R。
树中每个节点 Ti 的权重为 Wi。
从 R 到 L 的路径权重定义为从根节点 R 到任何叶节点 L 的路径中包含的所有节点的权重之和。
现在给定一个加权树以及一个给定权重数字,请你找出树中所有的权重等于该数字的路径(必须从根节点到叶节点)。
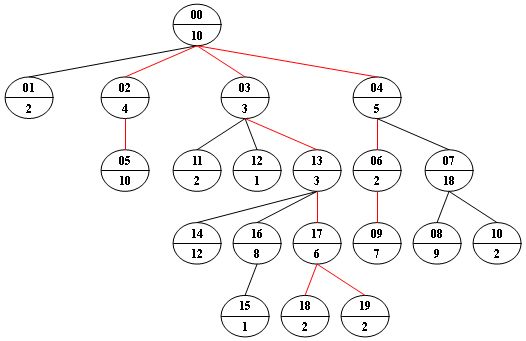
例如,我们考虑下图的树,对于每个节点,上方的数字是节点 ID,它是两位数字,而下方的数字是该节点的权重。
假设给定数为 24,则存在 4 个具有相同给定权重的不同路径:{10 5 2 7},{10 4 10},{10 3 3 6 2},{10 3 3 6 2}, 已经在图中用红色标出。
输入格式
第一行包含三个整数 N,M,S,分别表示树的总节点数量,非叶子节点数量,给定权重数字。
第二行包含 N 个整数 Wi,表示每个节点的权重。
接下来 M 行,每行的格式为:
ID K ID[1] ID[2] ... ID[K]ID 是一个两位数字,表示一个非叶子结点编号,K 是一个整数,表示它的子结点数,接下来的 K 个 ID[i] 也是两位数字,表示一个子结点的编号。
出于方便考虑,根节点固定为 00,且树中所有节点的编号为 00∼N−1。
输出格式
以单调递减的顺序输出所有权重为S的路径。
每个路径占一行,从根节点到叶节点按顺序输出每个节点的权重。
注意:我们称 A 序列 {A1,A2,…,An} 大于 B 序列 {B1,B2,…,Bm},当且仅当存在一个整数 k,1≤k<min(n,m),对于所有 1≤i≤k,Ai=Bi 成立,并且 Ak+1>Bk+1。
数据范围
1≤N≤100
0≤M<N,
0<S<230,
0<Wi<1000
输入样例:
20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19输出样例:
10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2代码实现:
#include<iostream>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
const int N=105;
vector<int>v[N];
vector<string>res;
vector<vector<int> >res1;
int n,m,S,w[N];
bool cmp(vector<int>a,vector<int>b){
for(int i=0;i<a.size()&&i<b.size();i++){
if(a[i]!=b[i])return a[i]>b[i];
}
return a.size()>b.size();
}
struct node{
int x;
vector<int>v1;
int dis;
};
void bfs(int x){
queue<node>q;
vector<int>v1;
v1.push_back(x);
node n1={x,v1,w[x]};
q.push(n1);
while(q.size()){
node n2=q.front();
q.pop();
if(n2.dis==S&&v[n2.x].size()==0){
vector<int>v3;
for(int i=0;i<n2.v1.size();i++)v3.push_back(w[n2.v1[i]]);
res1.push_back(v3);
continue;
}
for(int i=0;i<v[n2.x].size();i++){
vector<int>v2=n2.v1;
v2.push_back(v[n2.x][i]);
node n3={v[n2.x][i],v2,n2.dis+w[v[n2.x][i]]};
q.push(n3);
}
}
}
int main(){
cin>>n>>m>>S;
for(int i=0;i<n;i++)cin>>w[i];
while(m--){
string x;
int k;
cin>>x>>k;
while(k--){
string y;
cin>>y;
v[stoi(x)].push_back(stoi(y));
}
}
bfs(0);
sort(res1.begin(),res1.end(),cmp);
for(int i=0;i<res1.size();i++){
for(int j=0;j<res1[i].size();j++){
if(j==0)cout<<res1[i][j];
else cout<<" "<<res1[i][j];
}
cout<<endl;
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· winform 绘制太阳,地球,月球 运作规律
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人