7-10 红豆生南国

有诗云：

    相思 （王维  唐）
        
红豆生南国， 春来发几枝。

愿君多采撷， 此物最相思。

那么，我们来采红豆吧！

假设红豆树是这个样子的：

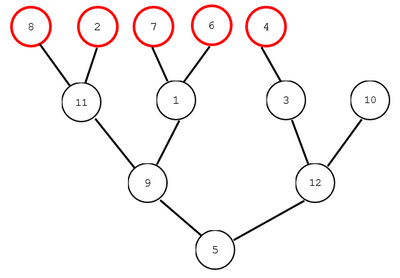
这种红豆树的特点是：

• 每个结点都有一个正整数编号，标在结点内部。结点的编号各不相同。
• 最上方一层结点是 “红豆”（图中红圈所示的5个结点），这一层被称之为红豆层。
• 树的根结点、左子结点、右子结点、左子树、右子树等的定义与“数据结构”中的“二叉树”相同，但它毕竟是“自然界中的树”，树根在最下方，如图中的结点5
• 图中这棵红豆树是“完全二叉红豆树”，类似“数据结构”中的“完全二叉树”。（“完全二叉树”的定义：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是完美二叉树。对于一个有N个结点的二叉树，若其结点对应于相同深度完美二叉树的层序遍历的前 N 个结点，这样的树就是完全二叉树） 从图上看，就是：要么每一层（包括红豆层）的结点数达到最大值，要么只在红豆层的最右边缺少一些结点。

对于红豆树，我们定义两种遍历顺序：

1. 正序遍历：先访问树根结点，再正序遍历其左子树，最后正序遍历其右子树
2. 逆序遍历：先逆序遍历其右子树，再逆序遍历其左子树，最后访问树根结点

对于给定的一棵完全二叉红豆树以及一些要采撷的结点，计算每次采撷能采到的红豆数量。

注意：我们采的点，可能是红豆，也可能不是红豆。采撷一个结点的意思是，把这个结点及这个结点的子树的全部结点从树中采下来。

例如：若采结点7，这是红豆结点，我们将获得1颗红豆；若采结点11，这不是红豆结点（而是一个枝结点！），我们将获得红豆树的一枝，包含2个红豆结点（8和2）。

输入格式:

输入有四行。

第一行是一个不超过60的正整数N，表示完全二叉红豆树中的结点数量。

第二行是N个不超过1000的结点编号序列，以空格间隔，表示的是这棵树的逆序遍历序列。

第三行是一个不超过N的正整数K，表示进行K次采撷。

第四行是K个正整数，依次表示每次要采的结点编号。

输出格式:

输出包含K+1行，

前K行，对于输入的每个采撷的点，在一行输出相应获得的红豆数量。如果这个点已经被采掉了，则输出Zao Jiu Cai Diao Le!。如果这个点在原树中根本不存在，则输出Kan Qing Chu Le?。

最后一行，输出采撷结束之后，这棵红豆树的正序遍历序列，用空格分隔，最后一个结点之后没有空格。如果采撷结束之后树已空，则输出Kong Le!

输入样例1:

对于题目中给出的图，对应的输入是：

12
10 4 3 12 6 7 1 2 8 11 9 5
4
15 12 11 2

输出样例1:

Kan Qing Chu Le?
1
2
Zao Jiu Cai Diao Le!
5 9 1 7 6

输入样例2:

对于题目中给出的图，对应的输入是：

12
10 4 3 12 6 7 1 2 8 11 9 5
1
5

输出样例2:

5
Kong Le!

 

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

 

代码实现：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
#include<vector>
using namespace std;
const int N=105;
int a[N],b[N],vis[N],idx,n;
unordered_map<int,int>mp;
vector<int>v;
//根据完全二叉树下标性质获取每一层的下一层起始下标 
int getLevel(int x){
    if(x==1)return 2;
    else if(x<4)return 4;
    else if(x<8)return 8;
    else if(x<16)return 16;
    else if(x<32)return 32;
    else if(x<64)return 64;
}
void build(int k){
	//如果当前结点下标超过n则直接返回，因为只有n个结点 
    if(k>n)return;
    //遍历左子树 
    build(k*2+1);
    //遍历右子树 
    build(k*2);
    //将当前结点的值设置为逆序遍历的值（由于是逆序遍历，故该行代码应该放在遍历左右子树之后） 
    b[k]=a[idx++];
    //将当前结点的值映射到当前的结点下标，以便根据结点值快速定位结点下标 
    mp[b[k]]=k;
}
int dfs(int x){
	//用res存储结点x下的红豆数 
    int res=0;
    //如果当前结点未被访问过且其为最后一层的叶子结点，则标记该结点为访问过，该叶子结点是个红豆，并返回红豆数量1 
    if(2*x>=getLevel(n)&&x<=n&&!vis[x]){
        vis[x]=1;
        return 1;
    }
    //标记结点为访问过
    vis[x]=1;
    //如果左儿子存在且未被采摘过，遍历左儿子，res加上左儿子的红豆数量 
    if(x*2<=n&&!vis[x*2])res+=dfs(x*2);
    //如果右儿子存在且未被采摘过，遍历右儿子，res加上右儿子的红豆数量 
    if(x*2+1<=n&&!vis[x*2+1])res+=dfs(x*2+1);
    //返回结点x的红豆数 
    return res;
}
void dfs1(int x){
	//如果当前结点下标超过n，则直接返回 
	//或者当前结点已经被采摘过了，那么其子节点一定被采摘掉了，故直接返回，无需继续遍历 
    if(x>n||vis[x])return;
    //存储正序遍历 
    v.push_back(b[x]);
    //遍历左子树 
    dfs1(x*2);
    //遍历右子树 
    dfs1(x*2+1);
}
int main(){
	//n表示结点的数量 
    cin>>n;
    //a数组用于存储红豆树的逆序遍历 
    for(int i=0;i<n;i++)cin>>a[i];
    //根据完全二叉树的性质建树，根节点下标为1
	//完全二叉树的性质：x结点左子树下标为2*x，右子树结点下标为2*x+1 
    build(1);
    int k;
    cin>>k;
    while(k--){
        int x;
        cin>>x;
        //如果当前结点不存在则输出Kan Qing Chu Le?
        if(!mp[x])cout<<"Kan Qing Chu Le?"<<endl;
        //如果当前结点已经被访问过了（即已经被采摘了），则输出Zao Jiu Cai Diao Le! 
        else if(vis[mp[x]])cout<<"Zao Jiu Cai Diao Le!"<<endl;
        else{
        	//利用dfs计算当前结点下的红豆数量 
            int res=dfs(mp[x]);
            cout<<res<<endl;
        }
    }
    //正序遍历一遍红豆树，并将正序遍历结果存下来 
    dfs1(1);
    //如果没有任何结点未被访问过，即采撷结束之后树已空，则输出Kong Le! 
    if(v.size()==0)cout<<"Kong Le!"<<endl;
    else{
    	//输出正序遍历结果 
        for(int i=0;i<v.size();i++){
            if(i==0)cout<<v[i];
            else cout<<" "<<v[i];
        }
    }
    return 0;
}