组合数学基础（卡特兰数）

卡特兰数公式：

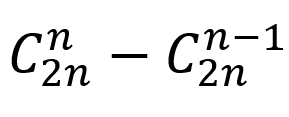或者

引例1、（姐妹洗碗问题）

思考过程：

横坐标表示姐姐洗完的碗的个数，纵坐标表示妹妹摞碗的个数，前提条件为妹妹摞碗的个数不能超过姐姐洗完的碗的个数，要求摞法的方案数实际上是求从坐标（0，0）到坐标（5，5）的所有满足条件的路径数。

引例2、（进出栈问题）

思考过程：

本质上和姐妹洗碗问题一致，都是求方案数，且前提条件都是同种前提条件，即出栈的个数不能超过栈中存在的数的个数。

引例3、（找零问题）

思考过程：

本质上和姐妹洗碗问题一致，都是求方案数，且前提条件都是同种前提条件，即当前持有10元纸币排队的人数不能超过当前持有5元纸币排队的人数。

卡特兰序列通式分析

分析3的初始条件为f(0)=1,f(1)=1.

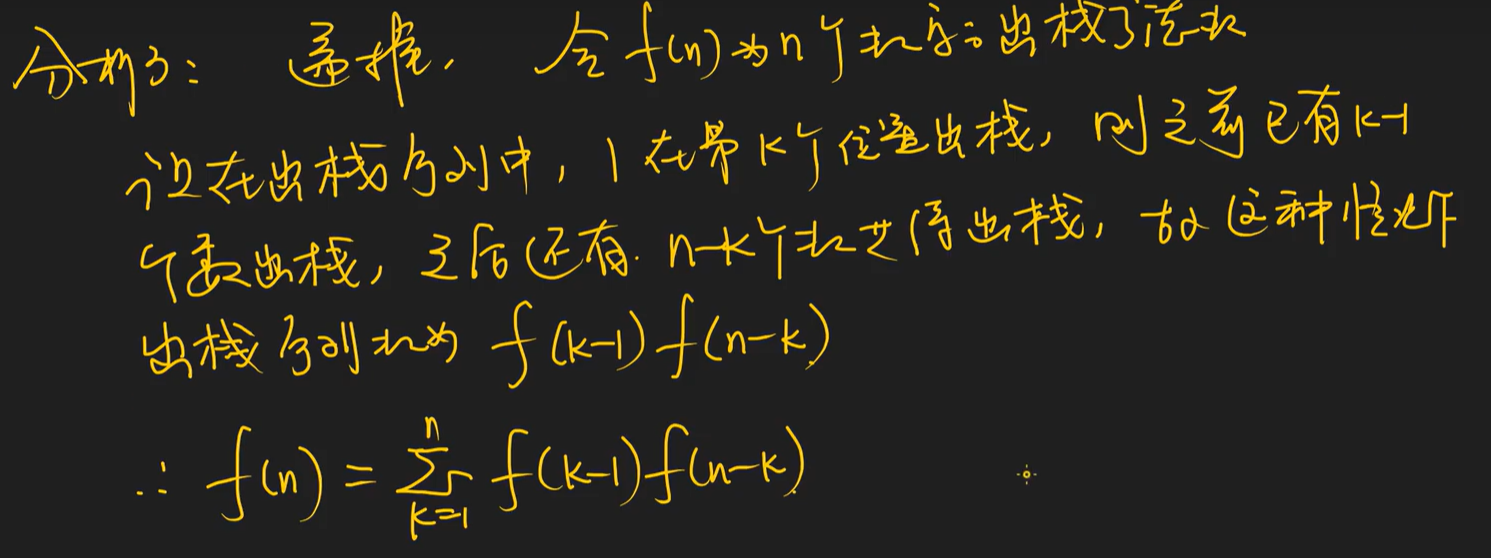
例题1：

例题2：

思路：将左括号看成1，右括号看成-1，由于左右括号要匹配，即数量要求相同，且当前右括号数量不能超过当前已经放好的左括号数量，故满足卡特兰数，即求上述方案数只需要算长度为n+1个数需要添加的括号数对n，则方案数为卡特兰数第n项。

例题3：

求解n个非叶子结点的二叉树总共有多少种？

思路：将每个非叶子结点看成它的左右结点的结合，而n个非叶子结点的二叉树的总数即为根节点的所有结合方案数，即为例题2中括号的放置方案，即卡特兰数的第n项。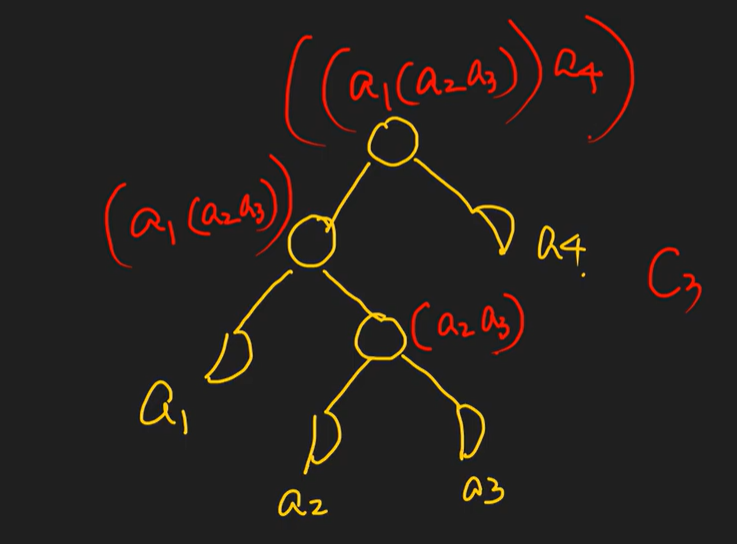

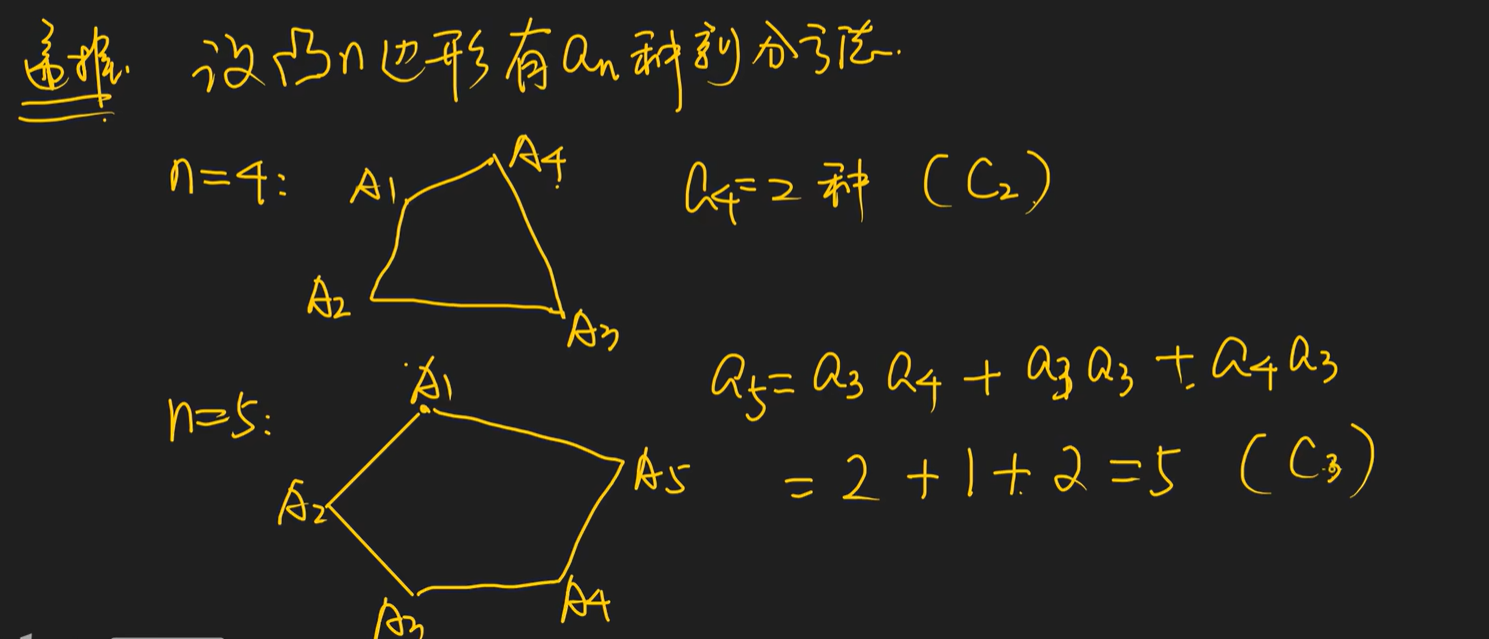
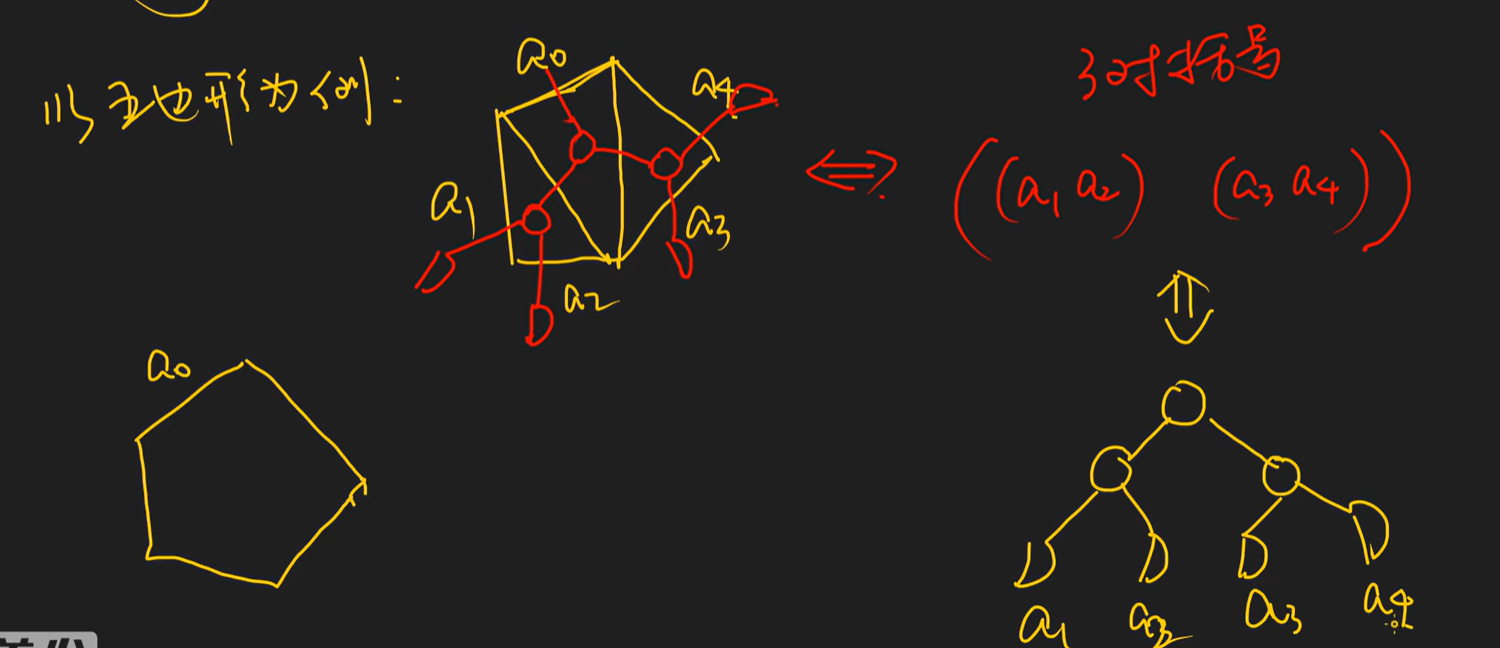
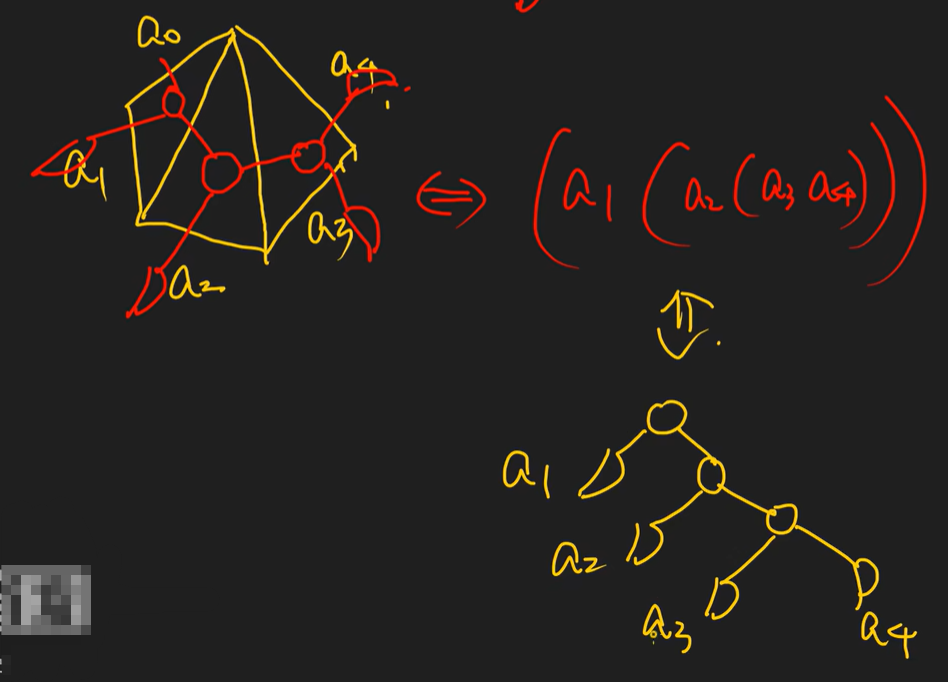
例题4：

思路：将该题转换为例题3二叉树，以a0边所在的区域作为根节点，每经过一条边，形成一个叶子结点或非叶子结点，如果线超出凸多边形，则形成的是叶子结点，否则形成的是非叶子结点，实际上只需要求出凸多边形的非叶子结点数n，则答案即为卡特兰数的第n项。

1.递推法：

2.分析法：

3.公式法：

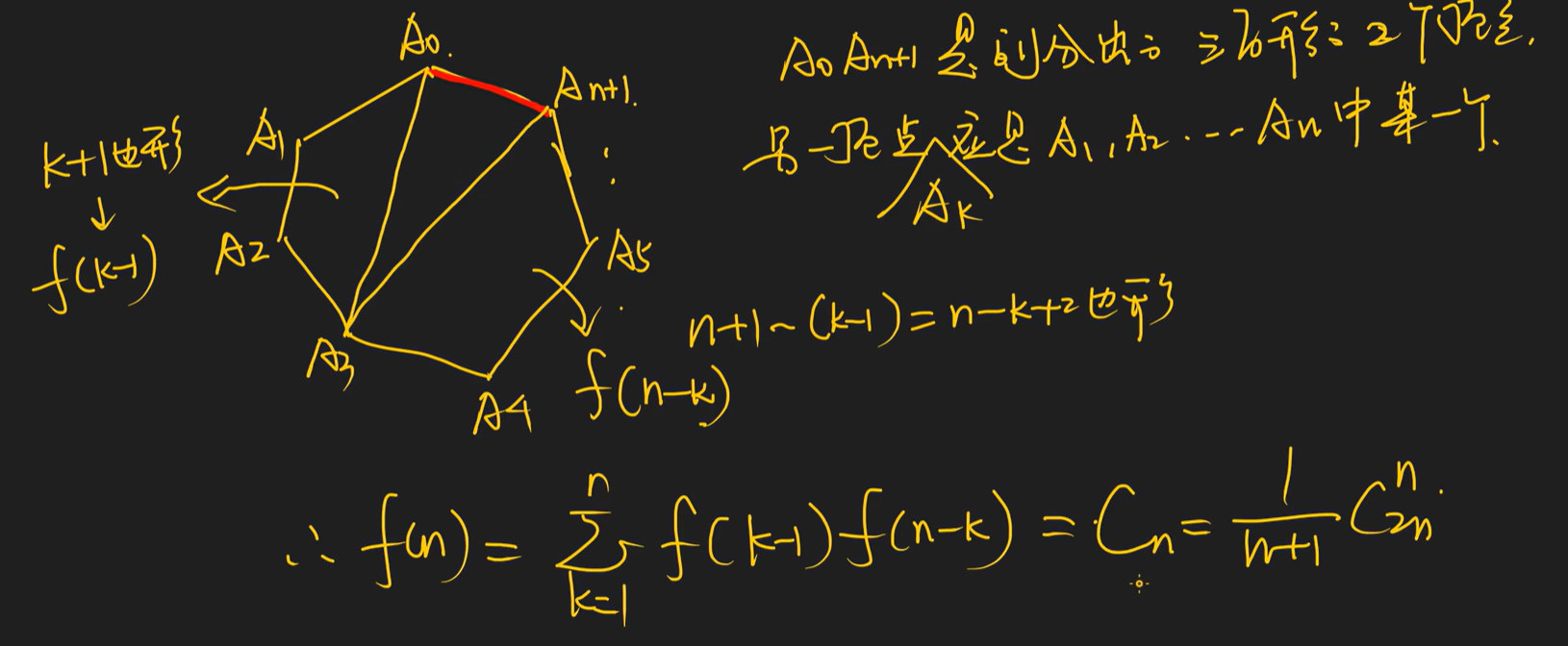
例题5：