洛谷P3374 【模板】树状数组 1-(单点修改,区间查询)

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 $x$

• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 $x$ 个数加上 $k$

• 2 x y 含义：输出区间 $[x,y]$ 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

输入输出样例

输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出 #1

14
16

说明/提示

【数据范围】

对于 30% 的数据，$1\le n\le 8$，$1\le m\le 10$；
对于 70% 的数据，$1\le n,m\le 1e4$；
对于 100%的数据，1≤n,m≤5e5。

数据保证对于任意时刻，$a$ 的任意子区间（包括长度为 $1$ 和 $n$ 的子区间）和均在 [−2^31,2^31) 范围内。

样例说明：

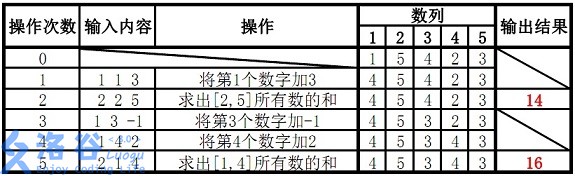
故输出结果14、16

代码实现：

树状数组实现：

#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
const int N=5e5+5;
int a[N],tr[N];
int n,m;
int lowbit(int x){
    return x&-x;
}
void add(int x,int y){
    for(int i=x;i<=n;i+=lowbit(i))tr[i]+=y;
}
int query(int x,int y){
    int res=0;
    for(int i=y;i;i-=lowbit(i))res+=tr[i];
    for(int i=x-1;i;i-=lowbit(i))res-=tr[i];
    return res;
}
signed main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
    	cin>>a[i];
    	add(i,a[i]);
	}
    while(m--){
        int x,y,z;
        cin>>x;
        if(x==1){
            cin>>y>>z;
            add(y,z);
        }else{
            cin>>y>>z;
            cout<<query(y,z)<<endl;
        }
    }
    return 0;
}

线段树实现：

#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
const int N=5e5+5;
int n,m;
int a[N];
struct node{
	int l,r,sum;
}tr[N*4];
void pushup(int u){
	tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
void build(int u,int l,int r){
	tr[u]={l,r};
	if(l==r){
		tr[u].sum=a[l];
		return;
	}
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
	pushup(u);
}
void modify(int u,int x,int z){
	if(tr[u].l==x&&tr[u].r==x)tr[u].sum+=z;
	else{
		int mid=tr[u].l+tr[u].r>>1;
		if(x<=mid)modify(u<<1,x,z);
		else modify(u<<1|1,x,z);
		pushup(u);
	}
}
int query(int u,int l,int r){
	if(tr[u].l>=l&&tr[u].r<=r)return tr[u].sum;
	int mid=tr[u].l+tr[u].r>>1;
	int res=0;
	if(r<=mid)res=query(u<<1,l,r);
	else if(l>mid)res=query(u<<1|1,l,r);
	else res=query(u<<1,l,mid)+query(u<<1|1,l,r);
	return res;
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	build(1,1,n);
	while(m--){
		int a,b,c;
		cin>>a>>b>>c;
		if(a==1)modify(1,b,c);
		else cout<<query(1,b,c)<<endl;
	}
	return 0;
}