7-5 有理数加法 (15 分)

1.题目描述：

本题要求编写程序，计算两个有理数的和。

输入格式：

输入在一行中按照a1/b1 a2/b2的格式给出两个分数形式的有理数，其中分子和分母全是整形范围内的正整数。

输出格式：

在一行中按照a/b的格式输出两个有理数的和。注意必须是该有理数的最简分数形式，若分母为1，则只输出分子。

输入样例1：

1/3 1/6

结尾无空行

输出样例1：

1/2

结尾无空行

输入样例2：

4/3 2/3

输出样例2：

2

 2.代码展示：

#include<bits/stdc++.h>
using namespace std;
//欧几里得算法 
int gcd(int a,int b)  //计算最大公约数
{
    if(b==0)return a;
    return gcd(b,a%b); 
}
int main()
{
    int a1,b1,a2,b2,fenzi,fenmu,d;
    scanf("%d/%d %d/%d",&a1,&b1,&a2,&b2);
    fenmu = b1 * b2;//计算两分数通分后的分母 
    fenzi = a1 * b2 + a2 * b1;//计算两分数通分后的分子和 
    d = gcd(fenzi,fenmu); //计算最大公约数
    //将分子和分母进行通分 
    fenzi /= d;
    fenmu /= d;
    //如果分母为1，则直接输出分子 
    if(fenmu == 1) printf("%d",fenzi);
    //否则按题目格式输出 
    else printf("%d/%d",fenzi,fenmu);
    return 0;
}

3.效果展示：

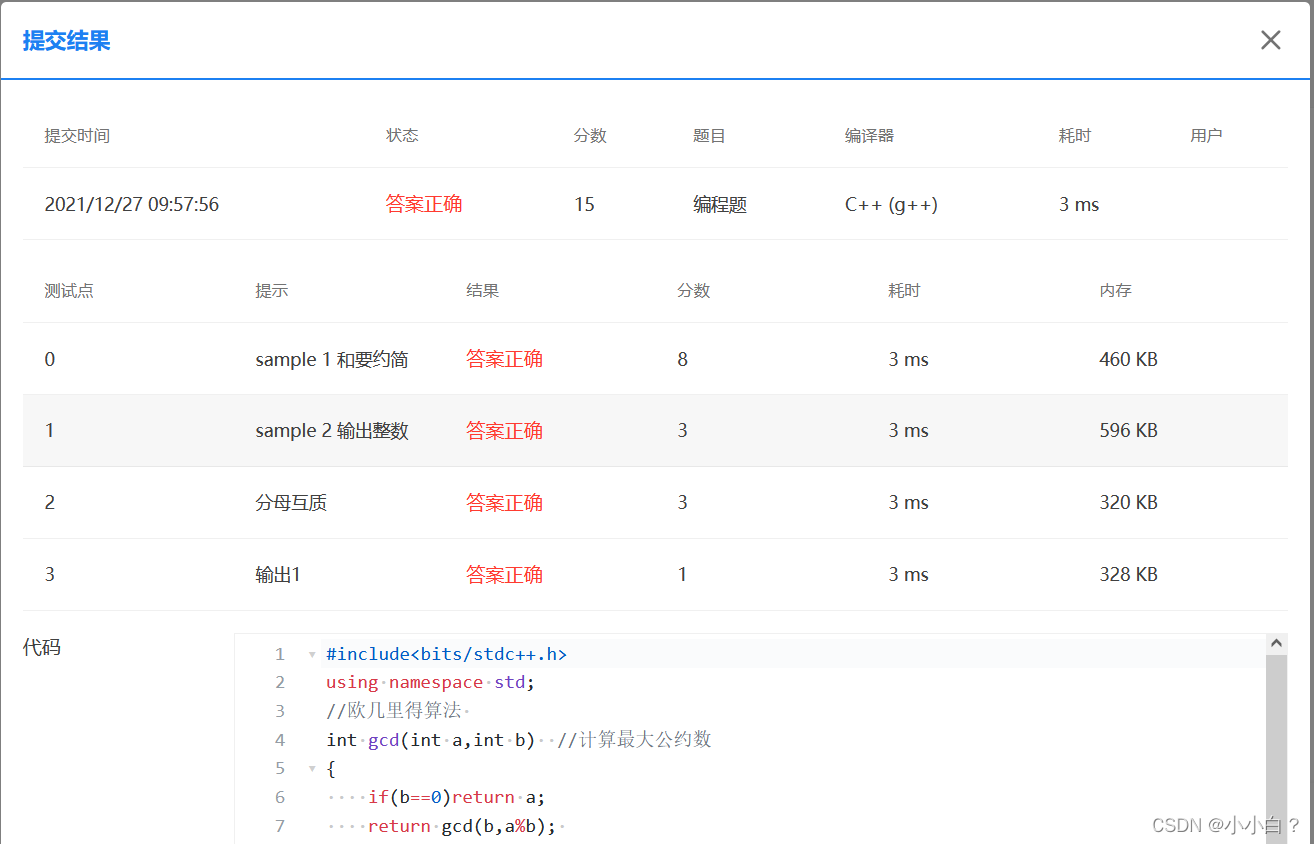
有需要的可以点击下方链接进行代码测试。

原题链接： https://pintia.cn/problem-sets/14/problems/813