manacher

manacher

\(manacher\)，一个可以做到 \(O(n)\) 求解一个字符串中的所有回文子串。

我们有一种 \(O(n^2)\) 的算法来求回文子串，枚举回文中心一点一点比较。

基于 \(O(n^2)\) 算法我们又有了一种 \(O(nlogn)\) 的算法，前后跑一遍 \(hash\)，再枚举回文中心，用 \(hash\) 比较，就可以做到 \(O(nlogn)\)

我们当然不能止步于此(毕竟大多数字符串算法都有 \(O(n)\) 算法)，就诞生了 \(manacher\)。

\(manacher\) 的基本思想是利用前面已匹配的的部分去更新后面的部分，我们用 \(d_i\) 来表示以 \(i\) 位置为回文中心的最大回文半径。我们当然不能直接判断，要用到两个东东来辅助我们判断，那就是当前找到的回文串的最右点，以及它的回文中心。

举个例子，如下图，当我们当前所在的位置为 \(i\) ，且 \(i\le r\) 时，我们知道可以找到 \(i\) 关于 \(mid\) 的对称点，由中点坐标公式可知，\(i\) 的对称点 \(j\) 满足 \(\frac{i+j}{2}=mid\)，也就是说， \(j\) 为 \(2\times mid -i\)，我们就可以直接用 \(j\) 的回文半径来更新 \(i\) 的了；当然，如果 \(j\) 的回文半径过于大，使得 \(i+d_j-1 > r\)，因为其实 \(r\) 之后的部分我们不能确定 \(i\) 与 \(j\) 的一致，那么我们的转移即为

\[ d_i=min(d_j,r-i+1) (i\le r) \]

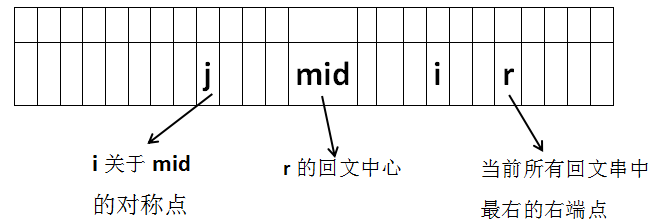
还有一种情况，如下图，我们的 \(i\) 大于我们的 \(r\)，那么我们知道我们无法用之前的信息去更新 \(d_i\)，那么我们就暴力更新。

我们最终就可以找到所有的奇回文串了。

那么我们怎样找到所有的偶回文串呢？

其实很简单，我们可以将字符与字符之间加上一个没有出现在字符串中的字符，如 \(\#,\%,*\) 等，再在前后加一个不一样且互不相同的字符，比如在前面加 ~,并在后面加个 \(*\)(这样做是为了防止数组越界)，这样我们就可以同时求出奇回文串和偶回文串了。

由于 \(r\) 单调递增，与 \(i\) 搭配类似于双指针，所以我们的复杂度就为 \(O(n)\) 了。

\(code\)

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=3e7;
char ch[N/2];
char S[N];
int R[N];
void manacher(char *s){
    int len=strlen(s+1);
    int cnt=0;
    S[0]='~',S[++cnt]='#';
    for(int i=1;i<=len;i++)S[++cnt]=s[i],S[++cnt]='#';
    S[++cnt]='*';
    int r=0,mid=0;
    int ans=0;
    for(int i=1;i<=cnt;i++){
        if(i<=r)R[i]=min(R[(mid<<1)-i],r-i+1);
        else R[i]=1;
        while(S[i+R[i]]==S[i-R[i]])R[i]++;
        if(i+R[i]-1>r)r=i+R[i]-1,mid=i;
        ans=max(ans,R[i]);
    }
    printf("%d\n",ans-1);
}
int main(){
    scanf("%s",ch+1);
    manacher(ch);
    return 0;
}