算法入门：递归和迭代

文章目录

1.递归 

• 1.1.概念
• 1.2.案例
• 1.3.优缺点

2.迭代

• 2.1.概念
• 2.2.案例
• 2.3.优缺点

3.递归与迭代算法的关系和区别

• 3.1.关系
• 3.2.区别
• 3.3.算法的选择

 

1.递归

1.1.概念

递归算法是一种解决问题的方法，其中问题被分解为更小、相似的子问题。这一方法通过不断调用自身来解决这些子问题，直到达到基本情况为止。递归算法包括两个关键要素：递归定义和基本情况。

1. 递归定义：描述如何将原始问题分解为更小的同类问题。递归函数会反复调用自身，每次处理一个子问题。

2. 基本情况：定义递归过程何时结束的条件。一旦达到基本情况，递归停止，开始回溯并组合子问题的解以得到原始问题的解。

递归算法的优势在于能够通过简单而优雅的方式解决复杂问题，但需要确保递归调用朝着基本情况逼近，以避免无限递归。在实际应用中，递归算法有助于提高代码的可读性和简洁性。

注意：递归必须要有一个退出的条件!

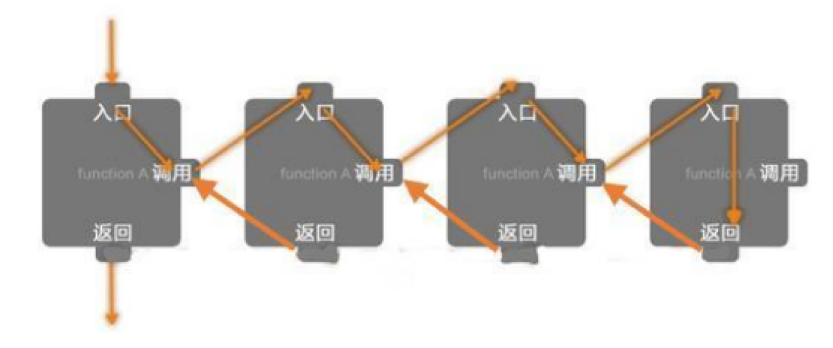
递归算法解决问题的特点：

1. 自调用特性：递归是一种通过在算法或函数内部调用自身的方法。这使得问题被分解为更小的、相似的子问题，从而实现问题的逐层解决。

2. 递归出口：递归策略必须定义一个明确的递归结束条件，通常称为递归出口或基本情况。这是确保递归不会无限进行的关键。

3. 简洁性与效率权衡：递归算法通常以简洁的形式表达问题解决方式，但其运行效率相对较低。因此，尽管递归提供了清晰的问题描述，但在实际程序设计中，不一定总是首选，特别是对于涉及大量重复计算的问题。

4. 栈空间开销：在递归调用过程中，系统为每一层递归开辟栈空间以存储返回点、局部变量等信息。递归次数过多可能导致栈溢出等问题，因此在设计程序时需要注意栈空间的管理。

在构建递归算法时，确保定义一个明确的递归出口是至关重要的。递归出口是指一个条件，当满足该条件时，递归过程将终止，不再进行进一步的自我调用。这一条件的设定对于有效控制递归的深度和确保算法终止是必不可少的。在递归算法设计中，正确而清晰地定义递归出口是保证算法正确性和避免无限递归的关键因素。

 

1.2.案例

• 1.阶乘计算： 通过递归方式计算 n 的阶乘，即 n!。阶乘 n! = n * (n-1) * (n-2) * …* 1(n>0)

using System;

class Program
{
    static void Main()
    {
        Console.WriteLine("请输入要计算阶乘的数字：");
        
        // 从用户输入获取要计算阶乘的数字
        int n = Convert.ToInt32(Console.ReadLine());

        // 调用阶乘函数并输出结果
        long result = Factorial(n);
        Console.WriteLine($"{n} 的阶乘是：{result}");
    }

    // 阶乘计算函数，使用递归实现
    static long Factorial(int num)
    {
        // 递归出口：当 num 为 0 或 1 时，阶乘为 1
        if (num == 0 || num == 1)
        {
            return 1;
        }
        else
        {
            // 递归调用，将问题分解为更小的子问题
            // 例如：5! = 5 * 4!
            return num * Factorial(num - 1);
        }
    }
}

输入一个整数，然后通过递归算法计算该整数的阶乘，并输出结果。递归函数 Factorial 中包含了递归出口和递归调用，确保在递归过程中逐步减小问题的规模，最终达到递归出口。

 

• 2.斐波那契数列： 使用递归计算斐波那契数列的第 n 项。斐波纳契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……这个数列从第三项开始，每一项都等于前两项之和。

using System;

class Program
{
    static void Main()
    {
        Console.WriteLine("请输入斐波那契数列的项数：");

        // 从用户输入获取斐波那契数列的项数
        int n = Convert.ToInt32(Console.ReadLine());

        // 输出斐波那契数列的前 n 项
        Console.WriteLine($"斐波那契数列的前 {n} 项为：");
        for (int i = 0; i < n; i++)
        {
            Console.Write(Fibonacci(i) + " ");
        }
    }

    // 斐波那契数列计算函数，使用递归实现
    static int Fibonacci(int num)
    {
        // 递归出口：当 num 为 0 或 1 时，斐波那契数为 num
        if (num == 0 || num == 1)
        {
            return num;
        }
        else
        {
            // 递归调用，将问题分解为两个子问题
            // 例如：Fibonacci(5) = Fibonacci(4) + Fibonacci(3)
            return Fibonacci(num - 1) + Fibonacci(num - 2);
        }
    }
}

输入斐波那契数列的项数，通过递归算法计算并输出斐波那契数列的前 n 项。递归函数 Fibonacci 中包含了递归出口和递归调用，确保在递归过程中逐步减小问题的规模，最终达到递归出口。需要注意，递归实现在计算较大的斐波那契数列项时可能效率较低，存在重复计算的情况。

 

• 3.二叉树遍历： 通过递归方式实现二叉树的前序、中序、后序遍历。

using System;

// 定义二叉树节点类
class TreeNode
{
    public int Value { get; set; }
    public TreeNode Left { get; set; }
    public TreeNode Right { get; set; }

    public TreeNode(int value)
    {
        Value = value;
        Left = null;
        Right = null;
    }
}

class BinaryTreeTraversal
{
    static void Main()
    {
        // 构建一个简单的二叉树
        TreeNode root = new TreeNode(1);
        root.Left = new TreeNode(2);
        root.Right = new TreeNode(3);
        root.Left.Left = new TreeNode(4);
        root.Left.Right = new TreeNode(5);

        Console.WriteLine("前序遍历结果：");
        PreorderTraversal(root);

        Console.WriteLine("\n中序遍历结果：");
        InorderTraversal(root);

        Console.WriteLine("\n后序遍历结果：");
        PostorderTraversal(root);
    }

    // 二叉树前序遍历
    static void PreorderTraversal(TreeNode node)
    {
        if (node != null)
        {
            // 访问当前节点
            Console.Write(node.Value + " ");
            
            // 递归遍历左子树
            PreorderTraversal(node.Left);
            
            // 递归遍历右子树
            PreorderTraversal(node.Right);
        }
    }

    // 二叉树中序遍历
    static void InorderTraversal(TreeNode node)
    {
        if (node != null)
        {
            // 递归遍历左子树
            InorderTraversal(node.Left);

            // 访问当前节点
            Console.Write(node.Value + " ");
            
            // 递归遍历右子树
            InorderTraversal(node.Right);
        }
    }

    // 二叉树后序遍历
    static void PostorderTraversal(TreeNode node)
    {
        if (node != null)
        {
            // 递归遍历左子树
            PostorderTraversal(node.Left);
            
            // 递归遍历右子树
            PostorderTraversal(node.Right);

            // 访问当前节点
            Console.Write(node.Value + " ");
        }
    }
}

示例中，定义了一个简单的二叉树节点类 TreeNode，并使用递归算法实现了二叉树的前序、中序和后序遍历。这三种遍历方式分别按照根节点的访问顺序。

 

• 4.汉诺塔问题： 经典的递归问题，将一堆盘子从一个柱子移动到另一个柱子，保持规定的顺序。

汉诺塔问题是一个经典的数学问题，起源于印度。问题的设定是有三个柱子（通常称为A、B、C）和一些盘子，盘子的大小各不相同，它们以递减的顺序从大到小依次叠放在柱子A上。目标是将所有的盘子从柱子A移动到柱子C，借助柱子B作为辅助。

汉诺塔问题的规则如下：

1. 只能每次移动一个盘子。
2. 每次移动时，只能从某个柱子的顶端取走一个盘子放在另一个柱子的顶端。
3. 移动过程中，大盘子不能放在小盘子上面。

问题的关键在于如何将整个问题分解为子问题，并通过递归的方式逐步解决。经典的递归算法如下：

1. 将 n-1 个盘子从柱子A移动到柱子B，借助柱子C作为辅助。
2. 将第 n 个盘子从柱子A移动到柱子C。
3. 将 n-1 个盘子从柱子B移动到柱子C，借助柱子A作为辅助。

这样，问题就被成功地分解为规模较小的子问题。递归调用这个过程，直到盘子数量为1时，直接移动到目标柱子即可。递归的出口是只有一个盘子的情况。整个过程的实现通过递归算法使得步骤清晰而简洁。

using System;

class Program
{
    static void Main()
    {
        Console.WriteLine("请输入盘子的数量：");

        // 从用户输入获取盘子的数量
        int n = Convert.ToInt32(Console.ReadLine());

        Console.WriteLine($"移动 {n} 个盘子的步骤如下：");
        Hanoi(n, 'A', 'B', 'C');
    }

    // 汉诺塔问题的递归解法
    // 参数说明：
    // n: 盘子的数量
    // source: 源柱子
    // auxiliary: 辅助柱子
    // target: 目标柱子
    static void Hanoi(int n, char source, char auxiliary, char target)
    {
        // 递归出口：当只有一个盘子时直接从源柱子移动到目标柱子
        if (n == 1)
        {
            Console.WriteLine($"移动盘子 {n} 从 {source} 到 {target}");
        }
        else
        {
            // 递归调用，将 n-1 个盘子从源柱子移动到辅助柱子
            Hanoi(n - 1, source, target, auxiliary);

            // 移动第 n 个盘子从源柱子到目标柱子
            Console.WriteLine($"移动盘子 {n} 从 {source} 到 {target}");

            // 递归调用，将 n-1 个盘子从辅助柱子移动到目标柱子
            Hanoi(n - 1, auxiliary, source, target);
        }
    }
}

通过递归算法实现了汉诺塔问题的移动步骤。递归函数 Hanoi 中包含了递归出口和递归调用，确保在递归过程中逐步减小问题的规模，最终达到递归出口。

 

• 5.包含前面排序算法中的快速排序算法案例。

 

1.3.优缺点

优点：

1.清晰简洁： 递归算法通常能够以更简洁的方式表达问题解决方式，具有直观性。

2.自然表示分治： 递归天然适合分治思想，能够将问题自然分解为子问题，使得代码结构清晰。

缺点：

1.性能开销： 递归调用会产生额外的函数调用开销和栈空间占用，可能导致性能较低。

2.栈溢出： 递归层次过多可能导致栈溢出，尤其在处理大规模数据时容易发生。

3.难以理解和调试： 对于一些复杂的递归算法，可能会难以理解和调试。

 

 

2.迭代

2.1.概念

迭代算法是一种通过反复执行一组指令来解决问题的方法。与递归算法不同，迭代算法不涉及自我调用，而是通过循环结构反复执行一定的步骤，直至达到问题的解决或终止条件。

迭代算法的特点包括：

1. 循环结构：使用循环结构反复执行一组指令，每次迭代都向问题解决迈进一步。

2. 明确终止条件：迭代算法必须定义明确的终止条件，以确保循环不会无限进行。这一条件标志着算法已经完成任务或达到了所需的解。

3. 无递归调用：与递归算法不同，迭代算法不涉及函数或方法的自我调用。算法通过重复执行相同的操作来逐步逼近问题的解。

4. 效率：迭代算法通常具有较高的运行效率，尤其在处理大规模数据或需要重复执行相似操作的情况下。

迭代算法通过循环结构、明确的终止条件和无递归调用的方式提供了一种直观而高效的问题解决方法。

特点：

迭代法，又被称为辗转法，是一种通过反复使用变量的先前值来递推新值的过程。与迭代法相对应的是直接法，也称为一次解法，其特点是一次性解决问题。

在迭代法中，问题的解决通过多次迭代步骤逐渐逼近，每一步都利用先前的值计算出新的值。这反映了迭代法的渐进逼近性质，使得问题的解随着迭代的进行逐步精炼。

与直接法不同，迭代法通过多次迭代过程，通过递推更新变量的值，逐步逼近问题的最终解。这种方法常用于处理复杂问题，其中直接求解可能困难或不可行。

 

2.2.案例

• 1.阶乘计算： 通过循环迭代方式计算 n 的阶乘。

using System;

class Program
{
    static void Main()
    {
        Console.WriteLine("请输入要计算阶乘的数字：");

        // 从用户输入获取要计算阶乘的数字
        int n = Convert.ToInt32(Console.ReadLine());

        // 调用阶乘函数并输出结果
        long result = Factorial(n);
        Console.WriteLine($"{n} 的阶乘是：{result}");
    }

    // 阶乘计算函数，使用迭代实现
    static long Factorial(int num)
    {
        // 初始结果设为1
        long result = 1;

        // 迭代计算阶乘，从1到num逐步相乘
        for (int i = 1; i <= num; i++)
        {
            result *= i;
        }

        return result;
    }
}

迭代函数 Factorial 中使用了循环结构，从1到输入的整数逐步相乘，得到阶乘的结果。这种迭代方式避免了递归中可能发生的栈溢出问题，并在计算阶乘时具有较高的效率。

 

• 2.斐波那契数列： 使用循环迭代计算斐波那契数列的第 n 项。

using System;

class Program
{
    static void Main()
    {
        Console.WriteLine("请输入斐波那契数列的项数：");

        // 从用户输入获取斐波那契数列的项数
        int n = Convert.ToInt32(Console.ReadLine());

        // 输出斐波那契数列的前 n 项
        Console.WriteLine($"斐波那契数列的前 {n} 项为：");
        for (int i = 0; i < n; i++)
        {
            Console.Write(Fibonacci(i) + " ");
        }
    }

    // 斐波那契数列计算函数，使用迭代实现
    static int Fibonacci(int num)
    {
        // 前两项分别为0和1
        if (num == 0) return 0;
        if (num == 1) return 1;

        // 初始的前两项值
        int fib0 = 0;
        int fib1 = 1;
        int fibResult = 0;

        // 从第三项开始迭代计算
        for (int i = 2; i <= num; i++)
        {
            // 当前项等于前两项之和
            fibResult = fib0 + fib1;

            // 更新前两项的值
            fib0 = fib1;
            fib1 = fibResult;
        }

        return fibResult;
    }
}

通过迭代算法计算并输出斐波那契数列的前 n 项。迭代函数 Fibonacci 中使用了循环结构，从第三项开始逐步计算斐波那契数列的值。

 

• 3.二叉树遍历： 通过循环迭代方式实现二叉树的前序、中序、后序遍历。

using System;
using System.Collections.Generic;

// 定义二叉树节点类
class TreeNode
{
    public int Value { get; set; }
    public TreeNode Left { get; set; }
    public TreeNode Right { get; set; }

    public TreeNode(int value)
    {
        Value = value;
        Left = null;
        Right = null;
    }
}

class BinaryTreeTraversal
{
    static void Main()
    {
        // 构建一个简单的二叉树
        TreeNode root = new TreeNode(1);
        root.Left = new TreeNode(2);
        root.Right = new TreeNode(3);
        root.Left.Left = new TreeNode(4);
        root.Left.Right = new TreeNode(5);

        Console.WriteLine("前序遍历结果：");
        PreorderTraversal(root);

        Console.WriteLine("\n中序遍历结果：");
        InorderTraversal(root);

        Console.WriteLine("\n后序遍历结果：");
        PostorderTraversal(root);
    }

    // 二叉树前序遍历，迭代实现
    static void PreorderTraversal(TreeNode root)
    {
        if (root == null)
            return;

        // 使用栈来辅助迭代
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.Push(root);

        while (stack.Count > 0)
        {
            TreeNode node = stack.Pop();
            Console.Write(node.Value + " ");

            // 先将右子树入栈，再将左子树入栈
            if (node.Right != null)
                stack.Push(node.Right);
            if (node.Left != null)
                stack.Push(node.Left);
        }
    }

    // 二叉树中序遍历，迭代实现
    static void InorderTraversal(TreeNode root)
    {
        if (root == null)
            return;

        // 使用栈来辅助迭代
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode current = root;

        while (current != null || stack.Count > 0)
        {
            // 将左子树入栈
            while (current != null)
            {
                stack.Push(current);
                current = current.Left;
            }

            // 出栈并访问节点，然后转向右子树
            current = stack.Pop();
            Console.Write(current.Value + " ");
            current = current.Right;
        }
    }

    // 二叉树后序遍历，迭代实现
    static void PostorderTraversal(TreeNode root)
    {
        if (root == null)
            return;

        // 使用两个栈来辅助迭代
        Stack<TreeNode> stack1 = new Stack<TreeNode>();
        Stack<TreeNode> stack2 = new Stack<TreeNode>();

        stack1.Push(root);

        while (stack1.Count > 0)
        {
            TreeNode node = stack1.Pop();
            stack2.Push(node);

            // 先将左子树入栈，再将右子树入栈
            if (node.Left != null)
                stack1.Push(node.Left);
            if (node.Right != null)
                stack1.Push(node.Right);
        }

        // 出栈并访问节点
        while (stack2.Count > 0)
        {
            Console.Write(stack2.Pop().Value + " ");
        }
    }
}

使用迭代算法实现了二叉树的前序、中序和后序遍历。使用栈来辅助迭代，通过迭代的方式模拟递归遍历的过程，实现了二叉树的各种遍历方式。

 

2.3.优缺点

优点：

1.性能高效： 通常迭代算法在性能上比递归更高效，因为它避免了函数调用的开销和栈空间的使用。

2.避免栈溢出： 迭代方式不会导致栈溢出问题，可以处理大规模数据。

3.易于优化： 一些编译器和解释器能够对迭代算法进行更好的优化，提高执行效率。

缺点：

1.代码可能冗长： 有些问题的迭代实现可能相对冗长，因为需要手动管理循环和状态。

2.不如递归直观： 对于一些递归天然表达的问题，迭代实现可能不如递归直观。

 

3.递归与迭代算法的关系和区别

3.1.关系

1. 问题解决方式：递归算法和迭代算法都是用于解决问题的方法，只是它们采取了不同的策略。

2. 问题分解：者都可以通过将问题分解为更小的子问题来逐步解决原始问题。

 

3.2.区别

1. 调用方式：

• 递归算法：自身调用的方式，函数或方法在解决问题时会反复调用自身。
• 迭代算法：通过循环结构进行多次迭代，不涉及自我调用。

2. 实现方式：

• 递归算法：通常更简洁清晰，能够以较短的代码表达问题解决方式。
• 迭代算法：可能需要更多的代码，但通常在一些情况下具有更高的运行效率。

3. 性能：

• 递归算法：可能由于递归调用导致栈溢出，效率相对较低。
• 迭代算法：通常具有较高的运行效率，尤其在循环次数较多的情况下。

4. 终止条件：

• 递归算法：必须有一个明确的递归结束条件，否则可能导致无限递归。
• 迭代算法：通过循环结构和终止条件来确保算法的终止。

在实际应用中，选择使用递归还是迭代通常取决于问题的性质、可读性、代码复杂度以及性能要求等因素。有些问题更适合通过递归解决，而另一些问题则可能更适合迭代。

 

3.3.算法的选择

1. 递归的选择：

• 当问题可以自然地分解为子问题时，递归通常更为合适，代码更简洁。
• 对于树形结构的问题（如二叉树遍历），递归能够更自然地反映问题的结构。

2. 迭代的选择：

• 当性能要求较高，或者递归层次较深可能导致栈溢出时，迭代是更好的选择。
• 一些问题的迭代实现可能更容易理解和调试，特别是在处理循环结构的问题时。

对于阶乘计算、斐波那契数列、二叉树遍历等问题，递归算法可以提供清晰简洁的解决方式，但在实际应用中需要注意性能和可能的栈溢出问题。迭代算法在性能和空间利用上通常更为高效，适用于需要迭代处理的问题。在选择算法时，需要权衡这些因素，根据具体问题和需求做出合适的选择。