引言
贝叶斯网络是机器学习中非常经典的算法之一,它能够根据已知的条件来估算出不确定的知识,应用范围非常的广泛。贝叶斯网络以贝叶斯公式为理论接触构建成了一个有向无环图,我们可以通过贝叶斯网络构建的图清晰的根据已有信息预测未来信息。贝叶斯网络适用于表达和分析不确定性和概率性的事件,应用于有条件地依赖多种控制因素的决策,可以从不完全、不精确或不确定的知识或信息中做出推理。本文从朴素贝叶斯模型开始,详细描述了贝叶斯网络的意义,构建方案以及其他衍生算法。
预备知识
最大熵模型、概率统计
一、朴素贝叶斯
1、朴素贝叶斯假设(与贝叶斯网络区别)
一个特征出现的概率,与其他特征(条件)独立(特征独立性),其实是:对于给定分类的条件下,特征独立
每个特征同等重要(特征均衡性)
例子:文本分类问题:
样本:10000封邮件,每个邮件被标记为垃圾邮件或者非垃圾邮件
分类目标:给定第10001封邮件,确定它是垃圾邮件还是非垃圾邮件
方法:朴素贝叶斯
类别c:垃圾邮件c1,非垃圾邮件c2
词汇表,两种建立方法:
1、使用现成的单词词典;2、将所有邮件中出现的单词都统计出来,得到词典。
记单词数目为N
将每个邮件m映射成维度为N的向量xn
若单词wi在邮件m中出现过,则xi=1,否则,xi=0。即邮件的向量化:m-->(x1,x2……xN)o
贝叶斯公式:P(c|x)=P(x|c)*P(c)/P(x)
P(c1|x)=P(x|c1)*P(c1)/P(x)
P(c2|x)=P(x|c2)*P(c2)/P(x)
注意这里x是向量
P(c|x)=P(x|c)*P(c)/P(x)
P(x|c)=P(x1,x2…xN|c)=P(x1|c)*P(x2|c)…P(xN|c)
特征条件独立假设
P(x)=P(x1,x2…xN)=P(x1)*P(x2)…P(xN)
特征独立假设
带入公式:P(c|x)=P(x|c)*P(c)/P(x)
o等式右侧各项的含义:
nP(xi|cj):在cj(此题目,cj要么为垃圾邮件1,要么为非垃圾邮件2)的前提下,第i个单词xi出现的概率
nP(xi):在所有样本中,单词xi出现的概率
nP(cj):在所有样本中,邮件类别cj出现的概率
拉普拉斯平滑(防止是0的情况)
p(x1|c1)是指的:在垃圾邮件c1这个类别中,单词x1出现的概率。(x1是待考察的邮件中的某个单词)
定义符号:
n1:在所有垃圾邮件中单词x1出现的次数。如果x1没有出现过,则n1=0。
nn:属于c1类的所有文档的出现过的单词总数目。
o得到公式:
o拉普拉斯平滑:
n其中,N是所有单词的数目。修正分母是为了保证概率和为1
同理,以同样的平滑方案处理p(x1)
二、贝叶斯网络
把某个研究系统中涉及的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。
贝叶斯网络,又称有向无环图模型(DAG),是一种概率图模型,根据概率图的拓扑结构,考察一组随机变量{X1,X2...Xn}及其n组条件概率分布(CPD)的性质。
一般而言,贝叶斯网络的有向无环图中的节点表示随机变量,它们可以是可观察到的变量,或隐变量、未知参数等。连接两个节点的箭头代表此两个随机变量是具有因果关系(或非条件独立)。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(children)”,两节点就会产生一个条件概率值。
每个结点在给定其直接前驱时,条件独立于其非后继。
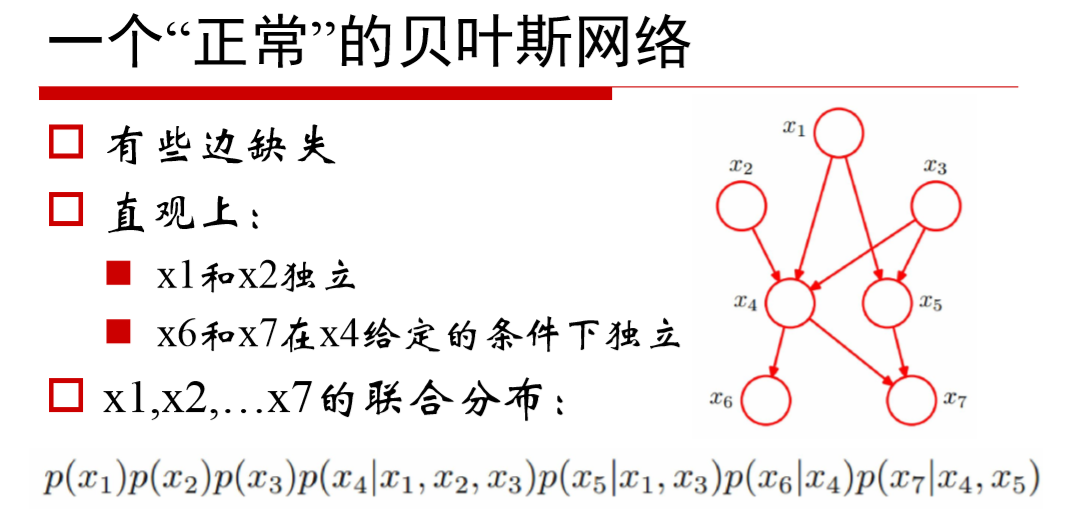
三、马尔科夫模型
贝叶斯网络简化形成一条链式模型,Ai+1只与Ai有关,与A1,…,Ai-1无关。
![]()
隐马尔科夫模型:

四、通过贝叶斯网络判断条件独立:

五、贝叶斯网络的构建
依次计算每个变量的D-separation的局部测试结果,综合每个结点得到贝叶斯网络。
算法过程:
选择变量的一个合理顺序:X1,X2,...Xn
对于i=1到n
o在网络中添加Xi结点
在X1,X2,...Xi-1中选择Xi的父母,使得:
![]()
o这种构造方法,显然保证了全局的语义要求:
![]()
问题,如果碰到了混合(离散+连续)的网络怎么办-->信号函数离散化




