codeforces 633D - Fibonacci-ish 离散化 + 二分查询

Fibonacci-ish

Yash has recently learnt about the Fibonacci sequence and is very excited about it. He calls a sequence Fibonacci-ish if

1. the sequence consists of at least two elements
2. f₀ and f₁ are arbitrary
3. f_n + 2 = f_n + 1 + f_n for all n ≥ 0.

You are given some sequence of integers a₁, a₂, ..., a_n. Your task is rearrange elements of this sequence in such a way that its longest possible prefix is Fibonacci-ish sequence.

Input

The first line of the input contains a single integer n (2 ≤ n ≤ 1000) — the length of the sequence a_i.

The second line contains n integers a₁, a₂, ..., a_n (|a_i| ≤ 10⁹).

Output

Print the length of the longest possible Fibonacci-ish prefix of the given sequence after rearrangement.

Examples

Input

3
1 2 -1

Output

3

Input

5
28 35 7 14 21

Output

4

Note

In the first sample, if we rearrange elements of the sequence as  - 1, 2, 1, the whole sequence a_i would be Fibonacci-ish.

In the second sample, the optimal way to rearrange elements is 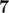, , , , 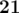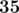28.

思路:由于斐波那契数列数值成指数型增长(称为斐波那契数列的收敛性)，所以实际可选的长度不会超过100(实际上增长速度比2的幂次方要慢，若是正整数的斐波那契数列，要从0 1增长到1e9只需40位左右，所以题解给出的长度最大也是接近90的)；那么只需离散出全部的不同的数值及其个数，枚举前两位即可；特例是前两位为0，这时长度可能达到1000，但只会出现一次；

实现细节:用stk记录下路径上的序号，为了方便每次枚举时，初始化每个数的个数；同时也可递推出当前两位的和；

没使用map,使用map的话，插入和查询都是log(n),总时间复杂度为O(n^2*log(n)*len)len为每次搜索的长度，且常数较大；用数组模拟，时间复杂度中少了log(n)与map带来的额外的常数，只需46ms 0k

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<vector>
#include<cmath>
#include<stdlib.h>
#include<time.h>
#include<stack>
#include<set>
#include<map>
#include<queue>
using namespace std;
#define rep0(i,l,r) for(int i = (l);i < (r);i++)
#define rep1(i,l,r) for(int i = (l);i <= (r);i++)
#define rep_0(i,r,l) for(int i = (r);i > (l);i--)
#define rep_1(i,r,l) for(int i = (r);i >= (l);i--)
#define MS0(a) memset(a,0,sizeof(a))
#define MS1(a) memset(a,-1,sizeof(a))
#define MSi(a) memset(a,0x3f,sizeof(a))
#define inf 0x3f3f3f3f
#define lson l, m, rt << 1
#define rson m+1, r, rt << 1|1
typedef __int64 ll;
template<typename T>
void read1(T &m)
{
    T x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    m = x*f;
}
template<typename T>
void read2(T &a,T &b){read1(a);read1(b);}
template<typename T>
void read3(T &a,T &b,T &c){read1(a);read1(b);read1(c);}
template<typename T>
void out(T a)
{
    if(a>9) out(a/10);
    putchar(a%10+'0');
}
int v[1010],num[1010],stk[1010];//stk长度也要为1000，因为前面两个为0时,len可能为最大值
int main()
{
    int n;
    read1(n);
    rep0(i,0,n) read1(v[i]);
    sort(v,v + n);
    int ans = 0,cnt = 0;
    rep0(i,0,n){
        int t = i;
        while(i < n - 1 && v[i] == v[i + 1]) i++;
        num[cnt] = i - t + 1;
        v[cnt++] = v[i];//压缩
    }
    v[cnt] = 2e9;
    rep0(i,0,cnt){
        rep0(j,0,cnt){
            if(i != j || num[j] > 1){
                stk[1] = i;stk[2] = j;
                int len = 2,val = v[i] + v[j];
                num[i]--,num[j]--;
                int down = lower_bound(v,v+cnt,val) - v;
                while(v[down] == val && num[down]){
                    num[down]--;
                    val -= v[stk[len-1]];
                    val += v[down];
                    stk[++len] = down;
                    down = lower_bound(v,v+cnt,val) - v;
                }
                ans = max(ans,len);
                rep1(i,1,len) num[stk[i]]++;
            }
        }
    }
    out(ans);
    return 0;
}