星座图的原理与应用
I、Q调制和星座图
一个信号有三个特性随时间变化:幅度、相位或频率。然而,相位和频率仅仅是从不同的角度去观察或测量同一信号的变化。人们可以同时进行幅度和相位的调制,也可以分开进行调制,但是这既难于产生更难于检测。但是在特制的系统中信号可以分解为一组相对独立的分量:同相(I)和正交(Q)分量。这两个分量是正交的,且互不相干的。
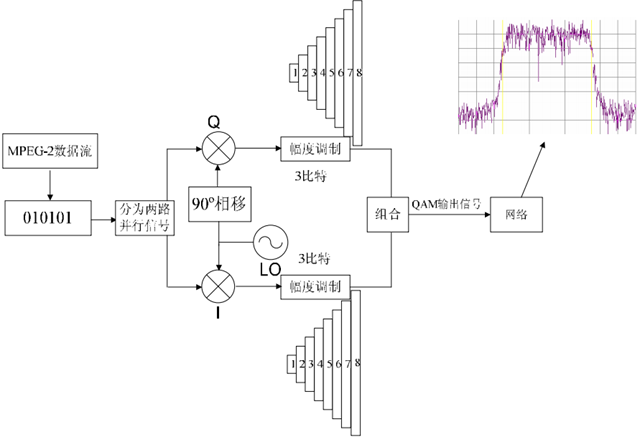
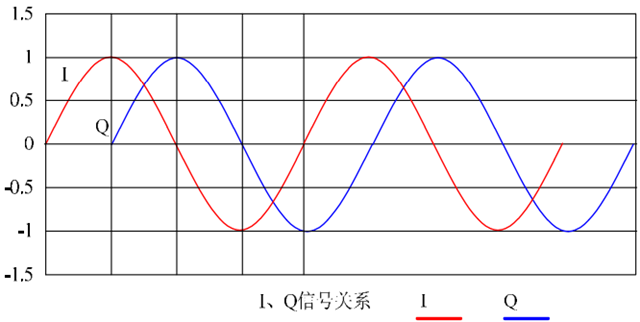
图1中的QAM调制器中I和Q信号来自一个信号源,幅度和频率都相同,唯一不同的是Q 信号的相位与I信号相差90度 。具体关系如图2所示,当I的幅度为1的时候,Q的幅度为0,而当I的幅度为0的时候,Q的幅度为1,两个信号互不相干,相位相差90度 ,是正交的。
图1
图2
极坐标图是观察幅度和相位的最好方法,载波是频率和相位的基准,信号表示为对载波的关系。信号可以以幅度和相位表示为极坐标的形式。相位是对基准信号而言的,基准信号一般是载波,幅度为绝对值或相对值。
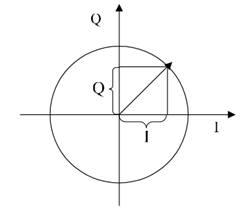
在数字通信中,通常以I、Q表示,极坐标中I轴在相位基准上,而Q轴则旋转90度。矢量信号在I轴上的投影为I分量,在Q轴上的投影为Q分量。图3显示I和Q的关系。
图3
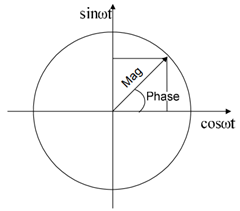
图 4 表示极坐标和直角坐标的转换。
图4
I、Q调制的主要优点是:既便于将两个独立信号分量组合成一个复合信号;相应地也可以将其复合信号分解为两个独立的部分。大多数数字调制是在I、Q平面上将数据映射为许多离散的点,我们称这些点为星座。当信号从一个点移向另一个点时,幅度调制和相位调制就同时完成了。I、Q信号分别是在X轴和Y轴上的投影,合成矢量的幅度表示载波的幅度,合成矢量与X轴的夹角表示载波相位。因此可以通过改变I 、Q驱动信号的幅度映射I-Q空间中的任意一点。在I 和Q信号传送的值只有预先定义的几个值,代表广泛不同的状态,一个调制的协议针对每个调制形式规定允许的状态数量。
QAM调制的基本原理
QAM调制实际上是幅度调制和相位调制的组合。相位 + 幅度状态定义了一个数字或数字的组合。QAM的优点是具有更大的符号率,从而可获得更高的系统效率。通常由符号率确定占用带宽。因此每个符号的比特(基本信息单位)越多,效率就越高。对于给定的系统,所需要的符号数为2n,这里n是每个符号的比特数。对于16QAM,n = 4,因此有16个符号,每个符号代表4 bit:0000, 0001,0010等。对于64QAM,n = 6,因此有64个符号,每个符号代表6bit:000000,000001,000010等。
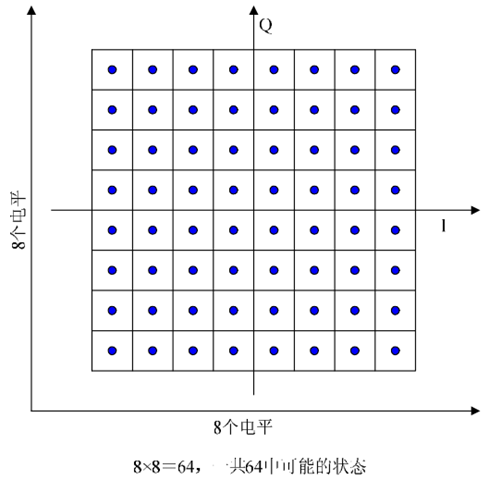
以上就是QAM调制的基本原理。经过信道编码的二进制的MPEG-2比特流进入QAM调制器,信号被分为两路,一路给I,另一路给Q,每一路一次给3比特的数据,这3比特的二进制数一共有8种不同的状态,分别对应8种不同的电平幅度,这样I有8个不同幅度的电平, Q有8个不同幅度的电平,而且I和Q两路信号正交。这样任意一个I的幅度和任意一个Q的幅度组合都会在极坐标图上映射一个相应的星座点,这样每个星座点代表由6个比特的数据组成的一个映射,I和Q一共有8×8共64种组合状态,各种可能出现过的数据状态组合最后映射到星座图上为图5所显示的64QAM星座图。
每一个星座点对应一个一定幅度和相位的模拟信号,这个模拟信号再被上变频到射频信号发射出去。这里再顺便说明一下模拟调制和数字调制的区别:模拟调制和数字调制之间的差别在于调制参数。在这两种方案中,改变的是载波信号的幅度、频率或相位(或是它们的组合)。在模拟调制中载波参数按连续的模拟信息信号改变,而在数字调制中,参数(幅度、频率或相位)按离散的数字信息改变。


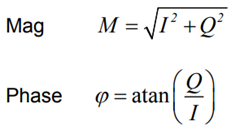

 浙公网安备 33010602011771号
浙公网安备 33010602011771号