Python实现熵值法确定权重

 本文从以下四个方面，介绍用Python实现熵值法确定权重：

一. 熵值法介绍

二. 熵值法实现

三. Python实现熵值法示例1

四. Python实现熵值法示例2

 

一. 熵值法介绍

熵值法是计算指标权重的经典算法之一，它是指用来判断某个指标的离散程度的数学方法。离散程度越大，即信息量越大，不确定性就越小，熵也就越小；信息量越小，不确定性越大，熵也越大。根据熵的特性，我们可以通过计算熵值来判断一个事件的随机性及无序程度，也可以用熵值来判断某个指标的离散程度，指标的离散程度越大，该指标对综合评价的影响越大。

 

二. 熵值法实现

1.假设数据有n行记录，m个变量，数据可以用一个n*m的矩阵A表示(n行m列，即n行记录数，m个特征列)

 

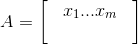
2.数据的归一化处理

xij表示矩阵A的第i行j列元素。

 

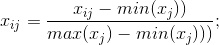
3.计算第j项指标下第i个记录所占比重

 

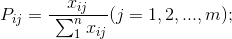
4.计算第j项指标的熵值

 

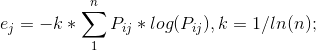
5.计算第j项指标的差异系数

 

6.计算第j项指标的权重

 

 

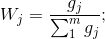
三. Python实现熵值法示例1

样例数据1

.csv格式数据内容

var1,var2,var3,var4,var5,var6
171.33,151.33,0.28,0,106.36,0.05
646.66,370,1.07,61,1686.79,1.64
533.33,189.66,0.59,0,242.31,0.57
28.33,0,0.17,0,137.85,2.29
620,234,0.88,41.33,428.33,0.13
192.33,177.66,0.16,0,128.68,1.07
111,94,0.18,0,234.27,0.22
291,654,1.21,65.66,2.26,0
421.33,247,0.7,0,0.4,0
193,288.66,0.16,0,0,0
82.33,118,0.11,0,758.41,0.24
649.66,648.66,0.54,0,13.35,0.11
37.66,103.33,0.12,0,1133.51,1.1
183.33,282.33,0.55,0,624.73,1.04
1014.66,1264.66,5.07,814.66,0,0
90.66,134,0.3,0,0.15,0
200.66,98.33,0.33,0,681.54,0.51
540.66,558.66,1.08,62,2.71,0.09
80,60.66,0.13,0,910.19,0.88
530.66,281.33,0.88,36,743.21,0.72
166,133,0.13,0,246.88,2.05
377.66,310.33,0.57,0,102.89,0.57
143.33,73,0.23,0,103.94,0.1
394.66,473.66,0.56,0,1.06,0.03
535.66,447.33,0.44,0,10.59,0.08
52.66,56.66,0.52,0,0,0
1381.66,760.66,2.3,781.66,248.71,0.13
44.33,42.33,0.07,0,0.66,0
71.66,62.66,0.11,0,535.26,0.52
148.33,56.66,0.24,0,173.83,0.16

Python代码:

#!/usr/bin/python
# -*- coding: utf-8 -*-
 
"""
Created on Fri Mar 23 10:48:36 2018
@author: Big Teacher Brother
"""
import pandas as pd
import numpy as np
import math
from numpy import array
 
# 1读取数据
df = pd.read_csv('E:\\text.csv', encoding='gb2312')
# 2数据预处理 ,去除空值的记录
df.dropna()
 
#定义熵值法函数
def cal_weight(x):
    '''熵值法计算变量的权重'''
    # 标准化
    x = x.apply(lambda x: ((x - np.min(x)) / (np.max(x) - np.min(x))))
 
    # 求k
    rows = x.index.size  # 行
    cols = x.columns.size  # 列
    k = 1.0 / math.log(rows)
 
    lnf = [[None] * cols for i in range(rows)]
 
    # 矩阵计算--
    # 信息熵
    # p=array(p)
    x = array(x)
    lnf = [[None] * cols for i in range(rows)]
    lnf = array(lnf)
    for i in range(0, rows):
        for j in range(0, cols):
            if x[i][j] == 0:
                lnfij = 0.0
            else:
                p = x[i][j] / x.sum(axis=0)[j]
                lnfij = math.log(p) * p * (-k)
            lnf[i][j] = lnfij
    lnf = pd.DataFrame(lnf)
    E = lnf
 
    # 计算冗余度
    d = 1 - E.sum(axis=0)
    # 计算各指标的权重
    w = [[None] * 1 for i in range(cols)]
    for j in range(0, cols):
        wj = d[j] / sum(d)
        w[j] = wj
        # 计算各样本的综合得分,用最原始的数据
    
    w = pd.DataFrame(w)
    return w
 
 
if __name__ == '__main__':
    # 计算df各字段的权重
    w = cal_weight(df)  # 调用cal_weight
    w.index = df.columns
    w.columns = ['weight']
    print(w)
    print('运行完成!')
 

运行的结果：

Running D:/tensorflow/ImageNet/shangzhifa.py
Backend Qt5Agg is interactive backend. Turning interactive mode on.
        weight
var1  0.088485
var2  0.074840
var3  0.140206
var4  0.410843
var5  0.144374
var6  0.141251
运行完成!

 

四. Python实现熵值法示例2

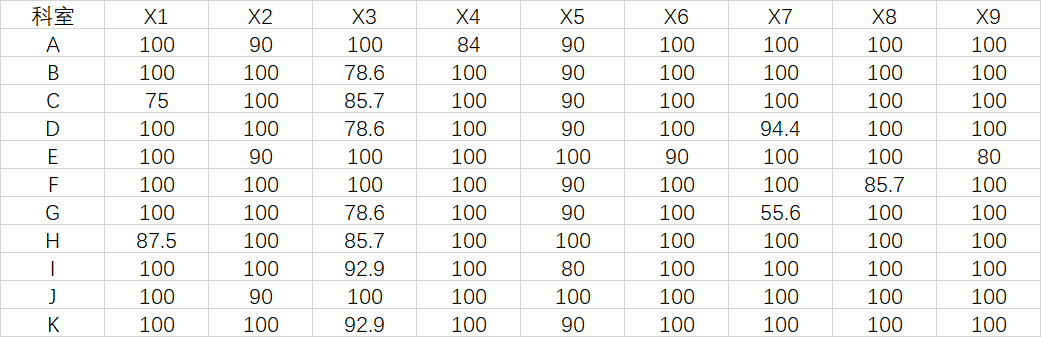
样例数据：

将数据保存到Excel表格中，并用xlrd读取。

Python代码：

import numpy as np
import xlrd
 
#读数据并求熵
path=u'K:\\选指标的.xlsx'
hn,nc=1,1
#hn为表头行数,nc为表头列数
sheetname=u'Sheet3'
def readexcel(hn,nc):
    data = xlrd.open_workbook(path)
    table = data.sheet_by_name(sheetname)
    nrows = table.nrows
    data=[]
    for i in range(hn,nrows):
        data.append(table.row_values(i)[nc:])
    return np.array(data)
def entropy(data0):
    #返回每个样本的指数
    #样本数，指标个数
    n,m=np.shape(data0)
    #一行一个样本，一列一个指标
    #下面是归一化
    maxium=np.max(data0,axis=0)
    minium=np.min(data0,axis=0)
    data= (data0-minium)*1.0/(maxium-minium)
    ##计算第j项指标，第i个样本占该指标的比重
    sumzb=np.sum(data,axis=0)
    data=data/sumzb
    #对ln0处理
    a=data*1.0
    a[np.where(data==0)]=0.0001
#    #计算每个指标的熵
    e=(-1.0/np.log(n))*np.sum(data*np.log(a),axis=0)
#    #计算权重
    w=(1-e)/np.sum(1-e)
    recodes=np.sum(data0*w,axis=1)
    return recodes
data=readexcel(hn,nc)
grades=entropy(data)

计算结果为：

In[32]:grades
Out[32]: 
array([95.7069621 , 93.14062354, 93.17273781, 92.77037549, 95.84064938,
       98.01005572, 90.20508545, 95.17203466, 95.96929203, 97.80841298,
       97.021269  ])

上面的程序计算得分时用了标准化前的值×权重，这对于原始评分量纲相同时没有什么问题。

按照论文上的公式，计算得分时应该用标准化后的值×权重，这对于原始数据量纲不同时应该这样做，因此按照论文的公式计算的程序如下：

Python代码为：

import numpy as np
import xlrd
 
#读数据并求熵
path=u'K:\\选指标的.xlsx'
hn,nc=1,1
#hn为表头行数,nc为表头列数
sheetname=u'Sheet3'
def readexcel(hn,nc):
    data = xlrd.open_workbook(path)
    table = data.sheet_by_name(sheetname)
    nrows = table.nrows
    data=[]
    for i in range(hn,nrows):
        data.append(table.row_values(i)[nc:])
    return np.array(data)
def entropy(data0):
    #返回每个样本的指数
    #样本数，指标个数
    n,m=np.shape(data0)
    #一行一个样本，一列一个指标
    #下面是归一化
    maxium=np.max(data0,axis=0)
    minium=np.min(data0,axis=0)
    data= (data0-minium)*1.0/(maxium-minium)
    ##计算第j项指标，第i个样本占该指标的比重
    sumzb=np.sum(data,axis=0)
    data=data/sumzb
    #对ln0处理
    a=data*1.0
    a[np.where(data==0)]=0.0001
#    #计算每个指标的熵
    e=(-1.0/np.log(n))*np.sum(data*np.log(a),axis=0)
#    #计算权重
    w=(1-e)/np.sum(1-e)
    recodes=np.sum(data*w,axis=1)
    return recodes
data=readexcel(hn,nc)
grades=entropy(data)

结果如下：

In[34]:grades
Out[34]: 
array([0.08767219, 0.07639727, 0.08342572, 0.07555273, 0.08920511,
       0.11506703, 0.06970125, 0.09550656, 0.09852824, 0.10232353,
       0.10662037])

参考文章：

https://blog.csdn.net/qq_24975309/article/details/82026022
https://blog.csdn.net/weixin_40450867/article/details/81226705
https://blog.csdn.net/weixin_41503009/article/details/82285422
https://blog.csdn.net/wangh0802/article/details/53981356
https://www.jianshu.com/p/3e08e6f6e244
https://blog.csdn.net/yang978897961/article/details/79164829/
https://blog.csdn.net/Yellow_python/article/details/83002698