ch01-导论

Ch01-导论

其中第一章可以快速阅读；

1.1 从游戏理论到决策理论

1. 博弈论解决的问题：有策略相互依存性的决策问题
2. 博弈论研究的博弈(game)的本质：特别是有策略互动和利益依存特征的（个人、队组或其他组织的）决策行为
3. 博弈论：是一种重视决策问题中策略互动性的决策理论。

这里以游戏为例

虽然在扑克游戏和体育竞技等游戏中，运气或身体素质的作用很大，但这些因素既定以后，策略选择好坏就是左右游戏结果的关键因素。 而且，策略选择也是游戏者可以自己把握的唯一因素。 更重要的一点是，许多游戏有策略相互依存的特征。 即每一个游戏者所得结果的好坏，不仅取决于自身的策略选择，也取决于其他参加者的策略选择。

有时差的策略选择会带来并不差的结果，原因是其他游戏者选择了更差的策略，意味着策略本身往往没有绝对的好坏之分，优劣关系是相对于对手的策略而 言的。

1.2 一些例子

古诺纳什均衡？

1. 博弈方(players)
2. 策略(strategies)
3. 得益(payoffs)
4. 得益矩阵(payoff matrix)

对于个体而言，最优的选择不一定会带来对个体或者对整体而言最优的结果

1.3 博弈的特征和博弈的分类

1.3.1 博弈方

博弈问题最基本的方面是博弈参加者，也称为“ 博弈方" (players) , 即在博弈中独立决策、独立承担结果的个人或组织。 博弈的根本特征是策略依存性。 博弈方数量越多，策略依存性越复杂 ，分析就越困难。 因 此，博弈方数量是博弈结构的关键参数之一。

根据博弈方的数量 ，可以将博弈分为“单人博弈" 、“两人博弈”和 “多人博弈"。

单人博弈即只有一个博弈方的博弈。 单人博弈不存在其他博弈方的反应和反作用，因此比较简单。 事实上单人博弈已经退化为一般的最优 化问题。

不过讨论单人博弈还是有价值的，因为包括单人博弈可以使博弈理论结构更加完整，而且两人、多人博弈常要转化为多个、多层次的单人博弈进行分析。

case1：单人迷宫游戏

单人迷宫游戏是最简单的单人博弈问题。 其中 ， 游戏者面临的问题是：如果从入口处进入迷宫后，能不走任何回头路而顺利到达出口 ， 就能获得奖金M, 否则得不到任何奖金。

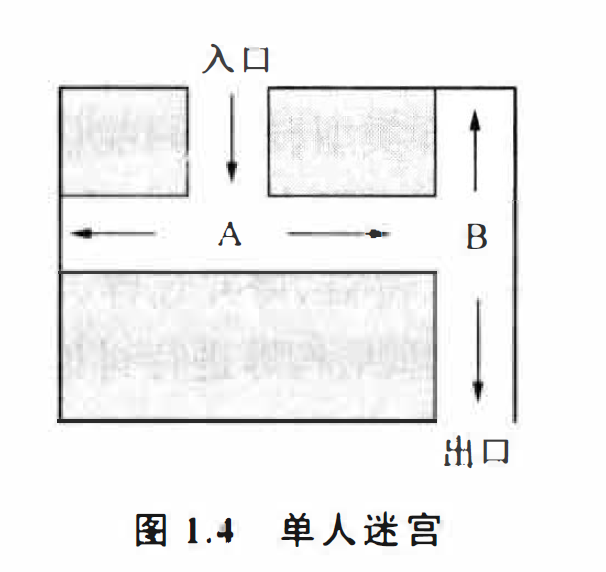
作为一个博弈问题，它的几个方面规定如下：

1. 该博弈中有唯一的博弈方，即游戏者；

2. 该博弈方有"A处左转，B处左转” 、"A处左转 ， B处右转”、"A处右转，B处左转”、"A处右转，B处右转“四种可供选择的策略；

3. 因为只有一个博弈方，因此不存在与其他博弈方选择、行动的先后次序问题；

4. 如果得奖金M算得益M,得不到奖金算得益0，则匹种策略对应的得益分别为 0、 M 、 0 、 0 。

当游戏者事先对四种策略对应的得益很清楚，因此在A、 B两处能对哪边走得通、哪边走不通作出准确判断时，该博弈的解简单明了，即他必然会选择"A处左转，B处右转＂的策略，顺利走出迷宫，并取得得益（即奖金）M。