215. 数组中的第K个最大元素(快速排序)

215. 数组中的第K个最大元素

思路：

快速排序

3.8 快速排序

算法描述

算法思想: 对给定数组中的元素进行重新排列, 确定数组中元素的一个位置q, 得到一个快速排序的划分

QUICKSORT功能，将数组A的A[p]到A[q]变为有序(比如从小到大)

QUICKSORT(A, p, r)

1. if p < r
2. then q \(\leftarrow\) PARTITION(A, p, r)
3. ​ QUICKSORT(A, p, q)
4. ​ QUICKSORT(A, q + 1, r)

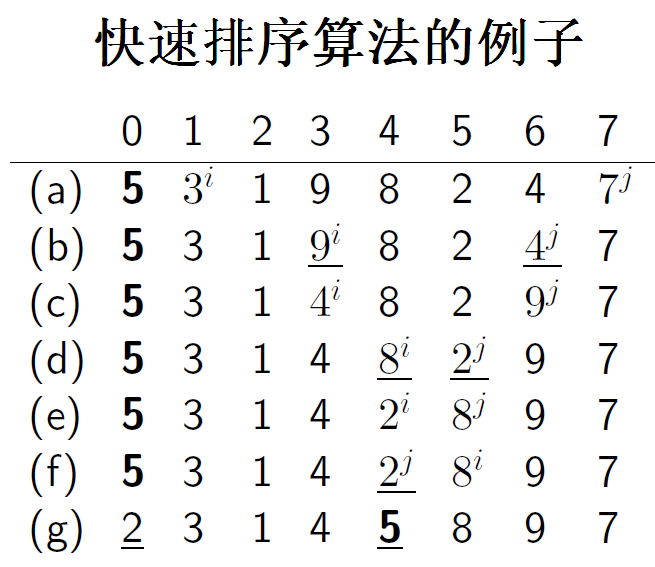
PARTITION在A[p]到A[r]以A[p]为界划分成两部分A[p]的左边比A[p]小，A[p]的右边比A[p]大

PARTITION(A, p, r)

1. x \(\leftarrow\) A[p], i \(\leftarrow\) p + 1, j \(\leftarrow\) r
2. while i \(\leq\) j
3. while A[j] \(\geq\) x and j \(>\) p
4. j \(\leftarrow\) j -1
5. while A[i] \(\leq\) x and i \(<\) r
6. i \(\leftarrow\) i + 1
7. if i < j then A[i] \(\leftrightarrow\) A[j]
8. i \(\leftarrow\) i + 1, j \(\leftarrow\) j - 1
9. A[p] $ A[j], return j

(1)快速排序算法复杂性分析

快速排序算法的运行时间依赖于:

• 划分的平衡与否
• 划分的平衡与否依赖于算法的输入
• 如果划分平衡, 时间复杂性为\(O(n log n)\)
• 如果划分不平衡, 时间复杂性为\(O(n^2)\)

最坏时间复杂性

Quicksort 的最坏情况发生在Partition 输出的两个区域中, 一个仅包含1 个元素, 另一个包含n - 1个元素的情况;假设上述不平衡的划分发生在算法的每一步迭代中, 则

排序过程中每次都出现上述情况就是最坏情况

\[T(n) = \begin{cases} O(1)&\text{,n} \leq {1}\\[2ex] T(n - 1) + O(n)&\text{,n > 1}\\[2ex] \end{cases} \]

每次问题的规模只减小了1，易知时间复杂度为\(O(n^2)\)

最优时间复杂性

设如果Partition 算法产生两个大小为n=2 的区域,则

\[T(n) = 2T(\frac{n}{2}) + O(n) \]

根据主定理, 可以得出

\[T(n) = O(n log n) \]

(2)随机化快速排序算法

• 快速排序算法取决于划分的对称性
• 采用随机策略进行划分
• 算法每一步在数组A[p, r] 中随机选出一个元素作为划分元素, 可以期望划分是较对称的

RANDOMIZED-QUICKSORT算法

RANDOMIZED-QUICKSORT(A, p, r)

1. if p < r
2. then q =RANDOMIZED-PATITION(A, p, r)
3. ​ RANDOMIZED-QUICKSORT(A, p, q)
4. ​ RANDOMIZED-QUICKSORT(A, q + 1, r)

RANDOMIZED-PARTITION算法

RANDOMIZED-PARTITION(A, p, r)

1. ​ i=Random(p, r)
2. ​ exchange A[p] \(\leftrightarrow\) A[i]
3. ​ Return PARTITION(A, p, r)

代码如下：

package main

import (
	"fmt"
	"math/rand"
)

func findKthLargest(nums []int, k int) int {
	left := 0
	right := len(nums)-1
	length :=len(nums)-k

	for{
		if left == right{// 循环终止条件
			return nums[right]
		}
		p := partition(nums,left,right)
		if p == length{
			return nums[p]
		}else if p<length{
			left = p+1
		}else{
			right = p-1
		}
	}

}
func partition(nums []int,left int,right int)( int){
	// 产生一个随机数
	randlf := right -left
	rand_get := rand.Intn(randlf)
	rand_fin := left+rand_get

	// 将产生的随机数对应的数组中的元素和num[left]互换
	randnum :=rand_fin
	temp_1 :=nums[randnum]
	temp_2 := nums[left]
	nums[left],nums[randnum] = temp_1,temp_2

	x := nums[left]
	i := left+1
	j := right
	for i<=j{
		for nums[j]>=x && j>left{
			j = j-1
		}
		for nums[i]<=x && i<right{
			i = i+1
		}
		if i<j{
			temp := nums[i]
			nums[i],nums[j] = nums[j],temp
			i = i+1
			j = j-1
		}
	}
	t := nums[left]
	nums[left],nums[j] = nums[j],t
	return j
}

func main(){
	nums := []int{1,2,4,5,6,7,8}
	fmt.Println(findKthLargest(nums,2))

}