归并排序(leetcode148)
148. 排序链表
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
进阶:
- 你可以在
O(n log n)时间复杂度和常数级空间复杂度下,对链表进行排序吗?
示例 1:

输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:
输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
提示:
- 链表中节点的数目在范围
[0, 5 * 104]内 -105 <= Node.val <= 105
题解
思路
看到时间复杂度的要求,而且是链表,归并排序比较好做。
都知道归并排序要先归(二分),再并。两个有序的链表是才比较容易合并的。
二分到不能再二分,即递归压栈到了底部,链只有一个结点,本身就是有序的,于是在递归出栈时进行合并。
// 伪代码
func sortList (head) {
对链表进行二分
l = sortList(左链) // 已排序的左链
r = sortList(右链) // 已排序的右链
merged = mergeList(l, r) // 进行合并
return merged // 返回合并的结果给父调用
}
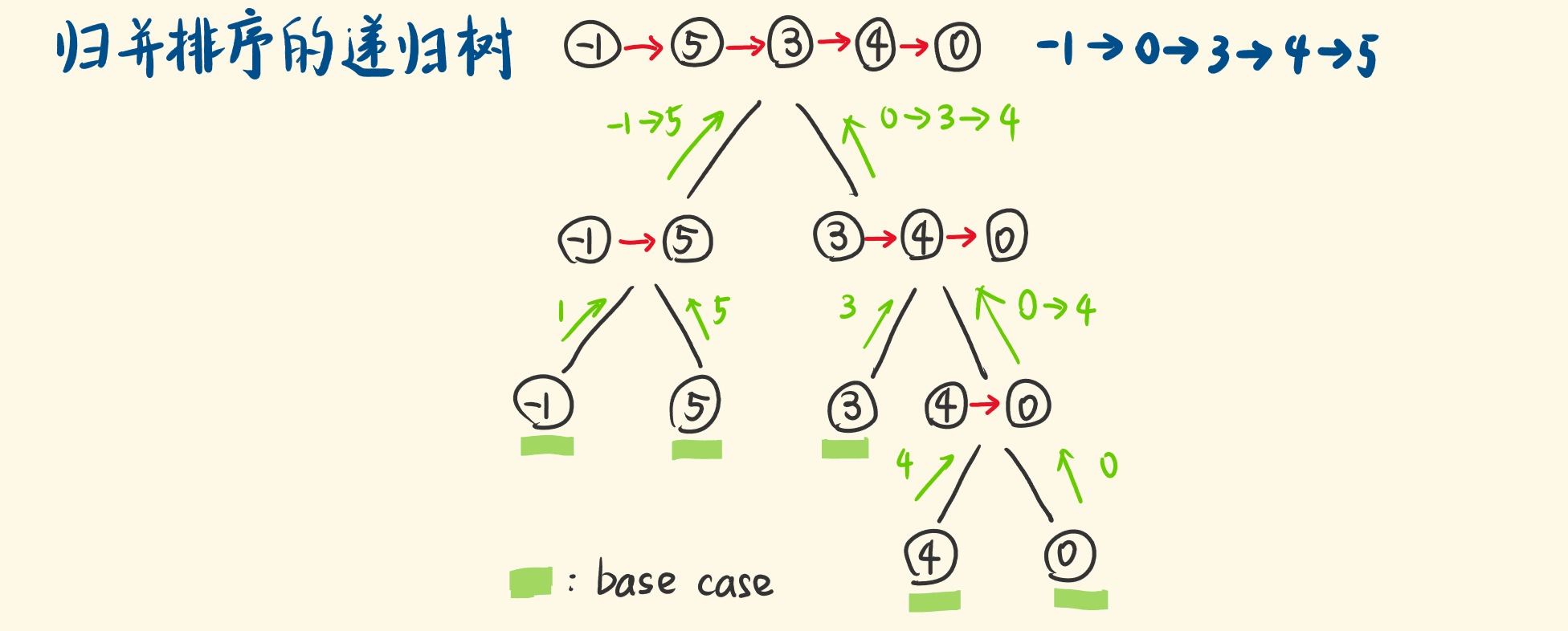
二分、merge 函数
-
二分,用快慢指针法,快指针走两步,慢指针走一步,快指针越界时,慢指针正好到达中点,只需记录慢指针的前一个指针,就能断成两链。
-
merge 函数做的事是合并两个有序的左右链
-
设置虚拟头结点,用 prev 指针去“穿针引线”,prev 初始指向 dummy
-
每次都确定 prev.Next 的指向,并注意 l1 / l2指针的推进,和 prev 指针的推进
-
最后返回 dummy.Next ,即合并后的链。
-

代码实现(golang)
节点的定义:
//Definition for singly-linked list.
type ListNode struct {
Val int
Next *ListNode
}
MERGESORT:
// 把无序数组变为有序数组
func sortList(head *ListNode) *ListNode {
if head == nil || head.Next == nil { // 递归的出口,不用排序 直接返回
return head
}
slow, fast := head, head // 快慢指针
var preSlow *ListNode // 保存slow的前一个结点
for fast != nil && fast.Next != nil {
preSlow = slow
slow = slow.Next // 慢指针走一步
fast = fast.Next.Next // 快指针走两步
}
preSlow.Next = nil // 断开,分成两链
// 分治,把左边的无序数组变为有序数组
l := sortList(head) // 已排序的左链
// 分治,把右边的边的无序数组变为有序数组
r := sortList(slow) // 已排序的右链
return mergeList(l, r) // 合并已排序的左右链,一层层向上返回
}
MERGE
两种写法:
-
循环实现分治
// 非递归写法 func mergeList(l1, l2 *ListNode) *ListNode { dummy := &ListNode{Val: 0} // 虚拟头结点 prev := dummy // 用prev去扫,先指向dummy for l1 != nil && l2 != nil { // l1 l2 都存在 if l1.Val < l2.Val { // l1值较小 prev.Next = l1 // prev.Next指向l1 l1 = l1.Next // 考察l1的下一个结点 } else { prev.Next = l2 l2 = l2.Next } prev = prev.Next // prev.Next确定了,prev指针推进 } if l1 != nil { // l1存在,l2不存在,让prev.Next指向l1 prev.Next = l1 } if l2 != nil { prev.Next = l2 } return dummy.Next // 真实头结点 } -
递归实现分治
// 递归写法,l1,l2均为有序数组,将两个有序数组合并为1个有序数组 func mergeList(l1, l2 *ListNode) *ListNode { if l1==nil { return l2 } if l2==nil { return l1 } if l1.Val > l2.Val{ l2.Next = mergeList(l1, l2.Next) return l2 } l1.Next = mergeList(l2, l1.Next) return l1 }
MERGE和MERGESORT的算法描述
MERGESORT(A)
- if len(A) <= 1 return A
- q \(\leftarrow\) \(\frac{len(A)}{2}\)
- L \(\leftarrow\) A[0...q], R \(\leftarrow\) A[q + 1...len(A) - 1]
- L \(\leftarrow\) MERGESORT(L)
- R \(\leftarrow\) MERGESORT(R)
- return MERGE(L,R)
MERGE(L,R)
- i \(\leftarrow\) 0; j \(\leftarrow\) 0; aux \(\leftarrow\) [ ]
- while i < len(L) and j < len(R)
- if L[i] \(\leq\) R[j]
- aux:add(L[i]) ; i \(\leftarrow\) i + 1
- else aux:add(R[j]) ; j \(\leftarrow\) j + 1
- if i == len(L)
- aux.add(R[j : len(R) - 1])
- else aux.add(L[i : len(L) - 1])
- return


