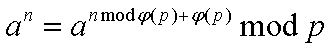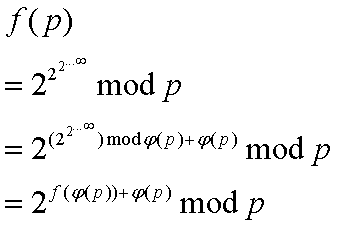P4139 上帝与集合的正确用法

本题是欧拉定理的应用。我这种蒟蒻当然不知道怎么证明啦！

那么我们就不证明了，来直接看结论:

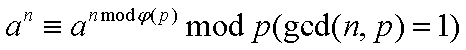
这里写图片描述

a b \equiv ⎧ ⎩ ⎨ ⎪ ⎪

这里写图片描述 $a^{b} \equiv {\begin{cases} a^{b % ϕ (p)} g c d (a, p) = 1 \\ a^{b} g c d (a, p) \neq 1, b < ϕ (p) \\ a^{b % ϕ (p) + ϕ (p)} g c d (a, p) \neq 1, b \geq ϕ (p) \end{cases} (m o d p)$ $a^{b} \equiv {\begin{cases} a^{b % ϕ (p)} g c d (a, p) = 1 \\ a^{b} g c d (a, p) \neq 1, b < ϕ (p) \\ a^{b % ϕ (p) + ϕ (p)} g c d (a, p) \neq 1, b \geq ϕ (p) \end{cases} (m o d p)$

$a^{b} \equiv {\begin{cases} a^{b % ϕ (p)} g c d (a, p) = 1 \\ a^{b} g c d (a, p) \neq 1, b < ϕ (p) \\ a^{b % ϕ (p) + ϕ (p)} g c d (a, p) \neq 1, b \geq ϕ (p) \end{cases} (m o d p)$

$a^{b} \equiv {\begin{cases} a^{b % ϕ (p)} g c d (a, p) = 1 \\ a^{b} g c d (a, p) \neq 1, b < ϕ (p) \\ a^{b % ϕ (p) + ϕ (p)} g c d (a, p) \neq 1, b \geq ϕ (p) \end{cases} (m o d p)$ $a^{b} \equiv {\begin{cases} a^{b % ϕ (p)} g c d (a, p) = 1 \\ a^{b} g c d (a, p) \neq 1, b < ϕ (p) \\ a^{b % ϕ (p) + ϕ (p)} g c d (a, p) \neq 1, b \geq ϕ (p) \end{cases} (m o d p)$

或者观看这个

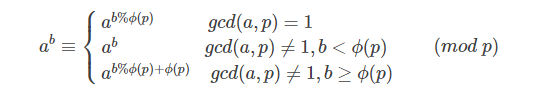
那么再来看本题，主要使用了后者：

这里写图片描述

所以可以写出递归式：

f(p)=qpow(2,f(ask_phi(p))+ask_phi(p),p);

得解。

题外话：我本来先打个表求出10^7以内的phi[]，然后直接调用的，结果全T...

发现n<=1000，就用了ask_phi()，然后就过了。

 1 #include <cstdio>
 2 using namespace std;
 3 const int N = 10000010;
 4 typedef long long LL;
 5 
 6 LL phi[N];
 7 
 8 void make_phi(int n)
 9 {
10     for(int i=1;i<=n;i++) phi[i]=i;
11     for(int i=2;i<=n;i+=2) phi[i]/=2;
12     for(int i=3;i<=n;i+=2)
13     {
14         if(phi[i]==i)
15         {
16             for(int j=i;j<=n;j+=i) phi[j]=(phi[j]/i)*(i-1);
17         }
18     }
19     return;
20 }
21 
22 LL ask_phi(int x)
23 {
24     LL ans=x;
25     for(int i=2;i*i<=x;i++)
26     {
27         if(x%i==0)
28         {
29             while(x%i==0) x/=i;
30             ans=(ans/i)*(i-1);
31         }
32     }
33     if(x>1) ans=(ans/x)*(x-1);
34     return ans;
35 }
36 
37 LL qpow(LL a,LL b,LL m)
38 {
39     LL ans=1;
40     while(b)
41     {
42         if(b&1) ans=(ans*a)%m;
43         b=b>>1;
44         a=(a*a)%m;
45     }
46     return ans;
47 }
48 
49 LL f(int p)
50 {
51     if(p==1) return 0;
52     return qpow(2,f(ask_phi(p))+ask_phi(p),p);
53 }
54 
55 int main()
56 {
57     int n,x;
58     scanf("%d",&n);
59     //make_phi(N);
60     while(n--)
61     {
62         scanf("%d",&x);
63         printf("%lld\n",f(x));
64     }
65     return 0;
66 }

AC代码

我们学到了什么姿势：

1.欧拉函数：φ(n)=[1,n]中与n互质的数的个数。

求phi(x):

 1 LL ask_phi(int x)
 2 {
 3     LL ans=x;
 4     for(int i=2;i*i<=x;i++)
 5     {
 6         if(x%i==0)
 7         {
 8             while(x%i==0) x/=i;
 9             ans=(ans/i)*(i-1);
10         }
11     }
12     if(x>1) ans=(ans/x)*(x-1);
13     return ans;
14 }

ask_phi()

打表phi[]：

 1 void make_phi(int n)
 2 {
 3     for(int i=1;i<=n;i++) phi[i]=i;
 4     for(int i=2;i<=n;i+=2) phi[i]/=2;
 5     for(int i=3;i<=n;i+=2)
 6     {
 7         if(phi[i]==i)
 8         {
 9             for(int j=i;j<=n;j+=i) phi[j]=(phi[j]/i)*(i-1);
10         }
11     }
12     return;
13 }

make_phi()

二进制快速幂：

 1 LL qpow(LL a,LL b,LL m)
 2 {
 3     LL ans=1;
 4     while(b)
 5     {
 6         if(b&1) ans=(ans*a)%m;
 7         b=b>>1;
 8         a=(a*a)%m;
 9     }
10     return ans;
11 }