BZOJ4036 按位或

解：有两种做法......

第一种，按照秘密袭击coat的套路，我们只需要求出即可。因为一种操作了i次的方案会被恰好计数i次。

那么这个东西怎么求呢？直接用FWT的思想，对于一个状态s，求出选择s所有子集的概率p_s。那么第i次操作后是s的子集的概率就是p_sⁱ。

设f_s表示第i次操作之后是s的子集的概率。

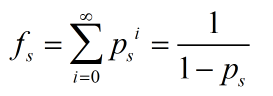
把所有的f求出来之后做一次IFWT即可。然后我们对于所有非全集求和。

 1 #include <bits/stdc++.h>
 2 
 3 const int N = 30, M = 1500010;
 4 const double eps = 1e-12;
 5 
 6 double f[M], p[M], w[M];
 7 int cnt[M], pw[M], n, lm;
 8 
 9 inline void FWT_or(double *a, int n, int f) {
10     for(int len = 1; len < n; len <<= 1) {
11         for(int i = 0; i < n; i += (len << 1)) {
12             for(int j = 0; j < len; j++) {
13                 a[i + len + j] += f * a[i + j];
14             }
15         }
16     }
17     return;
18 }
19 
20 int main() {
21     scanf("%d", &n);
22     lm = 1 << n;
23     for(int i = 0; i < lm; i++) {
24         scanf("%lf", &p[i]);
25         w[i] = p[i];
26         if(i) {
27             cnt[i] = 1 + cnt[i - (i & (-i))];
28         }
29         if(i > 1) {
30             pw[i] = pw[i >> 1] + 1;
31         }
32     }
33     FWT_or(p, lm, 1);
34     for(int i = 0; i < lm; i++) {
35         if(i != lm - 1 && p[i] > 1 - eps) {
36             puts("INF");
37             return 0;
38         }
39         f[i] = 1.0 / (1 - p[i]);
40     }
41     FWT_or(f, lm, -1);
42     double ans = 0;
43     for(int i = 0; i < lm - 1; i++) {
44         ans += f[i];
45     }
46     printf("%.10f\n", ans);
47     return 0;
48 }

AC代码

第二种：Min-Max容斥。

设f_s为把状态s的所有元素中至少一个变成1的期望次数。

同样是对步数0~∞求和，每次的概率是(没选到)ⁱ。最后Min-Max容斥统计答案。

 1 #include <bits/stdc++.h>
 2 
 3 const int N = 30, M = 1500010;
 4 const double eps = 1e-12;
 5 
 6 double f[M], p[M], w[M];
 7 int cnt[M], pw[M], n, lm;
 8 
 9 inline void FWT_or(double *a, int n, int f) {
10     for(int len = 1; len < n; len <<= 1) {
11         for(int i = 0; i < n; i += (len << 1)) {
12             for(int j = 0; j < len; j++) {
13                 a[i + len + j] += f * a[i + j];
14             }
15         }
16     }
17     return;
18 }
19 /*
20 2
21 0.25 0.25 0.25 0.25
22 
23 */
24 int main() {
25     scanf("%d", &n);
26     lm = 1 << n;
27     for(int i = 0; i < lm; i++) {
28         scanf("%lf", &p[i]);
29         w[i] = p[i];
30         if(i) {
31             cnt[i] = 1 + cnt[i - (i & (-i))];
32         }
33         if(i > 1) {
34             pw[i] = pw[i >> 1] + 1;
35         }
36     }
37     FWT_or(p, lm, 1);
38     for(int i = 0; i < lm; i++) {
39         if(i != lm - 1 && p[i] > 1 - eps) {
40             printf("INF\n");
41             return 0;
42         }
43         //printf("p %d = %lf \n", i, p[i]);
44         f[i] = 1.0 / (1 - p[(lm - 1) ^ i]);
45     }
46     //FWT_or(f, lm, -1);
47     double ans = 0;
48     for(int i = 1; i < lm; i++) {
49         if(cnt[i] & 1) ans += f[i];
50         else ans -= f[i];
51     }
52     printf("%.10f\n", ans);
53     return 0;
54 }