CF1101F Trucks and Cities

题意：给定线段上n个特殊点，m次询问。

每次询问：在第l个点到第r个点这一段区间中选出k个点，将其分成k + 1段。使得最长的段尽量短。

输出这m个询问中答案最大的。 n<=400,m<=250000

解：显然有个暴力DP是n⁴的。f[l][r][k]表示把[l, r]分成k段的最短长度。

然后我们发现一件事：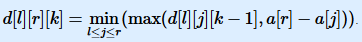

考虑j增加的时候，这个东西左半边单增，右半边单减。于是这个东西对于j是个凸的。

还发现r增大的时候，j一定不会减少。

然后枚举l和k，r递增的同时让一个指针j跟着增加。这样就是n³DP了。

 1 #include <bits/stdc++.h>
 2 
 3 typedef long long LL;
 4 const int N = 405;
 5 
 6 int f[N][N][N], a[N];
 7 
 8 int main() {
 9     int n, m;
10     scanf("%d%d", &n, &m);
11     for(int i = 1; i <= n; i++) {
12         scanf("%d", &a[i]);
13     }
14 
15     for(int l = 1; l <= n; l++) {
16         for(int r = l; r <= n; r++) {
17             f[l][r][0] = a[r] - a[l];
18         }
19     }
20 
21     for(int l = 1; l < n; l++) {
22         for(int k = 1; k <= n; k++) {
23             int p = l + 1;
24             for(int r = l + 2; r <= n; r++) {
25                 while(p < r - 1 && std::max(f[l][p][k - 1], a[r] - a[p]) >= std::max(f[l][p + 1][k - 1], a[r] - a[p + 1])) {
26                     p++;
27                 }
28                 f[l][r][k] = std::max(f[l][p][k - 1], a[r] - a[p]);
29             }
30         }
31     }
32 
33     LL ans = 0;
34     for(int i = 1, l, r, c, k; i <= m; i++) {
35         scanf("%d%d%d%d", &l, &r, &c, &k);
36         ans = std::max(ans, 1ll * c * f[l][r][k]);
37     }
38     printf("%lld\n", ans);
39     return 0;
40 }