LOJ#2541 猎人杀

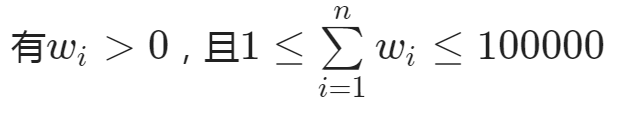
解：step1：猎人死了之后不下台，而是继续开枪，这样分母不变......

然后容斥，枚举猎人集合s，钦定他们在1之后死。定义打到1的时候结束，枚举游戏在i轮时结束。

发现式子是一个1 + x + x² + x³ + ... = 1 / (1 - x)

但是枚举子集不现实，发现值域很小，我们用小Z的礼物的套路，考虑计算每个值的容斥系数是多少。

然后就NTT加速了。预处理逆元卡常。

  1 #include <bits/stdc++.h>
  2 
  3 typedef long long LL;
  4 typedef std::vector<int> Poly;
  5 
  6 inline void read(int &x) {
  7     x = 0;
  8     char c = getchar();
  9     while(c < '0' || c > '9') c = getchar();
 10     while(c >= '0' && c <= '9') {
 11         x = x * 10 + c - 48;
 12         c = getchar();
 13     }
 14     return;
 15 }
 16 
 17 const int N = 200010, MO = 998244353;
 18 
 19 int A[N << 2], B[N << 2];
 20 int r[N << 2], n, w[N], inv[N];
 21 
 22 inline int qpow(int a, int b) {
 23     a = (a % MO + MO) % MO;
 24     int ans = 1;
 25     while(b) {
 26         if(b & 1) ans = 1ll * ans * a % MO;
 27         a = 1ll * a * a % MO;
 28         b = b >> 1;
 29     }
 30     return ans;
 31 }
 32 
 33 inline void prework(int n) {
 34     static int R = 0;
 35     if(R == n) return;
 36     R = n;
 37     int lm = 1;
 38     while((1 << lm) < n) lm++;
 39     for(register int i = 0; i < n; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (lm - 1));
 40     return;
 41 }
 42 
 43 inline void NTT(int *a, int n, int f) {
 44     prework(n);
 45     for(int i = 0; i < n; i++) {
 46         if(i < r[i]) std::swap(a[i], a[r[i]]);
 47     }
 48     for(register int len = 1; len < n; len <<= 1) {
 49         int Wn = qpow(3, (MO - 1) / (len << 1));
 50         if(f == -1) Wn = qpow(Wn, MO - 2);
 51         for(register int i = 0; i < n; i += (len << 1)) {
 52             int w = 1;
 53             for(register int j = 0; j < len; j++) {
 54                 int t = 1ll * a[i + len + j] * w % MO;
 55                 a[i + len + j] = (a[i + j] - t) % MO;
 56                 a[i + j] = (a[i + j] + t) % MO;
 57                 w = 1ll * w * Wn % MO;
 58             }
 59         }
 60     }
 61     if(f == -1) {
 62         LL inv = qpow(n, MO - 2);
 63         for(int i = 0; i < n; i++) {
 64             a[i] = 1ll * a[i] * inv % MO;
 65         }
 66     }
 67     return;
 68 }
 69 
 70 inline Poly mul(const Poly &a, const Poly &b) {
 71     int na = a.size(), nb = b.size(), n = na + nb - 1, len = 1;
 72     while(len < n) len <<= 1;
 73     for(register int i = 0; i < na; i++) A[i] = a[i];
 74     for(register int i = 0; i < nb; i++) B[i] = b[i];
 75     memset(A + na, 0, (len - na) * sizeof(LL));
 76     memset(B + nb, 0, (len - nb) * sizeof(LL));
 77     NTT(A, len, 1); NTT(B, len, 1);
 78     for(register int i = 0; i < len; i++) A[i] = 1ll * A[i] * B[i] % MO;
 79     NTT(A, len, -1);
 80     Poly ans(n);
 81     for(register int i = 0; i < n; i++) ans[i] = A[i];
 82     return ans;
 83 }
 84 
 85 Poly solve(int l, int r) {
 86     if(l == r) {
 87         Poly a(w[r] + 1);
 88         a[0] = 1; a[w[r]] = -1;
 89         return a;
 90     }
 91     int mid = (l + r) >> 1;
 92     return mul(solve(l, mid), solve(mid + 1, r));
 93 }
 94 
 95 int main() {
 96     int sum = 0;
 97     read(n);
 98     for(register int i = 1; i <= n; i++) {
 99         read(w[i]);
100         sum += w[i];
101     }
102 
103     inv[0] = inv[1] = 1;
104     for(int i = 2; i <= sum; i++) {
105         inv[i] = 1ll * inv[MO % i] * (MO - MO / i) % MO;
106     }
107 
108     std::sort(w + 2, w + n + 1);
109     Poly a = solve(2, n);
110 
111     int m = a.size();
112     int ans = 0;
113     for(register int i = 0; i < m; i++) {
114         ans = (ans + 1ll * a[i] * inv[w[1] + i] % MO) % MO;
115     }
116     ans = 1ll * ans * w[1] % MO;
117     printf("%d\n", (ans + MO) % MO);
118     return 0;
119 }