51nod1238 最小公倍数之和 V3

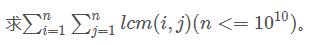
又被这神仙题给坑爆了。

神仙题解。

一开始我把lcm变成ij/gcd然后按照常规套路去推，推到最后发现不是miu * Id而是miu · Id......这还搞鬼啊。

正解居然跟这个差不多，先转成求其中一部分的函数，然后再加和......这谁顶得住呀。

大概就是先求这个

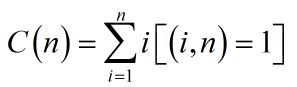
一顿操作之后得到了phi有关的式子......

然后原式就是这个

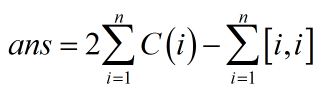
然后带进去推一推就出来杜教筛了...这第一步真是神奇。

最后是这个。

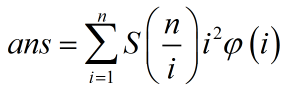
按照套路，前面分块，后面配一个g(x) = x²即可。

 1 #include <cstdio>
 2 #include <map>
 3 
 4 typedef long long LL;
 5 const int N = 5000010, T = 5000008;
 6 const LL MO = 1000000007;
 7 
 8 std::map<LL, LL> mp;
 9 LL inv2, inv6, F[N];
10 int p[N], top, phi[N];
11 bool vis[N];
12 
13 inline LL qpow(LL a, LL b) {
14     LL ans = 1;
15     while(b) {
16         if(b & 1) ans = ans * a % MO;
17         a = a * a % MO;
18         b = b >> 1;
19     }
20     return ans;
21 }
22 
23 inline LL S(LL x) {
24     x %= MO;
25     return x * (x + 1) / 2 % MO;
26 }
27 
28 inline LL G(LL x) {
29     x %= MO;
30     return (x << 1 | 1) % MO * (x + 1) % MO * x % MO * inv6 % MO;
31 }
32 
33 inline LL H(LL x) {
34     LL temp = S(x);
35     return temp * temp % MO;
36 }
37 
38 inline void getp(int n) {
39     phi[1] = 1;
40     for(int i = 2; i <= n; i++) {
41         if(!vis[i]) {
42             p[++top] = i;
43             phi[i] = i - 1;
44         }
45         for(int j = 1; j <= top && i * p[j] <= n; j++) {
46             vis[i * p[j]] = 1;
47             if(i % p[j] == 0) {
48                 phi[i * p[j]] = phi[i] * p[j];
49                 break;
50             }
51             phi[i * p[j]] = phi[i] * (p[j] - 1);
52         }
53     }
54     for(int i = 1; i <= n; i++) {
55         F[i] = (F[i - 1] + 1ll * i * i % MO * phi[i] % MO) % MO;
56     }
57     return;
58 }
59 
60 LL getF(LL x) {
61     if(x <= 0) return 0;
62     if(x <= T) return F[x];
63     if(mp.count(x)) return mp[x];
64     LL ans = H(x);
65     for(LL i = 2, j; i <= x; i = j + 1) {
66         j = x / (x / i);
67         ans -= (G(j) - G(i - 1) + MO) * getF(x / i) % MO;
68         ans %= MO;
69     }
70     return mp[x] = (ans + MO) % MO;
71 }
72 
73 int main() {
74     inv2 = (MO + 1) / 2;
75     inv6 = qpow(6, MO - 2);
76     getp(T);
77     LL ans = 0, n;
78     scanf("%lld", &n);
79     for(LL i = 1, j; i <= n; i = j + 1) {
80         j = n / (n / i);
81         ans += S(n / i) * (getF(j) - getF(i - 1) + MO) % MO;
82         ans %= MO;
83     }
84     printf("%lld\n", (ans + MO) % MO);
85     return 0;
86 }