51nod1237 最大公约数之和 V3

题意：求

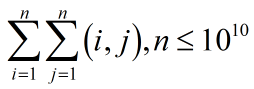
解：

最后一步转化是因为phi * I = Id，故Id * miu = phi

第二步是反演，中间省略了几步...

然后就这样A了......最终式子是个整除分块，后面用杜教筛求一下phi前缀和即可。

 1 #include <cstdio>
 2 #include <map>
 3 
 4 typedef long long LL;
 5 const int N = 5000010, T = 5000008;
 6 const LL MO = 1000000007;
 7 
 8 int p[N], top, phi[N];
 9 LL Phi[N], inv2;
10 bool vis[N];
11 std::map<LL, LL> mp;
12 
13 inline void getp(int n) {
14     phi[1] = 1;
15     for(int i = 2; i <= n; i++) {
16         if(!vis[i]) {
17             p[++top] = i;
18             phi[i] = i - 1;
19         }
20         for(int j = 1; j <= top && i * p[j] <= n; j++) {
21             vis[i * p[j]] = 1;
22             if(i % p[j] == 0) {
23                 phi[i * p[j]] = phi[i] * p[j];
24                 break;
25             }
26             phi[i * p[j]] = phi[i] * (p[j] - 1);
27         }
28     }
29     for(int i = 1; i <= n; i++) {
30         Phi[i] = (Phi[i - 1] + phi[i]) % MO;
31     }
32     return;
33 }
34 
35 LL getPhi(LL x) {
36     if(x <= 0) return 0;
37     if(x <= T) return Phi[x];
38     if(mp.count(x)) return mp[x];
39     LL ans = (x + 1) % MO * (x % MO) % MO * inv2 % MO;
40     for(LL i = 2, j; i <= x; i = j + 1) {
41         j = x / (x / i);
42         ans -= (j - i + 1) % MO * getPhi(x / i) % MO;
43         ans %= MO;
44     }
45     return mp[x] = (ans + MO) % MO;
46 }
47 
48 int main() {
49     LL n;
50     getp(T);
51     inv2 = (MO + 1) / 2;
52     scanf("%lld", &n);
53     LL ans = 0;
54     for(LL i = 1, j; i <= n; i = j + 1) {
55         j = n / (n / i);
56         LL temp = (n / i) % MO;
57         ans += temp * temp % MO * (getPhi(j) - getPhi(i - 1) + MO) % MO;
58         ans %= MO;
59     }
60     printf("%lld\n", (ans + MO) % MO);
61     return 0;
62 }