BZOJ3512 DZY Loves Math IV

解：这又是什么神仙毒瘤题......

我直接把后面那个phi用phi * I = id反演一波，得到个式子，然后推不动了......

实际上第一步我就大错特错了。考虑到n很小，我们有

然后计算S，我们根据欧拉函数的性质有：

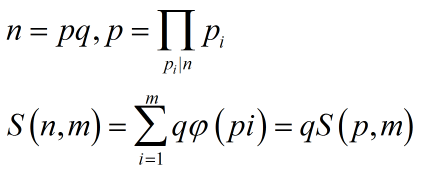
于是只考虑n sqr free的情况。

到这里有两种解法，一种是暴力递归。

考虑n的一个因子p，我们先提取出前面那一项，但是这还不够。因为当p|i的时候应该提出来p = phi[p] + 1。

于是我们在后面补上。令i = pt，就有了递归式。

  1 #include <cstdio>
  2 #include <map>
  3 
  4 typedef long long LL;
  5 const int N = 1000010, T = 1000008;
  6 const LL MO = 1e9 + 7, INF = 0x7f7f7f7f7f7f7f7fll;
  7 
  8 int phi[N], p[N], top, last[N];
  9 LL Phi[N], inv2;
 10 bool vis[N];
 11 
 12 namespace Hash {
 13     struct Node {
 14         LL val, ans;
 15         int nex;
 16         Node(LL x = 0, LL y = 0, int z = 0) {
 17             val = x;
 18             ans = y;
 19             nex = z;
 20         }
 21     }node[20000010]; int top;
 22     const int mod = 20000000;
 23     int e[mod];
 24     inline void insert(LL p, LL v) {
 25         int x = p % mod;
 26         node[++top] = Node(p, v, e[x]);
 27         e[x] = top;
 28         return;
 29     }
 30     inline LL find(LL p) {
 31         int x = p % mod;
 32         for(int i = e[x]; i; i = node[i].nex) {
 33             if(node[i].val == p) return node[i].ans;
 34         }
 35         return -INF;
 36     }
 37 }
 38 
 39 inline void getp(int n) {
 40     phi[1] = 1;
 41     for(int i = 2; i <= n; i++) {
 42         if(!vis[i]) {
 43             p[++top] = i;
 44             phi[i] = i - 1;
 45             last[i] = i;
 46         }
 47         for(int j = 1; j <= top && i * p[j] <= n; j++) {
 48             vis[i * p[j]] = 1;
 49             last[i * p[j]] = p[j];
 50             if(i % p[j] == 0) {
 51                 phi[i * p[j]] = phi[i] * p[j];
 52                 break;
 53             }
 54             phi[i * p[j]] = phi[i] * (p[j] - 1);
 55         }
 56     }
 57     for(int i = 1; i <= n; i++) {
 58         Phi[i] = (Phi[i - 1] + phi[i]) % MO;
 59     }
 60     return;
 61 }
 62 
 63 LL getPhi(LL x) {
 64     if(x <= 0) return 0;
 65     if(x <= T) return Phi[x];
 66     LL temp = Hash::find(x);
 67     if(temp != -INF) return temp;
 68     //printf("getPhi %lld T = %d\n", x, T);
 69     LL ans = (x % MO) * ((x + 1) % MO) % MO * inv2 % MO;
 70     for(LL i = 2, j; i <= x; i = j + 1) {
 71         j = x / (x / i);
 72         ans -= ((j - i + 1) % MO) * getPhi(x / i) % MO;
 73         ans = (ans % MO + MO) % MO;
 74     }
 75     Hash::insert(x, ans);
 76     return ans;
 77 }
 78 
 79 LL S(LL n, LL m) {
 80     //printf("S : %lld %lld \n", n, m);
 81     if(n == 1) return getPhi(m);
 82     if(m == 0) return 0;
 83     if(m == 1) return phi[n];
 84     LL p = last[n];
 85     LL ans = (phi[p] * S(n / p, m) % MO + S(n, m / p)) % MO;
 86     return ans;
 87 }
 88 
 89 int main() {
 90     inv2 = (MO + 1) / 2;
 91     getp(T);
 92     LL nn, m;
 93     scanf("%lld%lld", &nn, &m);
 94     LL ans = 0;
 95     for(int i = 1; i <= nn; i++) {
 96         LL p = 1, q = 1, n = i;
 97         while(n > 1) {
 98             LL temp = last[n];
 99             p *= temp;
100             n /= temp;
101             while(n % temp == 0) {
102                 n /= temp;
103                 q *= temp;
104             }
105         }
106         ans = (ans + q * S(p, m) % MO) % MO;
107     }
108     printf("%lld\n", ans);
109     return 0;
110 }

TLE

还有一种继续推：

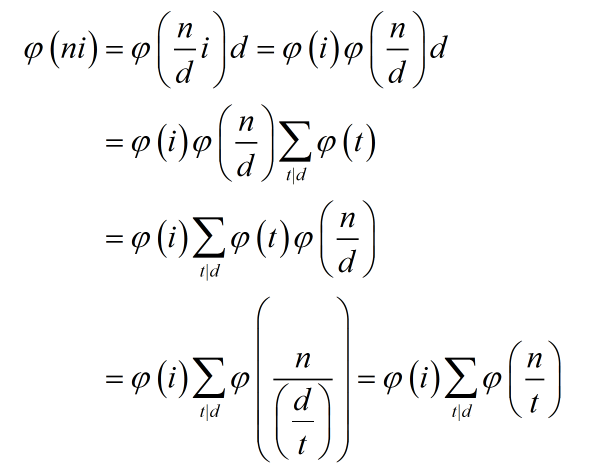
其中d = gcd(i,n)

有个关键点是n是sqr free...否则一直想不明白。

接下来把这个式子带入S的定义式中。

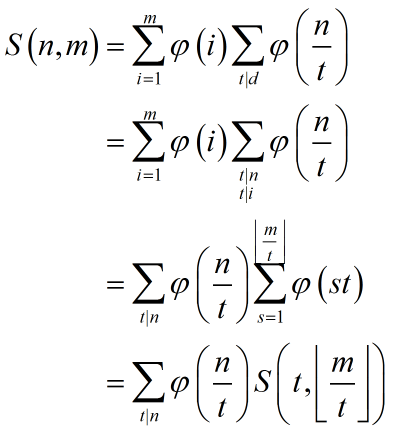
这样就可以递归了。

注意......这个S也可以记忆化的，否则死活过不去。用map。

 1 #include <cstdio>
 2 #include <map>
 3  
 4 typedef long long LL;
 5 const int N = 1000010, T = 1000008;
 6 const LL MO = 1e9 + 7, INF = 0x7f7f7f7f7f7f7f7fll;
 7  
 8 int p[N], last[N], top, phi[N];
 9 LL Phi[N], inv2;
10 bool vis[N];
11  
12 std::map<LL, LL> mp[100010], Hash;
13  
14 inline void getp(int n) {
15     phi[1] = 1;
16     for(int i = 2; i <= n; i++) {
17         if(!vis[i]) {
18             p[++top] = i;
19             phi[i] = i - 1;
20             last[i] = i;
21         }
22         for(int j = 1; j <= top && i * p[j] <= n; j++) {
23             vis[i * p[j]] = 1;
24             last[i * p[j]] = p[j];
25             if(i % p[j] == 0) {
26                 phi[i * p[j]] = phi[i] * p[j];
27                 break;
28             }
29             phi[i * p[j]] = phi[i] * (p[j] - 1);
30         }
31     }
32     for(int i = 1; i <= n; i++) {
33         Phi[i] = (Phi[i - 1] + phi[i]) % MO;
34     }
35     return;
36 }
37  
38 LL getPhi(LL x) {
39     if(x <= 0) return 0;
40     if(x <= T) return Phi[x];
41     if(Hash.count(x)) return Hash[x];
42     //printf("Phi %lld \n", x);
43     LL ans = (x % MO) * ((x + 1) % MO) % MO * inv2 % MO;
44     for(LL i = 2, j; i <= x; i = j + 1) {
45         j = x / (x / i);
46         ans -= ((j - i + 1) % MO) * getPhi(x / i) % MO;
47         ans = (ans % MO + MO) % MO;
48     }
49     return Hash[x] = ans;
50 }
51  
52 LL S(int n, LL m) {
53     //printf("S %d %lld \n", n, m);
54     if(n == 1) return getPhi(m);
55     if(m == 1) return phi[n];
56     if(m == 0) return 0;
57     if(mp[n][m]) return mp[n][m];
58     LL ans = 0;
59     for(int i = 1; i * i <= n; i++) {
60         if(n % i) continue;
61         ans += phi[n / i] * S(i, m / i) % MO;
62         if(i * i < n) {
63             ans += phi[i] * S(n / i, m / (n / i)) % MO;
64         }
65         ans = (ans % MO + MO) % MO;
66     }
67     return mp[n][m] = ans;
68 }
69  
70 int main() {
71     inv2 = (MO + 1) / 2;
72     int nn; LL m;
73     getp(T);
74     scanf("%d%lld", &nn, &m);
75     LL ans = 0;
76     for(int i = 1; i <= nn; i++) {
77         int n = i, p = 1, q = 1;
78         //printf("i = %d \n", i);
79         while(n > 1) {
80             int temp = last[n];
81             n /= temp;
82             p *= temp;
83             while(n % temp == 0) {
84                 n /= temp;
85                 q *= temp;
86             }
87         }
88         ans += q * S(p, m) % MO;
89         ans = (ans % MO + MO) % MO;
90     }
91     printf("%lld\n", ans);
92     return 0;
93 }