套路

主要放一些常见的套路。

线段树/ST表/树剖/二进制/前后缀优化连边。

树剖优化连边就是对每个重链开链长个节点，表示前缀连边。这样就可以logn做到链上连边。

线段树区间取模/与/或/开根。

就是直接打标记。主要是复杂度分析。

断环成链。

之后可以枚举端点的开始状态或者复制两倍长。

根号数据分治/时间(操作)分治。

求两个集合之间的信息时，按照集合大小根号分块。

给区间排序

可以按照左右端点，长度，中点。

区间DP

可以增加一维表示在左边加上某些东西。可以用0/1表示成为能够合并到l - 1/r + 1位置状态的代价。

数颜色相关

在几个之中出现可以等价于有多少种颜色。

序列上可以考虑莫队/two points(后缀数组常用)。子树里就建虚树，每个节点求出应该给该颜色减多少。自底向上统计。

位运算

看到位运算就想到拆位。随意异或线性基，只能异或一次就是01trie。

点边转化

构造/随机一个解之后调整。

(树上的)二维限制可以转化为平面上的区间。

树链的交/并集。

可以转化为DFS序，对应到平面上的矩形。或者按DFS序排序，减去lca的贡献。

DP

可以按照连续段DP/按照大小顺序加入DP(波浪)，关于基准点DP(要求必须经过(恰)一次该点的方案)，不断减去会算重的转移以保证前缀正确性。

一个计数trick

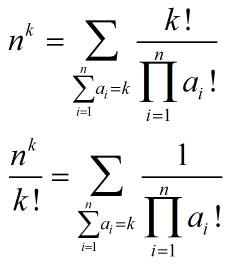
上式的意义是在大小为n的无限重集中选出k排列。故要求下式右边时可以用下式左边。

生成树权值考虑矩阵树定理和prufer序列(每个点出现次数为度数 - 1)。

小实数大量相乘的时候可以取对数转成相加。

遇到绝对值，要么就按照大小来消去，要么就所有情况暴力取最值。

遇到两棵树，距离相关问题的时候，考虑边分治 + 虚树。

计算所有1~n的权值和的时候，可以计算所有 > i的情况数。这样一个方案被计算次数恰好是它的贡献。

莫比乌斯反演：

遇到两个求和符号的时候可以尝试交换它们的顺序。

式子中有gcd的时候可以尝试枚举一个数作为gcd。

式子中有[x = 1]的时候可以尝试用∑_i|xμ(i)来替换。(μ * 1 = ι)

当存在两维限制，我们枚举其中一维的时候，第二维可能有一些非常好的性质能够快速维护更新，而不用每次再求一次。

线性基删除元素可以找到有该元素参与的所有位置，然后把最小的那个往别的所有异或。注意这个时候一定要有0这个位置。