bzoj4842 Delight for a Cat

题意：n天内你每天可以s或者e，分别有一定的收益。

每连续k天中s的天数要大于ds，e的天数要大于de，求最大收益。

解：费用流解线性规划。

先假设全部选e，然后一天s的收益为si - ei

ai表示第i天是否s，up = k - de, down = ds, R = up - down，有：

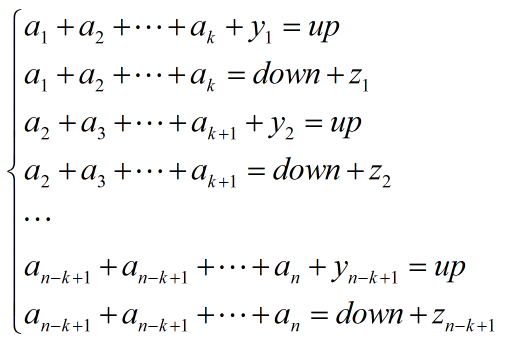
两两做差：

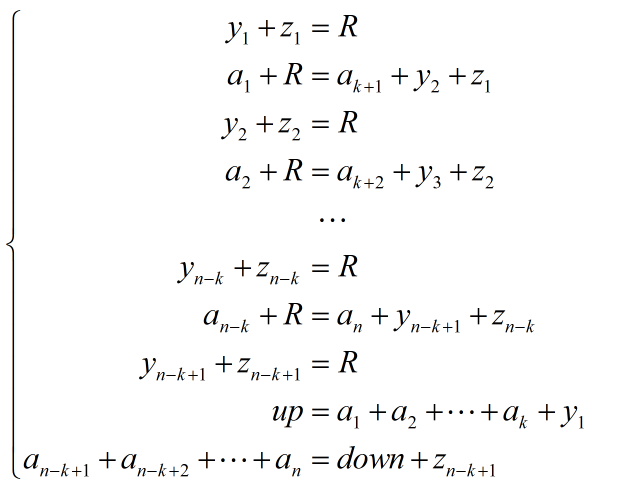
最后两个式子是人为补全的，这样就满足：每个变量在等号左边和右边各出现一次。

把每个等号看做点，每个值看做一条边。

常数项就连向源汇。

y和z代表的边啥都不需要限制，a要限流为1，费用为si - ei，然后求最大费用最大流即可。

输出方案：看改变量代表的边是否有流量即可。

  1 #include <cstdio>
  2 #include <algorithm>
  3 #include <queue>
  4 #include <cstring>
  5 
  6 typedef long long LL;
  7 const int N = 5050, M = 1000010;
  8 const LL INF = 0x3f3f3f3f3f3f3f3f;
  9 
 10 struct Edge {
 11     int nex, v;
 12     LL c, len;
 13 }edge[M << 1]; int top = 1;
 14 
 15 int e[N], vis[N], pre[N];
 16 LL d[N], flow[N];
 17 std::queue<int> Q;
 18 LL vs[N], ve[N];
 19 
 20 inline void add(int x, int y, LL z, LL w) {
 21     top++;
 22     edge[top].v = y;
 23     edge[top].c = z;
 24     edge[top].len = w;
 25     edge[top].nex = e[x];
 26     e[x] = top;
 27 
 28     top++;
 29     edge[top].v = x;
 30     edge[top].c = 0;
 31     edge[top].len = -w;
 32     edge[top].nex = e[y];
 33     e[y] = top;
 34     return;
 35 }
 36 
 37 inline bool SPFA(int s, int t) {
 38     memset(d, 0x3f, sizeof(d));
 39     d[s] = 0;
 40     flow[s] = INF;
 41     vis[s] = 1;
 42     Q.push(s);
 43     while(!Q.empty()) {
 44         int x = Q.front();
 45         Q.pop();
 46         vis[x] = 0;
 47         for(int i = e[x]; i; i = edge[i].nex) {
 48             int y = edge[i].v;
 49             if(edge[i].c && d[y] > d[x] + edge[i].len) {
 50                 d[y] = d[x] + edge[i].len;
 51                 pre[y] = i;
 52                 flow[y] = std::min(flow[x], edge[i].c);
 53                 if(!vis[y]) {
 54                     vis[y] = 1;
 55                     Q.push(y);
 56                 }
 57             }
 58         }
 59     }
 60     return d[t] < INF;
 61 }
 62 
 63 inline void update(int s, int t) {
 64     LL temp = flow[t];
 65     while(t != s) {
 66         int i = pre[t];
 67         edge[i].c -= temp;
 68         edge[i ^ 1].c += temp;
 69         t = edge[i ^ 1].v;
 70     }
 71     return;
 72 }
 73 
 74 inline LL solve(int s, int t, LL &cost) {
 75     LL ans = 0;
 76     cost = 0;
 77     while(SPFA(s, t)) {
 78         ans += flow[t];
 79         cost += flow[t] * d[t];
 80         update(s, t);
 81     }
 82     return ans;
 83 }
 84 
 85 int main() {
 86     int n, k, ds, de;
 87     LL sum = 0;
 88     scanf("%d%d%d%d", &n, &k, &ds, &de);
 89     for(int i = 1; i <= n; i++) {
 90         scanf("%lld", &vs[i]);
 91     }
 92     for(int i = 1; i <= n; i++) {
 93         scanf("%lld", &ve[i]);
 94         sum += ve[i];
 95         vs[i] -= ve[i];
 96     }
 97     int up = k - de,  down = ds, lm = n - k + 1;
 98     int s = N - 1, t = N - 2;
 99     for(int i = 1; i <= n - k + 1; i++) {
100         if(i == 1) { // yi
101             add(i, lm * 2 + 1, INF, 0ll);
102         }
103         else {
104             add(i, lm + i - 1, INF, 0ll);
105         }
106         if(i == n - k + 1) { // zi
107             add(i, lm * 2 + 2, INF, 0ll);
108         }
109         else {
110             add(i, lm + i, INF, 0ll);
111         }
112     }
113     int OP = top;
114     for(int i = 1; i <= n; i++) {
115         // ai
116         int ss = lm + i, tt = i - k + lm;
117         if(i <= k) {
118             tt = lm * 2 + 1;
119         }
120         if(i >= n - k + 1) {
121             ss = lm * 2 + 2;
122         }
123         add(ss, tt, 1ll, -vs[i]);
124     }
125     int ED = top;
126     for(int i = 1; i <= n - k + 1; i++) {
127         add(s, i, up - down, 0ll);
128         add(i + lm, t, up - down, 0ll);
129     }
130     add(lm * 2 + 1, t, up, 0ll);
131     add(s, lm * 2 + 2, down, 0ll);
132 
133     LL ans;
134     solve(s, t, ans);
135     printf("%lld\n", sum - ans);
136     for(int i = OP + 1; i <= ED; i += 2) {
137         if(edge[i].c) {
138             putchar('E');
139         }
140         else {
141             putchar('S');
142         }
143     }
144     return 0;
145 }