网络流24题 gay题报告

洛谷上面有一整套题。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 extra

①飞行员配对方案问题。top

裸二分图匹配。

 1 #include <cstdio>
 2 
 3 const int N = 110, M = 10010;
 4 
 5 struct Edge {
 6     int nex, v;
 7 }edge[M << 1]; int top;
 8 
 9 int n, m, e[N], mat[N], vis[N], Time;
10 
11 inline void add(int x, int y) {
12     top++;
13     edge[top].v = y;
14     edge[top].nex = e[x];
15     e[x] = top;
16     return;
17 }
18 
19 bool DFS(int x) {
20     for(int i = e[x]; i; i = edge[i].nex) {
21         int y = edge[i].v;
22         if(vis[y] == Time) {
23             continue;
24         }
25         vis[y] = Time;
26         if(!mat[y] || DFS(mat[y])) {
27             mat[y] = x;
28             return 1;
29         }
30     }
31     return 0;
32 }
33 
34 int main() {
35     scanf("%d%d", &m, &n);
36     int x, y;
37     while(scanf("%d%d", &x, &y)) {
38         if(x == -1 && y == -1) {
39             break;
40         }
41         add(x, y);
42         add(y, x);
43     }
44 
45     int ans = 0;
46     for(int i = 1; i <= m; i++) {
47         Time = i;
48         if(DFS(i)) {
49             ans++;
50         }
51     }
52 
53     if(!ans) {
54         printf("No Solution!");
55         return 0;
56     }
57 
58     printf("%d\n", ans);
59     for(int i = m + 1; i <= n; i++) {
60         if(mat[i]) {
61             printf("%d %d", mat[i], i);
62             ans--;
63             if(ans) {
64                 puts("");
65             }
66         }
67     }
68 
69     return 0;
70 }

匈牙利AC代码

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int N = 10010, M = 100010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N];
 13 std::queue<int> Q;
 14 
 15 inline void add(int x, int y, int z) {
 16     top++;
 17     edge[top].nex = e[x];
 18     edge[top].v = y;
 19     edge[top].c = z;
 20     e[x] = top;
 21     return;
 22 }
 23 
 24 inline bool BFS(int s, int t) {
 25     memset(d, 0x3f, sizeof(d));
 26     d[s] = 1;
 27     Q.push(s);
 28     while(!Q.empty()) {
 29         int x = Q.front();
 30         Q.pop();
 31         for(int i = e[x]; i; i = edge[i].nex) {
 32             int y = edge[i].v;
 33             if(edge[i].c && d[y] == INF) {
 34                 d[y] = d[x] + 1;
 35                 Q.push(y);
 36             }
 37         }
 38     }
 39     return d[t] < INF;
 40 }
 41 
 42 int DFS(int x, int t, int maxF) {
 43     if(x == t) {
 44         return maxF;
 45     }
 46     int ans = 0;
 47     for(int i = e[x]; i; i = edge[i].nex) {
 48         int y = edge[i].v;
 49         if(d[x] + 1 != d[y] || !edge[i].c) {
 50             continue;
 51         }
 52         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 53         if(!temp) {
 54             d[y] = 0;
 55         }
 56         ans += temp;
 57         edge[i].c -= temp;
 58         edge[i ^ 1].c += temp;
 59         if(ans == maxF) {
 60             return ans;
 61         }
 62     }
 63     return ans;
 64 }
 65 
 66 int solve(int s, int t) {
 67     int ans = 0;
 68     while(BFS(s, t)) {
 69         ans += DFS(s, t, INF);
 70     }
 71     return ans;
 72 }
 73 
 74 int main() {
 75     int n, m;
 76     scanf("%d%d", &m, &n);
 77     int x, y;
 78     while(scanf("%d%d", &x, &y)) {
 79         if(x == -1) {
 80             break;
 81         }
 82         add(x, y, 1);
 83         add(y, x, 0);
 84         //printf("%d %d \n", x, y);
 85     }
 86     int s = n + 1, t = n + 2;
 87     for(int i = 1; i <= m; i++) {
 88         add(s, i, 1);
 89         add(i, s, 0);
 90         //printf("s %d \n", i);
 91     }
 92     for(int i = m + 1; i <= n; i++) {
 93         add(i, t, 1);
 94         add(t, i, 0);
 95         //printf("%d t \n", i);
 96     }
 97 
 98     int ans = solve(s, t);
 99     if(!ans) {
100         printf("No Solution!");
101         return 0;
102     }
103     printf("%d\n", ans);
104     for(int i = 2; i <= top; i += 2) {
105         if(edge[i].c || edge[i ^ 1].v == s || edge[i].v == t) {
106             continue;
107         }
108         printf("%d %d", edge[i ^ 1].v, edge[i].v);
109         ans--;
110         if(ans) {
111             puts("");
112         }
113     }
114 
115     return 0;
116 }

DinicAC代码

②负载平衡问题。top

环形均分纸牌。也可以用费用流做。

首先每个人的牌数是sum/n，这点可以建立源汇，用流量来控制。

所以代价交换次数最小就用费用来控制。

相邻之间连边，费用为1，流量INF。

每个点与源连边，流量为一开始的牌数，费用为0。

每个点与汇连边，流量为sum/n，费用为0。

然后跑最小费用最大流。

(这里注意，无向边费用流，对于一条边要建4条边才行。

最大流可以只建两条边，流量都为c，但是费用流的费用要取负，不好搞。)

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int N = 210, M = 50010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c, len;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], pre[N], Time, flow[N];
 13 std::queue<int> Q;
 14 bool vis[M];
 15 
 16 inline void add(int x, int y, int z, int w) {
 17     top++;
 18     edge[top].nex = e[x];
 19     edge[top].v = y;
 20     edge[top].c = z;
 21     edge[top].len = w;
 22     e[x] = top;
 23     top++;
 24     edge[top].v = x;
 25     edge[top].c = 0;
 26     edge[top].len = -w;
 27     edge[top].nex = e[y];
 28     e[y] = top;
 29     return;
 30 }
 31 
 32 inline bool SPFA(int s, int t) {
 33     memset(d, 0x3f, sizeof(d));
 34     d[s] = 0;
 35     vis[s] = Time;
 36     flow[s] = INF;
 37     Q.push(s);
 38     while(!Q.empty()) {
 39         int x = Q.front();
 40         Q.pop();
 41         vis[x] = 0;
 42         for(int i = e[x]; i; i = edge[i].nex) {
 43             int y = edge[i].v;
 44             if(!edge[i].c) {
 45                 continue;
 46             }
 47             if(d[y] > d[x] + edge[i].len) {
 48                 d[y] = d[x] + edge[i].len;
 49                 pre[y] = i;
 50                 flow[y] = std::min(flow[x], edge[i].c);
 51                 //printf("y = %d d = %d flow = %d \n", y, d[y], flow[y]);
 52                 if(vis[y] != Time) {
 53                     vis[y] = Time;
 54                     Q.push(y);
 55                 }
 56             }
 57         }
 58     }
 59     /*for(int i = 1; i <= 7; i++) {
 60         printf("%d %d \n", d[i], flow[i]);
 61     }*/
 62     return d[t] < INF; // error 0
 63 }
 64 
 65 inline void update(int s, int t) {
 66     int f = flow[t], i = pre[t];
 67     while(t != s) {
 68         edge[i].c -= f;
 69         edge[i ^ 1].c += f;
 70         t = edge[i ^ 1].v;
 71         i = pre[t];
 72     }
 73     return;
 74 }
 75 
 76 int solve(int s, int t, int &cost) {
 77     int ans = 0;
 78     cost = 0;
 79     Time = 1;
 80     while(SPFA(s, t)) {
 81         ans += flow[t];
 82         cost += flow[t] * d[t];
 83         update(s, t);
 84         Time++;
 85         //printf("%d %d \n", ans, cost);
 86     }
 87     return ans;
 88 }
 89 
 90 int main() {
 91     int n, sum = 0;
 92     scanf("%d", &n);
 93     int s = n + 1, t = n + 2;
 94     for(int i = 1, x; i <= n; i++) {
 95         scanf("%d", &x);
 96         sum += x;
 97         if(i > 1) {
 98             add(i, i - 1, INF, 1);
 99         }
100         if(i < n) {
101             add(i, i + 1, INF, 1);
102         }
103         add(s, i, x, 0);
104     }
105     add(1, n, INF, 1);
106     add(n, 1, INF, 1);
107     sum /= n;
108     for(int i = 1; i <= n; i++) {
109         add(i, t, sum, 0);
110     }
111 
112     int ans, cost;
113     ans = solve(s, t, cost);
114     printf("%d", cost);
115     return 0;
116 }

AC代码

③软件补丁问题。top

٩(๑>◡<๑)۶

这题看了一会，想到一个状压+SPFA转移的做法，算一下复杂度好像不行，但是没有别的算法了....

跑去看题解，还真是？？！！

弃疗了。

④魔术球问题。top

这题，我有个非常SB的二分费用流！

然后果断T掉......

没事，我会动态加点！然后加出负环来了...GG。

负环如下：

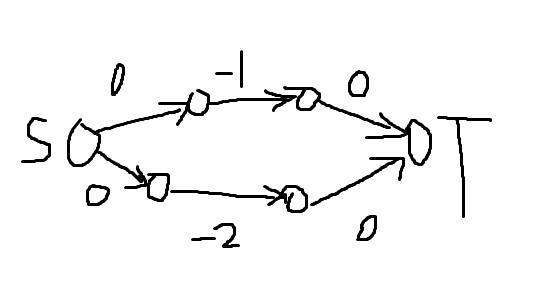
图中所有流量为1，数字表示费用。先加上面三条边，然后跑一遍，然后加下面三条边再跑。

可以发现此时出现了流量为1的负环.......

然后跑去看题解，嗯？？？最小路径覆盖？(我傻了。)

然后根据题解的启示，回想小凯的疑惑，用找规律A了......

讲一下我的SB费用流。

我们发现点数不好一开始确定，进而想到二分。

然后如何判定呢？

首先建图，如果和为完全平方数，就小->大连边。

源汇往每个点连边。

这样的话，可以用一条流量表示一个柱子，源点限流n，球限流1。但是发现一个问题：每个点都有一条路径为源->该点->汇。这样不是没有意义了吗？

不！我们可以求最大费用啊！那么就可以让你经过尽量多的球了。

所以每个球内部的那条边，费用为负编号。别的费用都为0。

观察最大费用是否为∑i即可。

输出方案就是先搜索源点的出边，找到满流的为起点。

然后枚举每一条边，把每个节点的后继找到。然后就可以输出了。

正确的做法：发现其实就是最小路径覆盖......;

还是二分，然后看最小路径覆盖是不是等于n。

(还有人用搜索过...)

  1 #include <cstdio>
  2 #include <algorithm>
  3 #include <cstring>
  4 #include <queue>
  5 
  6 const int N = 10010, M = 1000019, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c, len;
 10 }edge[M << 1]; int top;
 11 
 12 int e[N], d[N], pre[N], flow[N], vis[N], Time, n, ss;
 13 std::queue<int> Q;
 14 bool sqr[N];
 15 
 16 inline void add(int x, int y, int z, int w) {
 17     top++;
 18     edge[top].v = y;
 19     edge[top].c = z;
 20     edge[top].len = w;
 21     edge[top].nex = e[x];
 22     e[x] = top;
 23 
 24     top++;
 25     edge[top].v = x;
 26     edge[top].c = 0;
 27     edge[top].len = -w;
 28     edge[top].nex = e[y];
 29     e[y] = top;
 30     return;
 31 }
 32 
 33 inline bool SPFA(int s, int t) {
 34     memset(d, 0x3f, sizeof(d));
 35     d[s] = 0;
 36     vis[s] = Time;
 37     flow[s] = INF;
 38     Q.push(s);
 39     while(!Q.empty()) {
 40         int x = Q.front();
 41         Q.pop();
 42         vis[x] = 0;
 43         for(int i = e[x]; i; i = edge[i].nex) {
 44             int y = edge[i].v;
 45             if(edge[i].c && d[y] > d[x] + edge[i].len) {
 46                 d[y] = d[x] + edge[i].len;
 47                 flow[y] = std::min(flow[x], edge[i].c);
 48                 pre[y] = i;
 49                 if(vis[y] != Time) {
 50                     vis[y] = Time;
 51                     Q.push(y);
 52                 }
 53             }
 54         }
 55     }
 56     return d[t] < INF;
 57 }
 58 
 59 inline void update(int s, int t) {
 60     int f = flow[t];
 61     int i = pre[t];
 62     while(s != t) {
 63         edge[i].c -= f;
 64         edge[i ^ 1].c += f;
 65         t = edge[i ^ 1].v;
 66         i = pre[t];
 67     }
 68     return;
 69 }
 70 
 71 inline int solve(int s, int t, int &cost) {
 72     int ans = 0;
 73     cost = 0;
 74     Time = 1;
 75     memset(vis, 0, sizeof(vis));
 76     while(SPFA(s, t)) {
 77         ans += flow[t];
 78         cost += flow[t] * d[t];
 79         update(s, t);
 80         Time++;
 81     }
 82     return ans;
 83 }
 84 
 85 inline bool check(int k) {
 86     //printf("k = %d \n", k);
 87     memset(e, 0, sizeof(e));
 88     top = 1;
 89     int s = k + k + 1, t = k + k + 2;
 90     ss = k + k + 3;
 91     add(s, ss, n, 0);
 92     for(int i = 1; i <= k; i++) {
 93         add(i, i + k, 1, -i);
 94         add(ss, i, 1, 0);
 95         add(i + k, t, 1, 0);
 96     }
 97     for(int i = 1; i < k; i++) {
 98         for(int j = i + 1; j <= k; j++) {
 99             if(sqr[i + j]) {
100                 add(i + k, j, 1, 0);
101             }
102         }
103     }
104     int cost;
105     solve(s, t, cost);
106     //printf("max cost = %d \n", -cost);
107     return cost + (k + 1) * k / 2 == 0;
108 }
109 
110 int main() {
111     for(int i = 1; i <= 100; i++) {
112         sqr[i * i] = 1;
113     }
114     scanf("%d", &n);
115     int l = n, r = 1567;
116     if(l > 10) {
117         l <<= 1;
118     }
119     while(l < r) {
120         int mid = (l + r + 1) >> 1;
121         if(check(mid)) {
122             l = mid;
123         }
124         else {
125             r = mid - 1;
126         }
127     }
128     check(r);
129     printf("%d\n", r);
130     std::priority_queue<int, std::vector<int>, std::greater<int> > P;
131     for(int i = e[ss]; i; i = edge[i].nex) {
132         int y = edge[i].v;
133         if(!edge[i].c) {
134             P.push(y);
135         }
136     }
137     memset(pre, 0, sizeof(pre));
138     for(int i = 2; i <= top; i += 2) {
139         int y = edge[i].v;
140         int x = edge[i ^ 1].v;
141         if(!edge[i].c && r < x && x <= r * 2 && y <= r && x - r < y) {
142             pre[x - r] = y;
143 
144         }
145     }
146 
147     while(!P.empty()) {
148         int x = P.top();
149         P.pop();
150         while(x) {
151             printf("%d ", x);
152             x = pre[x];
153         }
154         puts("");
155     }
156 
157     return 0;
158 }

费用流二分TLE

  1 #include <cstdio>
  2 #include <algorithm>
  3 #include <cstring>
  4 #include <queue>
  5 
  6 const int N = 10010, M = 1000019, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c, len;
 10 }edge[M << 1]; int top;
 11 
 12 int e[N], d[N], pre[N], flow[N], vis[N], Time, n, ss;
 13 std::queue<int> Q;
 14 bool sqr[N];
 15 
 16 inline void add(int x, int y, int z, int w) {
 17     top++;
 18     edge[top].v = y;
 19     edge[top].c = z;
 20     edge[top].len = w;
 21     edge[top].nex = e[x];
 22     e[x] = top;
 23 
 24     top++;
 25     edge[top].v = x;
 26     edge[top].c = 0;
 27     edge[top].len = -w;
 28     edge[top].nex = e[y];
 29     e[y] = top;
 30     return;
 31 }
 32 
 33 inline bool SPFA(int s, int t) {
 34     memset(d, 0x3f, sizeof(d));
 35     d[s] = 0;
 36     vis[s] = Time;
 37     flow[s] = INF;
 38     Q.push(s);
 39     while(!Q.empty()) {
 40         int x = Q.front();
 41         Q.pop();
 42         vis[x] = 0;
 43         for(int i = e[x]; i; i = edge[i].nex) {
 44             int y = edge[i].v;
 45             if(edge[i].c && d[y] > d[x] + edge[i].len) {
 46                 d[y] = d[x] + edge[i].len;
 47                 flow[y] = std::min(flow[x], edge[i].c);
 48                 pre[y] = i;
 49                 if(vis[y] != Time) {
 50                     vis[y] = Time;
 51                     Q.push(y);
 52                 }
 53             }
 54         }
 55     }
 56     return d[t] < INF;
 57 }
 58 
 59 inline void update(int s, int t) {
 60     int f = flow[t];
 61     int i = pre[t];
 62     while(s != t) {
 63         edge[i].c -= f;
 64         edge[i ^ 1].c += f;
 65         t = edge[i ^ 1].v;
 66         i = pre[t];
 67     }
 68     return;
 69 }
 70 
 71 inline int solve(int s, int t, int &cost) {
 72     int ans = 0;
 73     cost = 0;
 74     Time = 1;
 75     memset(vis, 0, sizeof(vis));
 76     while(SPFA(s, t)) {
 77         ans += flow[t];
 78         cost += flow[t] * d[t];
 79         update(s, t);
 80         Time++;
 81     }
 82     return ans;
 83 }
 84 
 85 inline bool check(int k) {
 86     //printf("k = %d \n", k);
 87     memset(e, 0, sizeof(e));
 88     top = 1;
 89     int s = k + k + 1, t = k + k + 2;
 90     ss = k + k + 3;
 91     add(s, ss, n, 0);
 92     for(int i = 1; i <= k; i++) {
 93         add(i, i + k, 1, -i);
 94         add(ss, i, 1, 0);
 95         add(i + k, t, 1, 0);
 96     }
 97     for(int i = 1; i < k; i++) {
 98         for(int j = i + 1; j <= k; j++) {
 99             if(sqr[i + j]) {
100                 add(i + k, j, 1, 0);
101             }
102         }
103     }
104     int cost;
105     solve(s, t, cost);
106     //printf("max cost = %d \n", -cost);
107     return cost + (k + 1) * k / 2 == 0;
108 }
109 
110 int main() {
111     for(int i = 1; i <= 100; i++) {
112         sqr[i * i] = 1;
113     }
114     scanf("%d", &n);
115     int r;
116     if((n & 1) == 0) {
117         r = n * (n / 2 + 1) - 1;
118     }
119     else {
120         r = (n + 1) * (n + 1) / 2 - 1;
121     }
122     check(r);
123     printf("%d\n", r);
124     std::priority_queue<int, std::vector<int>, std::greater<int> > P;
125     for(int i = e[ss]; i; i = edge[i].nex) {
126         int y = edge[i].v;
127         if(!edge[i].c) {
128             P.push(y);
129         }
130     }
131     memset(pre, 0, sizeof(pre));
132     for(int i = 2; i <= top; i += 2) {
133         int y = edge[i].v;
134         int x = edge[i ^ 1].v;
135         if(!edge[i].c && r < x && x <= r * 2 && y <= r && x - r < y) {
136             pre[x - r] = y;
137 
138         }
139     }
140 
141     while(!P.empty()) {
142         int x = P.top();
143         P.pop();
144         while(x) {
145             printf("%d ", x);
146             x = pre[x];
147         }
148         puts("");
149     }
150 
151     return 0;
152 }

费用流AC代码

⑤孤岛营救问题。top

sjf天天在那说什么拯救大兵瑞恩，有心理阴影了，告辞。

最后还是写了......

因为之前的某个契机，一直在想枚举拿哪个钥匙。

后来思路陡然开阔，反正边权都为1，不就是状压BFS吗???

然后想着写个主程序就走，写了一半发现好像比较好写，就把读入和预处理也写了，然后就完美的避开了所有坑一A了...

  1 #include <queue>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int INF = 0x3f3f3f3f, N = 20;
  7 const int dx[] = {0, 0, 1, -1};
  8 const int dy[] = {1, -1, 0, 0};
  9 
 10 struct Node {
 11     int x, y, s;
 12     Node(int X, int Y, int S) {
 13         x = X;
 14         y = Y;
 15         s = S;
 16     }
 17 };
 18 
 19 int G[N][N], d[N][N][1030], line[N][N], row[N][N], vis[N][N][1030];
 20 std::queue<Node> Q;
 21 int n, m, p;
 22 
 23 inline bool valid(int x, int y, int s, int i) {
 24     if(i < 2) { // row
 25         y = std::min(y, y + dy[i]);
 26         if(row[x][y] == -1)  {
 27             return 0;
 28         }
 29         return (s | row[x][y]) == s;
 30     }
 31     else { // line
 32         x = std::min(x, x + dx[i]);
 33         if(line[x][y] == -1) {
 34             return 0;
 35         }
 36         return (s | line[x][y]) == s;
 37     }
 38 }
 39 
 40 inline void BFS() {
 41     memset(d, 0x3f, sizeof(d));
 42     d[1][1][G[1][1]] = 0;
 43     vis[1][1][G[1][1]] = 1;
 44     Q.push(Node(1, 1, G[1][1]));
 45     while(!Q.empty()) {
 46         int x = Q.front().x;
 47         int y = Q.front().y;
 48         int s = Q.front().s;
 49         Q.pop();
 50         for(int i = 0; i < 4; i++) {
 51             if(!valid(x, y, s, i)) {
 52                 continue;
 53             }
 54             int tx = x + dx[i];
 55             int ty = y + dy[i];
 56             int ts = s | G[tx][ty];
 57             if(vis[tx][ty][ts]) {
 58                 continue;
 59             }
 60             d[tx][ty][ts] = d[x][y][s] + 1;
 61             vis[tx][ty][ts] = 1;
 62             Q.push(Node(tx, ty, ts));
 63         }
 64     }
 65 
 66     return;
 67 }
 68 
 69 int main() {
 70     scanf("%d%d%d", &n, &m, &p);
 71     int k, A, B, C, D, E;
 72     scanf("%d", &k);
 73     for(int i = 1; i <= k; i++) {
 74         scanf("%d%d%d%d%d", &A, &B, &C, &D, &E);
 75         if(A > C) {
 76             std::swap(A, C);
 77             std::swap(B, D);
 78         }
 79         if(B > D) {
 80             std::swap(A, C);
 81             std::swap(B, D);
 82         }
 83         if(A == C) {
 84             row[A][B] = E ? (1 << (E - 1)) : -1;
 85         }
 86         else if(B == D) {
 87             line[A][B] = E ? (1 << (E - 1)) : -1;
 88         }
 89     }
 90     int s;
 91     scanf("%d", &s);
 92     for(int i = 1; i <= s; i++) {
 93         scanf("%d%d%d", &A, &B, &E);
 94         G[A][B] |= (1 << (E - 1));
 95     }
 96     for(int i = 1; i <= n; i++) {
 97         row[i][0] = row[i][m] = -1;
 98     }
 99     for(int i = 1; i <= m; i++) {
100         line[0][i] = line[n][i] = -1;
101     }
102     BFS();
103     int ans = INF;
104     for(int i = 0; i < (1 << p); i++) {
105         ans = std::min(ans, d[n][m][i]);
106     }
107     if(ans == INF) {
108         ans = -1;
109     }
110     printf("%d", ans);
111     return 0;
112 }

AC代码

⑥圆桌问题。top

本人多次将m, n打错...

每张桌子上每组人不能超过1个。

通过限制流量为1来实现。

源点向组连流量为人数的边，桌子向汇点连流量为可容纳人数的边。

桌子和组之间两两连流量为1的边。

如果最大流小于总人数，就不合法。

方案就是每组的满流出边代表的桌子。

  1 #include <cstdio>
  2 #include <algorithm>
  3 #include <queue>
  4 #include <cstring>
  5 // #define id(i, j) (((i) - 1) * m + (j))
  6 
  7 const int N = 1010, M = 200010, INF = 0x3f3f3f3f;
  8 
  9 struct Edge {
 10     int nex, v, c;
 11 }edge[M << 1]; int top = 1;
 12 
 13 int e[N], d[N];
 14 std::queue<int> Q;
 15 
 16 inline void add(int x, int y, int z) {
 17     //printf("add : %d %d \n", x, y);
 18 
 19     top++;
 20     edge[top].v = y;
 21     edge[top].c = z;
 22     edge[top].nex = e[x];
 23     e[x] = top;
 24 
 25     top++;
 26     edge[top].v = x;
 27     edge[top].c = 0;
 28     edge[top].nex = e[y];
 29     e[y] = top;
 30     return;
 31 }
 32 
 33 inline bool BFS(int s, int t) {
 34     memset(d, 0, sizeof(d));
 35     d[s] = 1;
 36     Q.push(s);
 37     while(!Q.empty()) {
 38         int x = Q.front();
 39         Q.pop();
 40         for(int i = e[x]; i; i = edge[i].nex) {
 41             int y = edge[i].v;
 42             if(!edge[i].c || d[y]) {
 43                 continue;
 44             }
 45             d[y] = d[x] + 1;
 46             Q.push(y);
 47         }
 48     }
 49     return d[t];
 50 }
 51 
 52 int DFS(int x, int t, int maxF) {
 53     if(x == t) {
 54         return maxF;
 55     }
 56     int ans = 0;
 57     for(int i = e[x]; i; i = edge[i].nex) {
 58         int y = edge[i].v;
 59         if(!edge[i].c || d[x] + 1 != d[y]) {
 60             continue;
 61         }
 62         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 63         if(!temp) {
 64             d[y] = 0;
 65         }
 66         ans += temp;
 67         edge[i].c -= temp;
 68         edge[i ^ 1].c += temp;
 69         if(ans == maxF) {
 70             break;
 71         }
 72     }
 73     return ans;
 74 }
 75 
 76 inline int solve(int s, int t) {
 77     int ans = 0;
 78     while(BFS(s, t)) {
 79         ans += DFS(s, t, INF);
 80     }
 81     return ans;
 82 }
 83 
 84 int main() {
 85     int n, m, sum = 0;
 86     scanf("%d%d", &m, &n);
 87     int s = n + m + 1, t = n + m + 2;
 88     for(int i = 1, x; i <= m; i++) {
 89         scanf("%d", &x);
 90         add(s, i, x);
 91         sum += x;
 92     }
 93     for(int i = 1, x; i <= n; i++) {
 94         scanf("%d", &x);
 95         add(m + i, t, x);
 96         for(int j = 1; j <= m; j++) {
 97             add(j, m + i, 1);
 98         }
 99     }
100 
101     if(solve(s, t) != sum) {
102         puts("0");
103         return 0;
104     }
105     puts("1");
106 
107     for(int x = 1; x <= m; x++) {
108         for(int i = e[x]; i; i = edge[i].nex) {
109             int y = edge[i].v;
110             if(edge[i].c || y == s) {
111                 continue;
112             }
113             printf("%d ", y - m);
114         }
115         puts("");
116     }
117 
118     return 0;
119 }

AC代码

⑦汽车加油行驶问题。top

这TM是最短路啊......

我一开始发现比较复杂，然后想着用费用流，只给一个流量，然后发现这不就是最短路吗...

具体来说，因为只能走k步比较难处理，就一次性把这k步全走了好了......

关于强制消费：看这个样例。

7 5 4 5 100
0 0 0 0 0 0 0
0 0 0 0 0 0 0
1 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 1 1 1 1 0 0

嗯，可以发现最优路线要在最底下进行绕路......

这启示我们用BFS来连边。

然后就被这个神逻辑题给烦死了......

看代码了。

  1 #include <cstdio>
  2 #include <queue>
  3 #include <algorithm>
  4 #include <cstring>
  5 
  6 const int N = 20010, M = 2000010, INF = 0x3f3f3f3f;
  7 const int dx[] = {0, 1, 0, -1};
  8 const int dy[] = {1, 0, -1, 0};
  9 
 10 struct Edge {
 11     int nex, v, len;
 12 }edge[M << 1]; int top;
 13 
 14 struct Node {
 15     int x, d;
 16     Node(int X, int D) {
 17         x = X;
 18         d = D;
 19     }
 20     inline bool operator <(const Node &w) const {
 21         return d > w.d;
 22     }
 23 };
 24 
 25 struct POI {
 26     int x, y, d, dist;
 27     POI(int X, int Y, int D, int T) {
 28         x = X;
 29         y = Y;
 30         d = D;
 31         dist = T;
 32     }
 33 };
 34 
 35 int e[N], dis[N], vis[N], n, B, G[105][105], use[105][105];
 36 std::priority_queue<Node> Q;
 37 std::queue<POI> P;
 38 
 39 inline void add(int x, int y, int z) {
 40     top++;
 41     edge[top].v = y;
 42     edge[top].len = z;
 43     edge[top].nex = e[x];
 44     e[x] = top;
 45     return;
 46 }
 47 
 48 inline void dijkstra(int s) {
 49     memset(dis, 0x3f, sizeof(dis));
 50     dis[s] = 0;
 51     Q.push(Node(s, 0));
 52     while(!Q.empty()) {
 53         int x = Q.top().x;
 54         if(vis[x] || dis[x] != Q.top().d) {
 55             Q.pop();
 56             continue;
 57         }
 58         Q.pop();
 59         vis[x] = 1;
 60         for(int i = e[x]; i; i = edge[i].nex) {
 61             int y = edge[i].v;
 62             if(!vis[y] && dis[y] > dis[x] + edge[i].len) {
 63                 dis[y] = dis[x] + edge[i].len;
 64                 /*if(y == 21) {
 65                     printf("x = %d  y = %d  d[y] = %d \n", x, y, dis[y]);
 66                 }*/
 67                 Q.push(Node(y, dis[y]));
 68             }
 69         }
 70     }
 71     return;
 72 }
 73 
 74 inline int cal(int i, int j, int a, int b) {
 75     //printf("cal : (%d %d) -> (%d %d)  %d \n", i, j, a, b, B * (std::max(0, i - a) + std::max(0, j - b)));
 76     /*if(i == 1 && j == 2 && a == 1 && b == 1) {
 77         printf("fds ans = %d \n", B * (std::max(0, i - a) + std::max(0, j - b)));
 78     }*/
 79     return B * (std::max(0, i - a) + std::max(0, j - b));
 80 }
 81 
 82 inline int id(int x, int y) {
 83     return (x - 1) * n + y;
 84 }
 85 
 86 int main() {
 87     int K, A, c;
 88     scanf("%d%d%d%d%d", &n, &K, &A, &B, &c);
 89     int lm = n * n;
 90     for(int i = 1; i <= n; i++) {
 91         for(int j = 1; j <= n; j++) {
 92             scanf("%d", &use[i][j]);
 93         }
 94     }
 95     for(int i = 1; i <= n; i++) {
 96         for(int j = 1, f; j <= n; j++) {
 97             int T = id(i, j);
 98             add(T, T + lm, use[i][j] ? A : A + c);
 99             G[i][j] = T;
100             P.push(POI(i, j, 1, 0));
101             while(!P.empty()) {
102                 int x = P.front().x;
103                 int y = P.front().y;
104                 int d = P.front().d;
105                 int dist = P.front().dist;
106                 P.pop();
107                 for(int k = 0; k < 4; k++) {
108                     int tx = x + dx[k];
109                     int ty = y + dy[k];
110                     if(tx && ty && tx <= n && ty <= n && G[tx][ty] != T) {
111                         add(T + lm, id(tx, ty), dist + ((k > 1) ? B : 0));
112                         G[tx][ty] = T;
113                         //printf("%d %d  = %d %d   d = %d \n", i, j, tx, ty, d);
114                         if(d < K && !use[tx][ty]) {
115                             P.push(POI(tx, ty, d + 1, dist + ((k > 1) ? B : 0)));
116                         }
117                     }
118                 }
119             }
120         }
121     }
122 
123     dijkstra(id(1, 1) + lm);
124 
125     printf("%d", dis[id(n, n)]);
126     /*int x, y;
127     while(scanf("%d%d", &x, &y)) {
128         printf("%d \n", dis[id(x, y)]);
129     }*/
130     return 0;
131 }

AC代码

⑧分配问题。top

源点向人连边，人和工作之间n²连边，工作向汇点连边。

最大/小费用最大流。

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int N = 210, M = 20010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c, len;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], pre[N], Time, flow[N], G[N][N];
 13 std::queue<int> Q;
 14 bool vis[M];
 15 
 16 inline void add(int x, int y, int z, int w) {
 17     top++;
 18     edge[top].nex = e[x];
 19     edge[top].v = y;
 20     edge[top].c = z;
 21     edge[top].len = w;
 22     e[x] = top;
 23     top++;
 24     edge[top].v = x;
 25     edge[top].c = 0;
 26     edge[top].len = -w;
 27     edge[top].nex = e[y];
 28     e[y] = top;
 29     return;
 30 }
 31 
 32 inline bool SPFA(int s, int t) {
 33     memset(d, 0x3f, sizeof(d));
 34     d[s] = 0;
 35     vis[s] = Time;
 36     flow[s] = INF;
 37     Q.push(s);
 38     while(!Q.empty()) {
 39         int x = Q.front();
 40         Q.pop();
 41         vis[x] = 0;
 42         for(int i = e[x]; i; i = edge[i].nex) {
 43             int y = edge[i].v;
 44             if(!edge[i].c) {
 45                 continue;
 46             }
 47             if(d[y] > d[x] + edge[i].len) {
 48                 d[y] = d[x] + edge[i].len;
 49                 pre[y] = i;
 50                 flow[y] = std::min(flow[x], edge[i].c);
 51                 if(vis[y] != Time) {
 52                     vis[y] = Time;
 53                     Q.push(y);
 54                 }
 55             }
 56         }
 57     }
 58     return d[t] < INF; // error 0
 59 }
 60 
 61 inline void update(int s, int t) {
 62     int f = flow[t], i = pre[t];
 63     while(t != s) {
 64         edge[i].c -= f;
 65         edge[i ^ 1].c += f;
 66         t = edge[i ^ 1].v;
 67         i = pre[t];
 68     }
 69     return;
 70 }
 71 
 72 int solve(int s, int t, int &cost) {
 73     int ans = 0;
 74     cost = 0;
 75     Time = 1;
 76     while(SPFA(s, t)) {
 77         ans += flow[t];
 78         cost += flow[t] * d[t];
 79         update(s, t);
 80         Time++;
 81     }
 82     return ans;
 83 }
 84 
 85 int main() {
 86     int n;
 87     scanf("%d", &n);
 88     int s = n << 1 | 1, t = (n + 1) << 1;
 89     for(int i = 1; i <= n; i++) {
 90         for(int j = 1; j <= n; j++) {
 91             int x;
 92             scanf("%d", &G[i][j]);
 93             add(i, n + j, 1, G[i][j]);
 94         }
 95         add(s, i, 1, 0);
 96         add(n + i, t, 1, 0);
 97     }
 98 
 99     int cost;
100     solve(s, t, cost);
101     printf("%d\n", cost);
102 
103     memset(vis, 0, sizeof(vis));
104     int temp = 1;
105     for(int i = 1; i <= n; i++) {
106         for(int j = 1; j <= n; j++) {
107             edge[++temp].c = 1;
108             edge[temp].len = -G[i][j];
109             edge[++temp].c = 0;
110             edge[temp].len = G[i][j];
111         }
112         edge[++temp].c = 1;
113         edge[++temp].c = 0;
114         edge[++temp].c = 1;
115         edge[++temp].c = 0;
116     }
117 
118     solve(s, t, cost);
119     printf("%d", -cost);
120 
121     return 0;
122 }

AC代码

⑨试题库问题。top

每个种类建点，每个试题建点。

源点向种类连流量为需求量的边，试题向汇点连流量为1的边。

试题和能匹配的种类之间连流量为1的边。

然后跑最大流。如果小于总需求量就无解。

方案就是每个种类出去的满流的边。

有个坑：当某一种类需求量为0的时候我的写法会输出源点。解决办法是不加那一条边。

  1 #include <cstdio>
  2 #include <algorithm>
  3 #include <queue>
  4 #include <cstring>
  5 // #define id(i, j) (((i) - 1) * m + (j))
  6 
  7 const int N = 10010, M = 200010, INF = 0x3f3f3f3f;
  8 
  9 struct Edge {
 10     int nex, v, c;
 11 }edge[M << 1]; int top = 1;
 12 
 13 int e[N], d[N], G[100][100];
 14 std::queue<int> Q;
 15 
 16 inline void add(int x, int y, int z) {
 17     top++;
 18     edge[top].v = y;
 19     edge[top].c = z;
 20     edge[top].nex = e[x];
 21     e[x] = top;
 22 
 23     top++;
 24     edge[top].v = x;
 25     edge[top].c = 0;
 26     edge[top].nex = e[y];
 27     e[y] = top;
 28     return;
 29 }
 30 
 31 inline bool BFS(int s, int t) {
 32     memset(d, 0, sizeof(d));
 33     d[s] = 1;
 34     Q.push(s);
 35     while(!Q.empty()) {
 36         int x = Q.front();
 37         Q.pop();
 38         for(int i = e[x]; i; i = edge[i].nex) {
 39             int y = edge[i].v;
 40             if(!edge[i].c || d[y]) {
 41                 continue;
 42             }
 43             d[y] = d[x] + 1;
 44             Q.push(y);
 45         }
 46     }
 47     return d[t];
 48 }
 49 
 50 int DFS(int x, int t, int maxF) {
 51     if(x == t) {
 52         return maxF;
 53     }
 54     int ans = 0;
 55     for(int i = e[x]; i; i = edge[i].nex) {
 56         int y = edge[i].v;
 57         if(!edge[i].c || d[x] + 1 != d[y]) {
 58             continue;
 59         }
 60         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 61         if(!temp) {
 62             d[y] = 0;
 63         }
 64         ans += temp;
 65         edge[i].c -= temp;
 66         edge[i ^ 1].c += temp;
 67         if(ans == maxF) {
 68             break;
 69         }
 70     }
 71     return ans;
 72 }
 73 
 74 inline int solve(int s, int t) {
 75     int ans = 0;
 76     while(BFS(s, t)) {
 77         ans += DFS(s, t, INF);
 78     }
 79     return ans;
 80 }
 81 
 82 int main() {
 83     int n, k, sum = 0;
 84     scanf("%d%d", &k, &n);
 85     int s = n + k + 1, t = n + k + 2;
 86     for(int i = 1, x; i <= k; i++) {
 87         scanf("%d", &x);
 88         if(x) {
 89             add(s, i, x);
 90         }
 91         sum += x;
 92     }
 93     for(int i = 1, x, y; i <= n; i++) {
 94         scanf("%d", &y);
 95         for(int j = 1; j <= y; j++) {
 96             scanf("%d", &x);
 97             add(x, k + i, 1);
 98         }
 99         add(k + i, t, 1);
100     }
101 
102     if(solve(s, t) != sum) {
103         printf("No Solution!");
104         return 0;
105     }
106 
107     for(int a = 1; a <= k; a++) {
108         printf("%d: ", a);
109         for(int i = e[a]; i; i = edge[i].nex) {
110             int y = edge[i].v;
111             if(edge[i].c) {
112                 continue;
113             }
114             printf("%d ", y - k);
115         }
116         puts("");
117     }
118 
119 
120     return 0;
121 }

AC代码

⑩运输问题。top

跟T8差不多吧......

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <queue>
  4 
  5 const int INF = 0x3f3f3f3f;
  6 
  7 struct EK {
  8     struct Edge {
  9         int v, nex, f, len;
 10         inline void cl() {
 11             v = nex = f = len = 0;
 12             return;
 13         }
 14     }edge[100 * 102 * 2 + 2]; int top;
 15     int e[203], dis[203], pre[203], flow[203], vis[203];
 16     EK() {
 17         top = 1;
 18     }
 19     inline void clear() {
 20         for(int i = 2; i <= top; i++) {
 21             edge[i].cl();
 22         }
 23         top = 1;
 24         memset(pre, 0, sizeof(pre));
 25         memset(dis, 0, sizeof(dis));
 26         memset(vis, 0, sizeof(vis));
 27         memset(flow, 0, sizeof(flow));
 28         memset(e, 0, sizeof(e));
 29         return;
 30     }
 31     inline void add(int x, int y, int z, int l) {
 32         top++;
 33         edge[top].v = y;
 34         edge[top].f = z;
 35         edge[top].len = l;
 36         edge[top].nex = e[x];
 37         e[x] = top++;
 38         edge[top].v = x;
 39         edge[top].f = 0;
 40         edge[top].len = -l;
 41         edge[top].nex = e[y];
 42         e[y] = top;
 43         return;
 44     }
 45     inline bool SPFA(int s, int t) {
 46         memset(dis, 0x3f, sizeof(dis));
 47         memset(vis, 0, sizeof(vis));
 48         std::queue<int> Q;
 49         Q.push(s);
 50         vis[s] = 1;
 51         dis[s] = 0;
 52         flow[s] = INF;
 53         while(!Q.empty()) {
 54             int x = Q.front();
 55             Q.pop();
 56             vis[x] = 0;
 57             for(int i = e[x]; i; i = edge[i].nex) {
 58                 int y = edge[i].v;
 59                 if(edge[i].f && dis[y] > dis[x] + edge[i].len) {
 60                     dis[y] = dis[x] + edge[i].len;
 61                     pre[y] = i;
 62                     flow[y] = std::min(flow[x], edge[i].f);
 63                     if(vis[y]) {
 64                         continue;
 65                     }
 66                     vis[y] = 1;
 67                     Q.push(y);
 68                 }
 69             }
 70         }
 71         return dis[t] < INF;
 72     }
 73     inline void update(int s, int t) {
 74         int p = t;
 75         while(p != s) {
 76             int i = pre[p];
 77             edge[i].f -= flow[t];
 78             edge[i ^ 1].f += flow[t];
 79             p = edge[i ^ 1].v;
 80         }
 81         return;
 82     }
 83     inline void solve(int s, int t, int &maxF, int &cost) {
 84         maxF = cost = 0;
 85         while(SPFA(s, t)) {
 86             maxF += flow[t];
 87             cost += flow[t] * dis[t];
 88             //printf("%d %d\n", flow[t], dis[t]);
 89             update(s, t);
 90         }
 91         return;
 92     }
 93 }ek;
 94 
 95 int G[101][101], a[101], b[101];
 96 
 97 int main() {
 98     int m, n;
 99     scanf("%d%d", &n, &m);
100     for(int i = 1; i <= n; i++) {
101         scanf("%d", &a[i]);
102     }
103     for(int i = 1; i <= m; i++) {
104         scanf("%d", &b[i]);
105     }
106     for(int i = 1; i <= n; i++) {
107         for(int j = 1; j <= m; j++) {
108             scanf("%d", &G[i][j]);
109         }
110     }
111 
112     int S = n + m + 1, T = n + m + 2;
113 
114     for(int i = 1; i <= n; i++) {
115         ek.add(S, i, a[i], 0);
116     }
117     for(int i = 1; i <= m; i++) {
118         ek.add(n + i, T, b[i], 0);
119     }
120     for(int i = 1; i <= n; i++) {
121         for(int j = 1; j <= m; j++) {
122             ek.add(i, n + j, INF, G[i][j]);
123         }
124     }
125 
126     int c, d;
127     ek.solve(S, T, c, d);
128     printf("%d\n", d);
129 
130     ek.clear();
131     for(int i = 1; i <= n; i++) {
132         ek.add(S, i, a[i], 0);
133     }
134     for(int i = 1; i <= m; i++) {
135         ek.add(n + i, T, b[i], 0);
136     }
137     for(int i = 1; i <= n; i++) {
138         for(int j = 1; j <= m; j++) {
139             ek.add(i, n + j, INF, -G[i][j]);
140         }
141     }
142 
143     ek.solve(S, T, c, d);
144     printf("%d", -d);
145 
146     return 0;
147 }

AC代码

①①太空飞行计划问题。top

另写了篇博客。

①②最小路径覆盖问题。top

模板题....

DAG最小路径覆盖数 = n - 转二分图后最大流

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int N = 1010, M = 100010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], vis[N], nex[N];
 13 std::queue<int> Q;
 14 
 15 inline void add(int x, int y, int z) {
 16     top++;
 17     edge[top].v = y;
 18     edge[top].c = z;
 19     edge[top].nex = e[x];
 20     e[x] = top;
 21 
 22     top++;
 23     edge[top].v = x;
 24     edge[top].c = 0;
 25     edge[top].nex = e[y];
 26     e[y] = top;
 27     return;
 28 }
 29 
 30 inline bool BFS(int s, int t) {
 31     memset(d, 0, sizeof(d));
 32     d[s] = 1;
 33     Q.push(s);
 34     while(!Q.empty()) {
 35         int x = Q.front();
 36         Q.pop();
 37         for(int i = e[x]; i; i = edge[i].nex) {
 38             int y = edge[i].v;
 39             if(!edge[i].c || d[y]) {
 40                 continue;
 41             }
 42             d[y] = d[x] + 1;
 43             Q.push(y);
 44         }
 45     }
 46     return d[t];
 47 }
 48 
 49 int DFS(int x, int t, int maxF) {
 50     if(x == t) {
 51         return maxF;
 52     }
 53     int ans = 0;
 54     for(int i = e[x]; i; i = edge[i].nex) {
 55         int y = edge[i].v;
 56         if(!edge[i].c || d[x] + 1 != d[y]) {
 57             continue;
 58         }
 59         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 60         if(!temp) {
 61             d[y] = 0;
 62         }
 63         ans += temp;
 64         edge[i].c -= temp;
 65         edge[i ^ 1].c += temp;
 66         if(ans == maxF) {
 67             break;
 68         }
 69     }
 70     return ans;
 71 }
 72 
 73 inline int solve(int s, int t) {
 74     int ans = 0;
 75     while(BFS(s, t)) {
 76         ans += DFS(s, t, INF);
 77         //printf("ans = %d \n", ans);
 78     }
 79     return ans;
 80 }
 81 
 82 int main() {
 83     int n, m;
 84     scanf("%d%d", &n, &m);
 85     for(int i = 1, x, y; i <= m; i++) {
 86         scanf("%d%d", &x, &y);
 87         add(x, y + n, 1);
 88     }
 89     int s = n + n + 1, t = n + n + 2;
 90     for(int i = 1; i <= n; i++) {
 91         add(s, i, 1);
 92         add(n + i, t, 1);
 93     }
 94 
 95     int ans = solve(s, t);
 96     memset(vis, -1, sizeof(vis));
 97     for(int i = 2; i <= (m << 1); i += 2) {
 98         if(edge[i].c) {
 99             continue;
100         }
101         //printf("chose  %d -> %d \n", edge[i ^ 1].v, edge[i].v - n);
102         nex[edge[i ^ 1].v] = edge[i].v - n;
103         vis[edge[i].v - n] = 0;
104     }
105 
106     for(int i = 1; i <= n; i++) {
107         if(vis[i]) {
108             int x = i;
109             while(x) {
110                 printf("%d ", x);
111                 x = nex[x];
112             }
113             puts("");
114         }
115     }
116 
117     printf("%d", n - ans);
118     return 0;
119 }

AC代码

①③方格取数问题。top

二分图带权最大独立集 -> 二分图带权最小点覆盖。

做法是给每个点它的权值大小的流量，两部之间的流量为INF。

然后取最大流就是带权最小点覆盖。

可以感性理解一下：对于每一条边，两边一定有一个点满流，表示选择该点。严谨的证明不会...

  1 #include <cstdio>
  2 #include <algorithm>
  3 #include <queue>
  4 #include <cstring>
  5 #define id(i, j) (((i) - 1) * m + (j))
  6 
  7 const int N = 10010, M = 200010, INF = 0x3f3f3f3f;
  8 
  9 struct Edge {
 10     int nex, v, c;
 11 }edge[M << 1]; int top = 1;
 12 
 13 int e[N], d[N], G[100][100];
 14 std::queue<int> Q;
 15 
 16 inline void add(int x, int y, int z) {
 17     top++;
 18     edge[top].v = y;
 19     edge[top].c = z;
 20     edge[top].nex = e[x];
 21     e[x] = top;
 22 
 23     top++;
 24     edge[top].v = x;
 25     edge[top].c = 0;
 26     edge[top].nex = e[y];
 27     e[y] = top;
 28     return;
 29 }
 30 
 31 inline bool BFS(int s, int t) {
 32     memset(d, 0, sizeof(d));
 33     d[s] = 1;
 34     Q.push(s);
 35     while(!Q.empty()) {
 36         int x = Q.front();
 37         Q.pop();
 38         for(int i = e[x]; i; i = edge[i].nex) {
 39             int y = edge[i].v;
 40             if(!edge[i].c || d[y]) {
 41                 continue;
 42             }
 43             d[y] = d[x] + 1;
 44             Q.push(y);
 45         }
 46     }
 47     return d[t];
 48 }
 49 
 50 int DFS(int x, int t, int maxF) {
 51     if(x == t) {
 52         return maxF;
 53     }
 54     int ans = 0;
 55     for(int i = e[x]; i; i = edge[i].nex) {
 56         int y = edge[i].v;
 57         if(!edge[i].c || d[x] + 1 != d[y]) {
 58             continue;
 59         }
 60         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 61         if(!temp) {
 62             d[y] = 0;
 63         }
 64         ans += temp;
 65         edge[i].c -= temp;
 66         edge[i ^ 1].c += temp;
 67         if(ans == maxF) {
 68             break;
 69         }
 70     }
 71     return ans;
 72 }
 73 
 74 inline int solve(int s, int t) {
 75     int ans = 0;
 76     while(BFS(s, t)) {
 77         ans += DFS(s, t, INF);
 78     }
 79     return ans;
 80 }
 81 
 82 int main() {
 83     int n, m, sum = 0;
 84     scanf("%d%d", &n, &m);
 85     int s = n * m + 1, t = n * m + 2;
 86     for(int i = 1; i <= n; i++) {
 87         for(int j = 1; j <= m; j++) {
 88             scanf("%d", &G[i][j]);
 89             sum += G[i][j];
 90             if((i + j) & 1) {
 91                 add(s, id(i, j), G[i][j]);
 92             }
 93             else {
 94                 add(id(i, j), t, G[i][j]);
 95             }
 96         }
 97     }
 98     for(int i = 1; i <= n; i++) {
 99         for(int j = 1; j <= m; j++) {
100             if(i < n) { // |
101                 if((i + j) & 1) {
102                     add(id(i, j), id(i + 1, j), INF);
103                 }
104                 else {
105                     add(id(i + 1, j), id(i, j), INF);
106                 }
107             }
108             if(j < m) { // --
109                 if((i + j) & 1) {
110                     add(id(i, j), id(i, j + 1), INF);
111                 }
112                 else {
113                     add(id(i, j + 1), id(i, j), INF);
114                 }
115             }
116         }
117     }
118 
119     printf("%d", sum - solve(s, t));
120 
121     return 0;
122 }

AC代码

①④最长k可重区间集问题。top

毒瘤...跟下面的17是一样的...17有个要注意的地方。

一开始受到下面15的启发，准备限制每个流的长度为k，发现不好控制最长。

一直在想怎么竖着流，期间想到过横着流但是没有深究...

两种建图方式，这里和17各自讲一种。

由于一个位置最多只能有k个区间，我们不妨把答案分成k层，用k个流量来模拟每一层。

有的位置不到k个怎么办？连额外的边引流。

具体来说，对于每两个彻底分离的区间，都连费用为0，流量为1的边表示它们可能在同一层。

每个区间内部限流为1，费用为自己的长度。

然后从起点流出k个流量，向每个区间连边表示它可能是起点。

每个区间向汇点连边表示它可能是终点。

大概长这样......

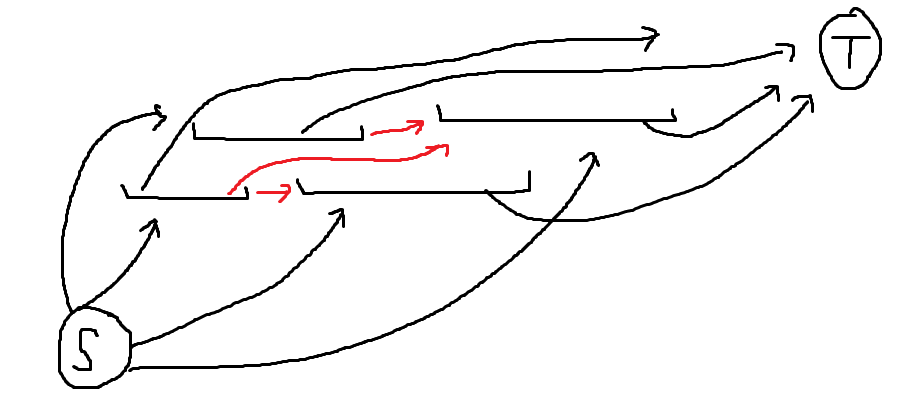
额外连一条s->t的边表示不到k个(不连也不会出问题)。

跑最大费用最大流即可。

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int N = 5010, M = 50010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c, len;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], pre[N], Time, flow[N], l[N], r[N];
 13 std::queue<int> Q;
 14 bool vis[M];
 15 
 16 inline void add(int x, int y, int z, int w) {
 17     top++;
 18     edge[top].nex = e[x];
 19     edge[top].v = y;
 20     edge[top].c = z;
 21     edge[top].len = w;
 22     e[x] = top;
 23     top++;
 24     edge[top].v = x;
 25     edge[top].c = 0;
 26     edge[top].len = -w;
 27     edge[top].nex = e[y];
 28     e[y] = top;
 29     return;
 30 }
 31 
 32 inline bool SPFA(int s, int t) {
 33     memset(d, 0x3f, sizeof(d));
 34     d[s] = 0;
 35     vis[s] = Time;
 36     flow[s] = INF;
 37     Q.push(s);
 38     while(!Q.empty()) {
 39         int x = Q.front();
 40         Q.pop();
 41         vis[x] = 0;
 42         for(int i = e[x]; i; i = edge[i].nex) {
 43             int y = edge[i].v;
 44             if(!edge[i].c) {
 45                 continue;
 46             }
 47             if(d[y] > d[x] + edge[i].len) {
 48                 d[y] = d[x] + edge[i].len;
 49                 pre[y] = i;
 50                 flow[y] = std::min(flow[x], edge[i].c);
 51                 if(vis[y] != Time) {
 52                     vis[y] = Time;
 53                     Q.push(y);
 54                 }
 55             }
 56         }
 57     }
 58     return d[t] < INF; // error 0
 59 }
 60 
 61 inline void update(int s, int t) {
 62     int f = flow[t], i = pre[t];
 63     //printf("update : ");
 64     while(t != s) {
 65         //printf("%d ", t);
 66         edge[i].c -= f;
 67         edge[i ^ 1].c += f;
 68         t = edge[i ^ 1].v;
 69         i = pre[t];
 70     }
 71     //puts("");
 72     return;
 73 }
 74 
 75 int solve(int s, int t, int &cost) {
 76     int ans = 0;
 77     cost = 0;
 78     Time = 1;
 79     while(SPFA(s, t)) {
 80         ans += flow[t];
 81         cost += flow[t] * d[t];
 82         update(s, t);
 83         Time++;
 84     }
 85     return ans;
 86 }
 87 
 88 int main() {
 89     int n, k;
 90     scanf("%d%d", &n, &k);
 91     for(int i = 1; i <= n; i++) {
 92         scanf("%d%d", &l[i], &r[i]);
 93     }
 94 
 95     int s = n * 2 + 1, t = n * 2 + 2, ss = n * 2 + 3;
 96     for(int i = 1; i <= n; i++) {
 97         for(int j = 1; j <= n; j++) {
 98             if(r[i] <= l[j]) {
 99                 add(i + n, j, 1, 0);
100                 //printf("add : %d %d \n", i, j);
101             }
102         }
103         add(i, i + n, 1, l[i] - r[i]);
104         add(s, i, 1, 0);
105         add(i + n, t, 1, 0);
106     }
107     add(ss, s, k, 0);
108     add(s, t, INF, 0);
109     int cost;
110     solve(ss, t, cost);
111     printf("%d", -cost);
112 
113     return 0;
114 }

AC代码

①⑤最长不下降子序列问题。top

又是个毒瘤...首先第一问可以很轻易的用n² DP求出来，答案为s。

然后考虑我们要限制每条流量的长度为s，这搞鬼...？？

问了红太阳，他说把每个点拆成s个，然后每一层只向下一层连边。

然后跑最大流。不会出现一个点在不同的层数被使用多次的情况，因为i号点只能是序列中的第f[i]个，也就是f[i]层。

然后我们发现一个问题：这样建图会有500002个点，GG......

注意前面发现的一个东西：每个点只有在f[i]层有用，这样就可以把别的层都给去掉，点数缩减到了n。可过。

具体建图:

如果i < j && a[i] <= a[j] && f[i] + 1 == f[j]

连流量为1的边。

每个点限流为1。

源汇分别向f[i] == 1和f[i] == s连边，流量为1。

然后最大流就是第二问。

关于第三问：1和n可以用无限次。

要提到一个坑点就是要找的必须是下标不同的。所以样例不能一直取35，1 1也不能一直取1。

特判掉s == 1然后把1，n的限流改为INF，如果有源->1(一定有)就改为INF，如果有n->汇同理。

然后再来一次最大流。

注意：我的方法是把每条边的流量都重置，其实可以直接在残余网络上加边，跑出来的答案累加。

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <algorithm>
  4 #include <queue>
  5 
  6 const int N = 2010, M = 3000010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], a[509], f[509], ans, n;
 13 std::queue<int> Q;
 14 
 15 inline void add(int x, int y, int z) {
 16     top++;
 17     edge[top].v = y;
 18     edge[top].c = z;
 19     edge[top].nex = e[x];
 20     e[x] = top;
 21     top++;
 22     edge[top].v = x;
 23     edge[top].c = 0;
 24     edge[top].nex = e[y];
 25     e[y] = top;
 26     return;
 27 }
 28 
 29 inline bool BFS(int s, int t) {
 30     memset(d, 0, sizeof(d));
 31     d[s] = 1;
 32     Q.push(s);
 33     while(!Q.empty()) {
 34         int x = Q.front();
 35         Q.pop();
 36         for(int i = e[x]; i; i = edge[i].nex) {
 37             int y = edge[i].v;
 38             if(!edge[i].c || d[y]) {
 39                 continue;
 40             }
 41             d[y] = d[x] + 1;
 42             Q.push(y);
 43         }
 44     }
 45     return d[t];
 46 }
 47 
 48 int DFS(int x, int t, int maxF) {
 49     //printf("x = %d maxF = %d \n", x, maxF);
 50     if(x == t) {
 51         return maxF;
 52     }
 53     int ans = 0;
 54     for(int i = e[x]; i; i = edge[i].nex) {
 55         int y = edge[i].v;
 56         if(!edge[i].c || d[x] + 1 != d[y]) {
 57             continue;
 58         }
 59         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 60         if(!temp) {
 61             d[y] = 0;
 62         }
 63         ans += temp;
 64         edge[i].c -= temp;
 65         edge[i ^ 1].c += temp;
 66         if(ans == maxF) {
 67             break;
 68         }
 69     }
 70     return ans;
 71 }
 72 
 73 inline int solve(int s, int t) {
 74     int ans = 0;
 75     while(BFS(s, t)) {
 76         ans += DFS(s, t, INF);
 77     }
 78     return ans;
 79 }
 80 
 81 int main() {
 82 
 83     scanf("%d", &n);
 84     for(int i = 1; i <= n; i++) {
 85         scanf("%d", &a[i]);
 86     }
 87     for(int i = 1; i <= n; i++) {
 88         for(int j = 1; j < i; j++) {
 89             if(a[i] >= a[j]) {
 90                 f[i] = std::max(f[i], f[j]);
 91             }
 92         }
 93         f[i]++;
 94         ans = std::max(ans, f[i]);
 95     }
 96     printf("%d\n", ans);
 97 
 98     int s = n << 1 | 1;
 99     int t = s + 1;
100 
101     for(int i = 1; i <= n; i++) {
102         for(int j = i + 1; j <= n; j++) {
103             if(a[i] <= a[j] && f[i] + 1 == f[j]) {
104                 add(i + n, j, 1);
105             }
106         }
107         add(i, i + n, 1);
108         if(f[i] == 1) {
109             add(s, i, 1);
110         }
111         if(f[i] == ans) {
112             add(i + n, t, 1);
113         }
114     }
115 
116     printf("%d\n", solve(s, t));
117 
118     if(ans == 1) {
119         printf("%d", n);
120         return 0;
121     }
122 
123     int temp = 1;
124     for(int i = 1; i <= n; i++) {
125         for(int j = i + 1; j <= n; j++) {
126             if(a[i] <= a[j] && f[i] + 1 == f[j]) {
127                 edge[++temp].c = 1;
128                 edge[++temp].c = 0;
129             }
130         }
131         bool flag = (i == 1 || i == n);
132         edge[++temp].c = flag ? INF : 1;
133         edge[++temp].c = 0;
134         if(f[i] == 1) {
135             edge[++temp].c = flag ? INF : 1;
136             edge[++temp].c = 0;
137         }
138         if(f[i] == ans) {
139             edge[++temp].c = flag ? INF : 1;
140             edge[++temp].c = 0;
141         }
142     }
143 
144     printf("%d", solve(s, t));
145     return 0;
146 }

AC代码重置流量

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <algorithm>
  4 #include <queue>
  5 
  6 const int N = 2010, M = 3000010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], a[509], f[509], ans, n;
 13 std::queue<int> Q;
 14 
 15 inline void add(int x, int y, int z) {
 16     top++;
 17     edge[top].v = y;
 18     edge[top].c = z;
 19     edge[top].nex = e[x];
 20     e[x] = top;
 21     top++;
 22     edge[top].v = x;
 23     edge[top].c = 0;
 24     edge[top].nex = e[y];
 25     e[y] = top;
 26     return;
 27 }
 28 
 29 inline bool BFS(int s, int t) {
 30     memset(d, 0, sizeof(d));
 31     d[s] = 1;
 32     Q.push(s);
 33     while(!Q.empty()) {
 34         int x = Q.front();
 35         Q.pop();
 36         for(int i = e[x]; i; i = edge[i].nex) {
 37             int y = edge[i].v;
 38             if(!edge[i].c || d[y]) {
 39                 continue;
 40             }
 41             d[y] = d[x] + 1;
 42             Q.push(y);
 43         }
 44     }
 45     return d[t];
 46 }
 47 
 48 int DFS(int x, int t, int maxF) {
 49     //printf("x = %d maxF = %d \n", x, maxF);
 50     if(x == t) {
 51         return maxF;
 52     }
 53     int ans = 0;
 54     for(int i = e[x]; i; i = edge[i].nex) {
 55         int y = edge[i].v;
 56         if(!edge[i].c || d[x] + 1 != d[y]) {
 57             continue;
 58         }
 59         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 60         if(!temp) {
 61             d[y] = 0;
 62         }
 63         ans += temp;
 64         edge[i].c -= temp;
 65         edge[i ^ 1].c += temp;
 66         if(ans == maxF) {
 67             break;
 68         }
 69     }
 70     return ans;
 71 }
 72 
 73 inline int solve(int s, int t) {
 74     int ans = 0;
 75     while(BFS(s, t)) {
 76         ans += DFS(s, t, INF);
 77     }
 78     return ans;
 79 }
 80 
 81 int main() {
 82 
 83     //freopen("in.in", "r", stdin);
 84     //freopen("my.out", "w", stdout);
 85 
 86     scanf("%d", &n);
 87     for(int i = 1; i <= n; i++) {
 88         scanf("%d", &a[i]);
 89     }
 90     for(int i = 1; i <= n; i++) {
 91         for(int j = 1; j < i; j++) {
 92             if(a[i] >= a[j]) {
 93                 f[i] = std::max(f[i], f[j]);
 94             }
 95         }
 96         f[i]++;
 97         ans = std::max(ans, f[i]);
 98     }
 99     printf("%d\n", ans);
100 
101     int s = n << 1 | 1;
102     int t = s + 1;
103 
104     for(int i = 1; i <= n; i++) {
105         for(int j = i + 1; j <= n; j++) {
106             if(a[i] <= a[j] && f[i] + 1 == f[j]) {
107                 add(i + n, j, 1);
108             }
109         }
110         add(i, i + n, 1);
111         if(f[i] == 1) {
112             add(s, i, 1);
113         }
114         if(f[i] == ans) {
115             add(i + n, t, 1);
116         }
117     }
118     int r = solve(s, t);
119     printf("%d\n", r);
120 
121     if(ans == 1) {
122         printf("%d", n);
123         return 0;
124     }
125     add(s, 1, INF);
126     add(1, n + 1, INF);
127     add(n, n + n ,INF);
128     if(f[n] == ans) {
129         add(n + n, t, INF);
130     }
131 
132     printf("%d", solve(s, t) + r);
133     return 0;
134 }

AC代码残余网络

①⑥骑士共存问题。top

首先想到行列连边，然后发现是马，就二分图了。

最大独立集 = n - 最大匹配。

有个坑点就是划分集合的时候，不能按照编号的奇偶性，例如2 * 2的棋盘，就是14一组，23一组。

要按照行+列的奇偶性。

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <algorithm>
  4 #include <queue>
  5 
  6 const int N = 40010, M = 1000010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], n, m, G[210][210];
 13 std::queue<int> Q;
 14 
 15 inline void add(int x, int y, int z) {
 16     top++;
 17     edge[top].v = y;
 18     edge[top].c = z;
 19     edge[top].nex = e[x];
 20     e[x] = top;
 21     top++;
 22     edge[top].v = x;
 23     edge[top].c = 0;
 24     edge[top].nex = e[y];
 25     e[y] = top;
 26     return;
 27 }
 28 
 29 inline bool BFS(int s, int t) {
 30     memset(d, 0, sizeof(d));
 31     d[s] = 1;
 32     Q.push(s);
 33     while(!Q.empty()) {
 34         int x = Q.front();
 35         Q.pop();
 36         for(int i = e[x]; i; i = edge[i].nex) {
 37             int y = edge[i].v;
 38             if(!edge[i].c || d[y]) {
 39                 continue;
 40             }
 41             d[y] = d[x] + 1;
 42             Q.push(y);
 43         }
 44     }
 45     return d[t];
 46 }
 47 
 48 int DFS(int x, int t, int maxF) {
 49     if(x == t) {
 50         return maxF;
 51     }
 52     int ans = 0;
 53     for(int i = e[x]; i; i = edge[i].nex) {
 54         int y = edge[i].v;
 55         if(!edge[i].c || d[x] + 1 != d[y]) {
 56             continue;
 57         }
 58         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 59         if(!temp) {
 60             d[y] = 0;
 61         }
 62         edge[i].c -= temp;
 63         edge[i ^ 1].c += temp;
 64         ans += temp;
 65         if(ans == maxF) {
 66             break;
 67         }
 68     }
 69     return ans;
 70 }
 71 
 72 inline int solve(int s, int t) {
 73     int ans = 0;
 74     while(BFS(s, t)) {
 75         ans += DFS(s, t, INF);
 76     }
 77     return ans;
 78 }
 79 
 80 inline int id(int x, int y) {
 81     return (x - 1) * n + y;
 82 }
 83 
 84 int main() {
 85     int x, y;
 86     scanf("%d%d", &n, &m);
 87     for(int i = 1; i <= m; i++) {
 88         scanf("%d%d", &x, &y);
 89         G[x][y] = 1;
 90     }
 91     int s = n * n + 1, t = n * n + 2;
 92     for(int i = 1; i < n; i++) {
 93         for(int j = 1; j <= n; j++) {
 94             if(G[i][j]) {
 95                 continue;
 96             }
 97             int a = id(i, j);
 98             bool f = (i + j) & 1;
 99             if(f) {
100                 add(s, a, 1);
101             }
102             else {
103                 add(a, t, 1);
104             }
105             //printf("x = %d %d \n", i, j);
106             if(j > 2 && !G[i + 1][j - 2]) {
107                 if(f) {
108                     add(a, id(i + 1, j - 2), 1);
109                 }
110                 else {
111                     add(id(i + 1, j - 2), a, 1);
112                 }
113                 //printf("    y = %d %d \n", i + 1, j - 2);
114             }
115             if(j > 1 && i + 1 < n && !G[i + 2][j - 1]) {
116                 if(f) {
117                     add(a, id(i + 2, j - 1), 1);
118                 }
119                 else {
120                     add(id(i + 2, j - 1), a, 1);
121                 }
122                 //printf("    y = %d %d \n", i + 2, j - 1);
123             }
124             if(j + 1 < n && !G[i + 1][j + 2]) {
125                 if(f) {
126                     add(a, id(i + 1, j + 2), 1);
127                 }
128                 else {
129                     add(id(i + 1, j + 2), a, 1);
130                 }
131                 //printf("    y = %d %d \n", i + 1, j + 2);
132             }
133             if(j < n && i + 1 < n && !G[i + 2][j + 1]) {
134                 if(f) {
135                     add(a, id(i + 2, j + 1), 1);
136                 }
137                 else {
138                     add(id(i + 2, j + 1), a, 1);
139                 }
140                 //printf("    y = %d %d \n", i + 2, j - 1);
141             }
142         }
143     }
144     for(int j = 1; j <= n; j++) {
145         if(!G[n][j]) {
146             int a = id(n, j);
147             if((n + j) & 1) {
148                 add(s, a, 1);
149             }
150             else {
151                 add(a, t, 1);
152             }
153         }
154     }
155 
156     int ans = solve(s, t);
157     //printf("%d \n", ans);
158 
159     printf("%d", n * n - m - ans);
160 
161     return 0;
162 }

AC代码

①⑦最长k可重线段集问题。top

上面14的带权版本。

新的建图方式：

还是用k个流量来模拟k层，一开始他们全在x轴上面流淌(什么沙雕动词...)，费用为0。

然后如果这里可以选一个线段，就分出去一个流量，表示这里有了一个线段。

具体来说，先把横坐标离散化，同时预处理出每个线段的长度。

先把x轴串成一串。然后对于每个线段，从左端点连到右端点，流量1，费用为长度，表示x轴上这一段可以选择用这个线段。

这里我们发现有个坑：线段可能与x轴垂直。

我一开始以为是交点个数不能超过k，于是直接continue了，后来发现题读错了，是相交线段个数。

怎么办呢？我们要自己向自己连边了？

拆点！！x轴每个位置拆成入点和出点，然后有垂直的就入点向出点连边即可。

大概长这样：

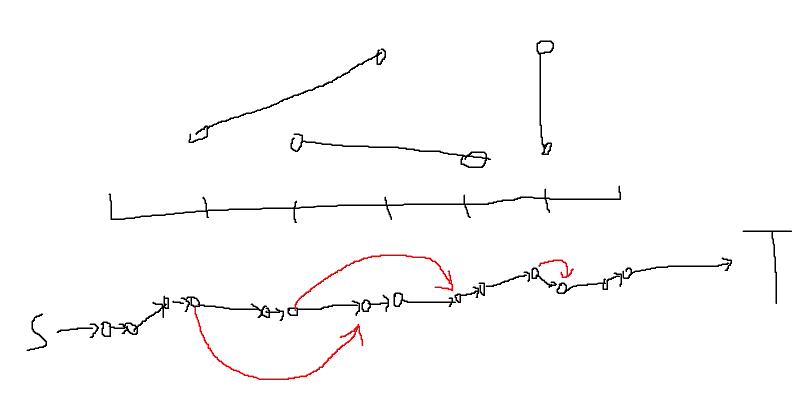
然后跑最大费用最大流即可。

听说坐标算距离那里会爆int...long long大法好(滑稽)

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <cmath>
  6 
  7 typedef long long LL;
  8 const int N = 5010, M = 50010;
  9 const LL INF = 0x3f3f3f3f3f3f3f3fll;
 10 
 11 struct Edge {
 12     int nex, v, c;
 13     LL len;
 14 }edge[M << 1]; int top = 1;
 15 
 16 int e[N], pre[N], Time, flow[N], l[N], r[N], X[N];
 17 LL d[N];
 18 std::queue<int> Q;
 19 bool vis[M];
 20 LL lenth[N];
 21 
 22 inline void add(int x, int y, int z, LL w) {
 23     top++;
 24     edge[top].nex = e[x];
 25     edge[top].v = y;
 26     edge[top].c = z;
 27     edge[top].len = w;
 28     e[x] = top;
 29     top++;
 30     edge[top].v = x;
 31     edge[top].c = 0;
 32     edge[top].len = -w;
 33     edge[top].nex = e[y];
 34     e[y] = top;
 35     return;
 36 }
 37 
 38 inline bool SPFA(int s, int t) {
 39     memset(d, 0x3f, sizeof(d));
 40     d[s] = 0;
 41     vis[s] = Time;
 42     flow[s] = INF;
 43     Q.push(s);
 44     while(!Q.empty()) {
 45         int x = Q.front();
 46         Q.pop();
 47         vis[x] = 0;
 48         for(int i = e[x]; i; i = edge[i].nex) {
 49             int y = edge[i].v;
 50             if(!edge[i].c) {
 51                 continue;
 52             }
 53             if(d[y] > d[x] + edge[i].len) {
 54                 d[y] = d[x] + edge[i].len;
 55                 pre[y] = i;
 56                 flow[y] = std::min(flow[x], edge[i].c);
 57                 if(vis[y] != Time) {
 58                     vis[y] = Time;
 59                     Q.push(y);
 60                 }
 61             }
 62         }
 63     }
 64     return d[t] < INF; // error 0
 65 }
 66 
 67 inline void update(int s, int t) {
 68     int f = flow[t], i = pre[t];
 69     //printf("update : ");
 70     while(t != s) {
 71         //printf("%d ", t);
 72         edge[i].c -= f;
 73         edge[i ^ 1].c += f;
 74         t = edge[i ^ 1].v;
 75         i = pre[t];
 76     }
 77     //puts("");
 78     return;
 79 }
 80 
 81 LL solve(int s, int t, LL &cost) {
 82     int ans = 0;
 83     cost = 0;
 84     Time = 1;
 85     while(SPFA(s, t)) {
 86         ans += flow[t];
 87         cost += flow[t] * d[t];
 88         update(s, t);
 89         Time++;
 90     }
 91     return ans;
 92 }
 93 
 94 int main() {
 95     int n, k, temp = 0;
 96     scanf("%d%d", &n, &k);
 97     for(int i = 1, x, y; i <= n; i++) {
 98         scanf("%d%d", &l[i], &x);
 99         scanf("%d%d", &r[i], &y);
100         /*if(l[i] == r[i]) {
101             continue;
102         }*/
103         X[++temp] = l[i];
104         X[++temp] = r[i];
105         lenth[i] = (LL)(sqrt(1ll * (r[i] - l[i]) * (r[i] - l[i]) + 1ll * (y - x) * (y - x)));
106     }
107 
108     std::sort(X + 1, X + temp + 1);
109     temp = std::unique(X + 1, X + temp + 1) - X - 1;
110 
111     for(int i = 1; i <= n; i++) {
112         l[i] = std::lower_bound(X + 1, X + temp + 1, l[i]) - X;
113         r[i] = std::lower_bound(X + 1, X + temp + 1, r[i]) - X;
114         if(l[i] == r[i]) {
115             add(l[i], l[i] + temp, 1, -lenth[i]);
116             continue;
117         }
118         add(l[i] + temp, r[i], 1, -lenth[i]);
119     }
120     for(int i = 1; i < temp; i++) {
121         add(i + temp, i + 1, k, 0ll);
122         add(i, i + temp, k, 0ll);
123     }
124     add(temp, temp + temp, k, 0ll);
125 
126     int s = temp * 2 + 1, ss = temp * 2 + 2, t = temp * 2 + 3;
127     add(ss, s, k, 0);
128     add(s, 1, k, 0);
129     add(temp + temp, t, k, 0);
130     LL cost;
131     solve(ss, t, cost);
132     printf("%lld", -cost);
133 
134     return 0;
135 }

AC代码

①⑧深海机器人问题。top

费用流。

只能取一次，解决方案是连一条1流量，有费用的边和一条INF流量，无费用的边。

源点向所有起点连边，所有终点向汇点连边。

然后跑最大费用最大流即可。

洛谷题面有个坑，横纵坐标没有反...

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int N = 410, M = 200010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c, len;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], pre[N], Time, flow[N], n, m;
 13 std::queue<int> Q;
 14 bool vis[M];
 15 
 16 inline void add(int x, int y, int z, int w) {
 17     top++;
 18     edge[top].nex = e[x];
 19     edge[top].v = y;
 20     edge[top].c = z;
 21     edge[top].len = w;
 22     e[x] = top;
 23     top++;
 24     edge[top].v = x;
 25     edge[top].c = 0;
 26     edge[top].len = -w;
 27     edge[top].nex = e[y];
 28     e[y] = top;
 29     return;
 30 }
 31 
 32 inline bool SPFA(int s, int t) {
 33     memset(d, 0x3f, sizeof(d));
 34     d[s] = 0;
 35     vis[s] = Time;
 36     flow[s] = INF;
 37     Q.push(s);
 38     while(!Q.empty()) {
 39         int x = Q.front();
 40         Q.pop();
 41         vis[x] = 0;
 42         for(int i = e[x]; i; i = edge[i].nex) {
 43             int y = edge[i].v;
 44             if(!edge[i].c) {
 45                 continue;
 46             }
 47             if(d[y] > d[x] + edge[i].len) {
 48                 d[y] = d[x] + edge[i].len;
 49                 pre[y] = i;
 50                 flow[y] = std::min(flow[x], edge[i].c);
 51                 if(vis[y] != Time) {
 52                     vis[y] = Time;
 53                     Q.push(y);
 54                 }
 55             }
 56         }
 57     }
 58     return d[t] < INF; // error 0
 59 }
 60 
 61 inline void update(int s, int t) {
 62     int f = flow[t], i = pre[t];
 63     while(t != s) {
 64         edge[i].c -= f;
 65         edge[i ^ 1].c += f;
 66         t = edge[i ^ 1].v;
 67         i = pre[t];
 68     }
 69     return;
 70 }
 71 
 72 int solve(int s, int t, int &cost) {
 73     int ans = 0;
 74     cost = 0;
 75     Time = 1;
 76     while(SPFA(s, t)) {
 77         ans += flow[t];
 78         cost += flow[t] * d[t];
 79         update(s, t);
 80         Time++;
 81     }
 82     return ans;
 83 }
 84 
 85 inline int id(int x, int y) {
 86     return x * (m + 1) + y + 1;
 87 }
 88 
 89 int main() {
 90 
 91     int a, b;
 92     scanf("%d%d%d%d", &a, &b, &n, &m);
 93     // q = m  p = n
 94     for(int i = 0; i <= n; i++) {
 95         for(int j = 0; j < m; j++) {
 96             int x;
 97             scanf("%d", &x);
 98             add(id(i, j), id(i, j + 1), 1, -x);
 99             add(id(i, j), id(i, j + 1), INF, 0);
100         }
101     }
102     for(int j = 0; j <= m; j++) {
103         for(int i = 0; i < n; i++) {
104             int x;
105             scanf("%d", &x);
106             add(id(i, j), id(i + 1, j), 1, -x);
107             add(id(i, j), id(i + 1, j), INF, 0);
108         }
109     }
110     int S = (n + 1) * (m + 1) + 5;
111     int T = S + 1;
112     for(int i = 1, x, y, z; i <= a; i++) {
113         scanf("%d%d%d", &z, &x, &y);
114         add(S, id(x, y), z, 0);
115     }
116     for(int i = 1, x, y, z; i <= b; i++) {
117         scanf("%d%d%d", &z, &x, &y);
118         add(id(x, y), T, z, 0);
119     }
120 
121     int cost;
122     solve(S, T, cost);
123     printf("%d", -cost);
124 
125     return 0;
126 }

AC代码

①⑨餐巾计划问题。top

我居然把一个点拆成了五个点！还A了...

首先想到，应该用流量来代表每天的餐巾，这样保证最大流就是保证每天有餐巾。

然后先来个最简单的模型吧。直接排成一排，从源点买，源点向每天连边，费用为购买的钱，不限流。每天向汇点连边，限流表示每天用的餐巾数。洗就是n²枚举后面的天数，与当前点连边，费用为洗的费用。

然后发现不行：你洗的话，一条餐巾就用了两次，这样总流量(买的总餐巾数)就比每天餐巾数之和少了。所以需要额外的流量来处理这个一巾多用的问题。

我有个很朴素的想法：再开一条流量，在连边的时候费用取负，把买的费用减去。

然后发现又挂了：你可能洗多次啊！每次洗都减，那还了得？

这启示我们第二次洗的时候不消除买的钱。

这就要把新买来的和之前洗过的分开处理。

然后我考虑了一会三个点，发现不行，就建了4个点，进来两个，出去两个。

还有个小问题，你洗的数量不可能超过你买的数量吧...因为我从源点那里买的时候流量为INF，所以就要在洗的时候限流。然后又多出来一个点...

到最后每个点拆成了5个点...虽然正确性没问题了但是...

你见过1w个点，n²条边的费用流吗...

大概长这样...

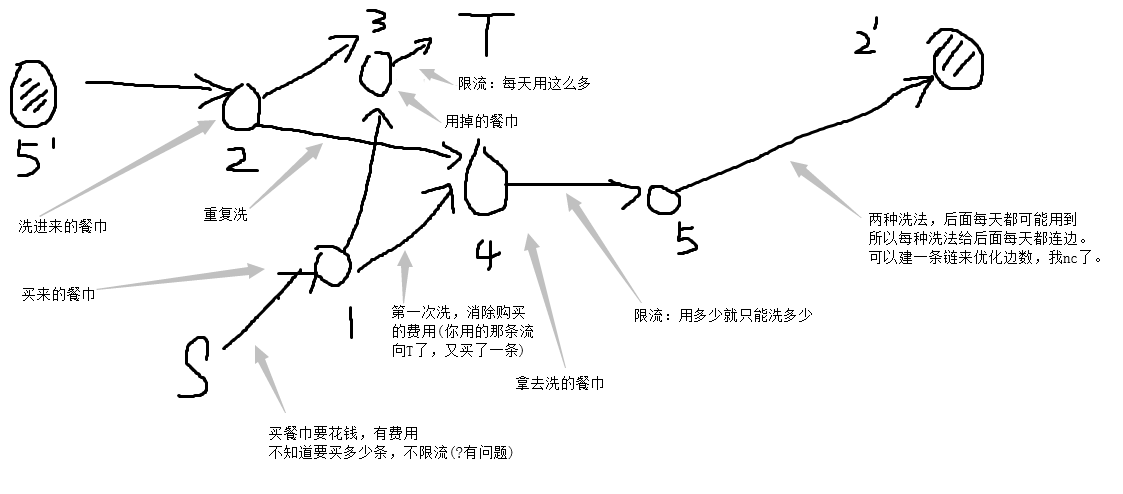
看起来比较恐怖......实测TLE，60分。

然后我优化连边一波，把n²连边改成每个5号点之间连流量INF，费用为0的链，就A了!!??

(虽然速度是正解的两倍...)

  1 #include <cstdio>
  2 #include <queue>
  3 #include <algorithm>
  4 #include <cstring>
  5 
  6 typedef long long LL;
  7 const int N = 20014, M = 2500010;
  8 const LL INF = 0x3f3f3f3f3f3f3f3fll;
  9 
 10 struct Edge {
 11     int nex, v;
 12     LL len, c;
 13 }edge[M << 1]; int top = 1;
 14 
 15 int e[N], pre[N], vis[N], Time;
 16 LL d[N], flow[N], use[N];
 17 std::queue<int> Q;
 18 
 19 inline void add(int x, int y, LL z, LL w) {
 20     top++;
 21     edge[top].v = y;
 22     edge[top].c = z;
 23     edge[top].len = w;
 24     edge[top].nex = e[x];
 25     e[x] = top;
 26 
 27     top++;
 28     edge[top].v = x;
 29     edge[top].c = 0;
 30     edge[top].len = -w;
 31     edge[top].nex = e[y];
 32     e[y] = top;
 33     return;
 34 }
 35 
 36 inline bool SPFA(int s, int t) {
 37     memset(d, 0x3f, sizeof(d));
 38     //printf("%lld \n%lld \n\n", d[t], INF);
 39     d[s] = 0;
 40     vis[s] = Time;
 41     flow[s] = INF;
 42     Q.push(s);
 43     while(!Q.empty()) {
 44         int x = Q.front();
 45         Q.pop();
 46         vis[x] = 0;
 47         //printf("d[%d] = %lld \n", x, d[x]);
 48         for(int i = e[x]; i; i = edge[i].nex) {
 49             int y = edge[i].v;
 50             if(edge[i].c && d[y] > d[x] + edge[i].len) {
 51                 d[y] = d[x] + edge[i].len;
 52                 flow[y] = std::min(flow[x], edge[i].c);
 53                 pre[y] = i;
 54                 if(vis[y] != Time) {
 55                     vis[y] = Time;
 56                     Q.push(y);
 57                 }
 58             }
 59         }
 60     }
 61     //printf("d < INF d = %lld %d \n", d[t], d[t] < INF);
 62     return d[t] < INF;
 63 }
 64 
 65 inline void update(int s, int t) {
 66     LL f = flow[t];
 67     //printf("update : f = %lld \n", f);
 68     while(s != t) {
 69         //printf("t = %d \n", t);
 70         int i = pre[t];
 71         edge[i].c -= f;
 72         edge[i ^ 1].c += f;
 73         t = edge[i ^ 1].v;
 74     }
 75     return;
 76 }
 77 
 78 inline LL solve(int s, int t, LL &cost) {
 79     LL ans = 0;
 80     cost = 0;
 81     memset(vis, 0, sizeof(vis));
 82     Time = 1;
 83     while(SPFA(s, t)) {
 84         ans += flow[t];
 85         cost += flow[t] * d[t];
 86         //printf("f = %lld  d = %lld \n", flow[t], d[t]);
 87         //printf("cost = %lld \n", cost);
 88         update(s, t);
 89         Time++;
 90     }
 91     return ans;
 92 }
 93 
 94 int n;
 95 inline int id(int i, int k) {
 96     return (k - 1) * n + i;
 97 }
 98 
 99 int main() {
100     int quick, slow;
101     LL sc, buy, qc;
102     scanf("%d", &n);
103     int s = n * 5 + 1, t = n * 5 + 2;
104     for(int i = 1; i <= n; i++) {
105         scanf("%lld", &use[i]);
106     }
107     scanf("%lld%d%lld%d%lld", &buy, &quick, &qc, &slow, &sc);
108 
109     for(int i = 1; i <= n; i++) {
110         add(s, i, INF, buy);
111         add(id(i, 3), t, use[i], 0);
112         add(i, id(i, 3), use[i], 0);
113         add(id(i, 2), id(i, 3), use[i], 0);
114         add(i, id(i, 4), use[i], -buy);
115         add(id(i, 2), id(i, 4), use[i], 0);
116         add(id(i, 4), id(i, 5), use[i], 0);
117         /*for(int j = i + quick; j <= n; j++) {
118             add(id(i, 5), id(j, 2), INF, qc);
119         }
120         for(int j = i + slow; j <= n; j++) {
121             add(id(i, 5), id(j, 2), INF, sc);
122         }*/
123         if(i + quick <= n) {
124             add(id(i, 5), id(i + quick, 2), INF, qc);
125         }
126         if(i + slow <= n) {
127             add(id(i, 5), id(i + slow, 2), INF, sc);
128         }
129         if(i < n) {
130             add(id(i, 5), id(i + 1, 5), INF, 0);
131         }
132     }
133 
134     LL cost;
135     solve(s, t, cost);
136     printf("%lld", cost);
137     return 0;
138 }

AC代码

接下来说正解：

这个题目都提醒我了，按照早晚拆点.....

然后，并非早->晚，而是S->晚->之后的早->T

S向晚连流量为当天餐巾数量的边，表示早上留下来的脏餐巾。

早向T连同样流量的边，表示今天用这么多。

S还要向早连收费的边，表示购买。

晚向后面的早连收费的边，表示洗。

晚向下一晚连INF，表示脏餐巾留着以后洗。

最后跑最小费用最大流即可。

  1 #include <cstdio>
  2 #include <queue>
  3 #include <algorithm>
  4 #include <cstring>
  5 
  6 typedef long long LL;
  7 const int N = 10014, M = 1000010;
  8 const LL INF = 0x3f3f3f3f3f3f3f3fll;
  9 
 10 struct Edge {
 11     int nex, v;
 12     LL len, c;
 13 }edge[M << 1]; int top = 1;
 14 
 15 int e[N], pre[N], vis[N], Time;
 16 LL d[N], flow[N], use[N];
 17 std::queue<int> Q;
 18 
 19 inline void add(int x, int y, LL z, LL w) {
 20     top++;
 21     edge[top].v = y;
 22     edge[top].c = z;
 23     edge[top].len = w;
 24     edge[top].nex = e[x];
 25     e[x] = top;
 26 
 27     top++;
 28     edge[top].v = x;
 29     edge[top].c = 0;
 30     edge[top].len = -w;
 31     edge[top].nex = e[y];
 32     e[y] = top;
 33     return;
 34 }
 35 
 36 inline bool SPFA(int s, int t) {
 37     memset(d, 0x3f, sizeof(d));
 38     //printf("%lld \n%lld \n\n", d[t], INF);
 39     d[s] = 0;
 40     vis[s] = Time;
 41     flow[s] = INF;
 42     Q.push(s);
 43     while(!Q.empty()) {
 44         int x = Q.front();
 45         Q.pop();
 46         vis[x] = 0;
 47         //printf("d[%d] = %lld \n", x, d[x]);
 48         for(int i = e[x]; i; i = edge[i].nex) {
 49             int y = edge[i].v;
 50             if(edge[i].c && d[y] > d[x] + edge[i].len) {
 51                 d[y] = d[x] + edge[i].len;
 52                 flow[y] = std::min(flow[x], edge[i].c);
 53                 pre[y] = i;
 54                 if(vis[y] != Time) {
 55                     vis[y] = Time;
 56                     Q.push(y);
 57                 }
 58             }
 59         }
 60     }
 61     //printf("d < INF d = %lld %d \n", d[t], d[t] < INF);
 62     return d[t] < INF;
 63 }
 64 
 65 inline void update(int s, int t) {
 66     LL f = flow[t];
 67     //printf("update : f = %lld \n", f);
 68     while(s != t) {
 69         //printf("t = %d \n", t);
 70         int i = pre[t];
 71         edge[i].c -= f;
 72         edge[i ^ 1].c += f;
 73         t = edge[i ^ 1].v;
 74     }
 75     return;
 76 }
 77 
 78 inline LL solve(int s, int t, LL &cost) {
 79     LL ans = 0;
 80     cost = 0;
 81     memset(vis, 0, sizeof(vis));
 82     Time = 1;
 83     while(SPFA(s, t)) {
 84         ans += flow[t];
 85         cost += flow[t] * d[t];
 86         //printf("f = %lld  d = %lld \n", flow[t], d[t]);
 87         //printf("cost = %lld \n", cost);
 88         update(s, t);
 89         Time++;
 90     }
 91     return ans;
 92 }
 93 
 94 int n;
 95 inline int id(int i, int k) {
 96     return (k - 1) * n + i;
 97 }
 98 
 99 int main() {
100     int quick, slow;
101     LL sc, buy, qc;
102     scanf("%d", &n);
103     int s = n * 2 + 1, t = n * 2 + 2;
104     for(int i = 1; i <= n; i++) {
105         scanf("%lld", &use[i]);
106     }
107     scanf("%lld%d%lld%d%lld", &buy, &quick, &qc, &slow, &sc);
108 
109     for(int i = 1; i <= n; i++) {
110         add(s, i, INF, buy);
111         add(s, n + i, use[i], 0);
112         add(i, t, use[i], 0);
113         if(i < n) {
114             add(n + i, n + i + 1, INF, 0);
115         }
116         if(i + quick <= n) {
117             add(n + i, i + quick, INF, qc);
118         }
119         if(i + slow <= n) {
120             add(n + i, i + slow, INF, sc);
121         }
122     }
123 
124     LL cost;
125     solve(s, t, cost);
126     printf("%lld", cost);
127     return 0;
128 }

AC代码

②〇数字梯形问题。top

嗯...比较裸吧。(当年在湖南跟logeadd想了半天没想出来...)

第一问，全部INF，跑费用流。

第二问，边流量为1，跑费用流。

第三问，点流量为1，跑费用流。

实现上每次重置了所有的流量。

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int N = 2010, M = 10010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c, len;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], pre[N], Time, flow[N], G[51][51], m, n, tot, ID[51][51];
 13 std::queue<int> Q;
 14 bool vis[M];
 15 
 16 inline void add(int x, int y, int z, int w) {
 17     top++;
 18     edge[top].nex = e[x];
 19     edge[top].v = y;
 20     edge[top].c = z;
 21     edge[top].len = w;
 22     e[x] = top;
 23     top++;
 24     edge[top].v = x;
 25     edge[top].c = 0;
 26     edge[top].len = -w;
 27     edge[top].nex = e[y];
 28     e[y] = top;
 29     return;
 30 }
 31 
 32 inline bool SPFA(int s, int t) {
 33     memset(d, 0x3f, sizeof(d));
 34     d[s] = 0;
 35     vis[s] = Time;
 36     flow[s] = INF;
 37     Q.push(s);
 38     while(!Q.empty()) {
 39         int x = Q.front();
 40         Q.pop();
 41         vis[x] = 0;
 42         for(int i = e[x]; i; i = edge[i].nex) {
 43             int y = edge[i].v;
 44             if(!edge[i].c) {
 45                 continue;
 46             }
 47             if(d[y] > d[x] + edge[i].len) {
 48                 d[y] = d[x] + edge[i].len;
 49                 pre[y] = i;
 50                 flow[y] = std::min(flow[x], edge[i].c);
 51                 if(vis[y] != Time) {
 52                     vis[y] = Time;
 53                     Q.push(y);
 54                 }
 55             }
 56         }
 57     }
 58     return d[t] < INF; // error 0
 59 }
 60 
 61 inline void update(int s, int t) {
 62     int f = flow[t], i = pre[t];
 63     while(t != s) {
 64         edge[i].c -= f;
 65         edge[i ^ 1].c += f;
 66         t = edge[i ^ 1].v;
 67         i = pre[t];
 68     }
 69     return;
 70 }
 71 
 72 int solve(int s, int t, int &cost) {
 73     int ans = 0;
 74     cost = 0;
 75     Time = 1;
 76     while(SPFA(s, t)) {
 77         ans += flow[t];
 78         cost += flow[t] * d[t];
 79         update(s, t);
 80         Time++;
 81     }
 82     return ans;
 83 }
 84 
 85 inline int id(int x, int y) {
 86     if(!ID[x][y]) {
 87         ID[x][y] = ++tot;
 88     }
 89     return ID[x][y];
 90 }
 91 
 92 inline void clear() {
 93     memset(vis, 0, sizeof(vis));
 94     return;
 95 }
 96 
 97 int main() {
 98     scanf("%d%d", &m, &n);
 99     int lm = (n + m) * n;
100     for(int i = 1; i <= n; i++) {
101         for(int j = 1; j <= m - 1 + i; j++) {
102             scanf("%d", &G[i][j]);
103         }
104     }
105     int s = N - 1, t = N - 2;
106     // part 1 NO
107     for(int i = 1; i < n; i++) {
108         for(int j = 1; j <= m - 1 + i; j++) {
109             add(id(i, j) + lm, id(i + 1, j), 1, 0);
110             add(id(i, j) + lm, id(i + 1, j + 1), 1, 0);
111         }
112     }
113     for(int i = 1; i <= n; i++) {
114         for(int j = 1; j <= m - 1 + i; j++) {
115             add(id(i, j), id(i, j) + lm, 1, -G[i][j]);
116         }
117     }
118     for(int i = 1; i <= m; i++) {
119         add(s, id(1, i), 1, 0);
120     }
121     for(int i = 1; i <= n + m - 1; i++) {
122         add(id(n, i) + lm, t, 1, 0);
123     }
124 
125     int cost;
126     solve(s, t, cost);
127     printf("%d\n", -cost);
128 
129     memset(vis, 0, sizeof(vis));
130     // part 2 CROSS+POINT
131     int temp = 1;
132     for(int i = 1; i < n; i++) {
133         for(int j = 1; j <= m - 1 + i; j++) {
134             edge[++temp].c = 1;
135             edge[++temp].c = 0;
136             edge[++temp].c = 1;
137             edge[++temp].c = 0;
138         }
139     }
140     for(int i = 1; i <= n; i++) {
141         for(int j = 1; j <= m - 1 + i; j++) {
142             edge[++temp].c = INF;
143             edge[++temp].c = 0;
144         }
145     }
146     for(int i = 1; i <= m; i++) {
147         edge[++temp].c = 1;
148         edge[++temp].c = 0;
149     }
150     for(int i = 1; i <= n + m - 1; i++) {
151         edge[++temp].c = INF;
152         edge[++temp].c = 0;
153     }
154 
155     solve(s, t, cost);
156     printf("%d\n", -cost);
157 
158     memset(vis, 0, sizeof(vis));
159     // part 3 CROSS
160     temp = 1;
161     for(int i = 1; i < n; i++) {
162         for(int j = 1; j <= m - 1 + i; j++) {
163             edge[++temp].c = INF;
164             edge[++temp].c = 0;
165             edge[++temp].c = INF;
166             edge[++temp].c = 0;
167         }
168     }
169     for(int i = 1; i <= n; i++) {
170         for(int j = 1; j <= m - 1 + i; j++) {
171             edge[++temp].c = INF;
172             edge[++temp].c = 0;
173         }
174     }
175     for(int i = 1; i <= m; i++) {
176         edge[++temp].c = 1;
177         edge[++temp].c = 0;
178     }
179     for(int i = 1; i <= n + m - 1; i++) {
180         edge[++temp].c = INF;
181         edge[++temp].c = 0;
182     }
183 
184     solve(s, t, cost);
185     printf("%d\n", -cost);
186 
187     return 0;
188 }

AC代码

②①家园。top

动态加点最大流。

唔......一开始看着有点像状压，发现不对，人有50个呢...

决定用一流量表示一个人。

然后飞船就用边表示，载客上限即为流量。

那么如何保证时间呢？自然想到了分层次，动态加边...(也可以二分)。

实现上就是枚举时间T，然后每次把飞船路径的两个点分层连起来。

然后跑最大流，如果超过k了就可以。

有个小坑，就是点必须分层，不能只用n个点。否则后面会搞不清时间先后顺序，导致你先走靠后时刻的边再走靠前时刻的边...

  1 #include <cstdio>
  2 #include <algorithm>
  3 #include <queue>
  4 #include <cstring>
  5 
  6 const int N = 10010, M = 1000010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c;
 10 }edge[M << 1]; int top = 1;
 11 
 12 struct Ship {
 13     int val, cnt;
 14     int a[20];
 15 }sh[30];
 16 
 17 int e[N], d[N], n;
 18 std::queue<int> Q;
 19 
 20 inline void add(int x, int y, int z) {
 21     //printf("add : %d %d \n", x, y);
 22 
 23     top++;
 24     edge[top].v = y;
 25     edge[top].c = z;
 26     edge[top].nex = e[x];
 27     e[x] = top;
 28 
 29     top++;
 30     edge[top].v = x;
 31     edge[top].c = 0;
 32     edge[top].nex = e[y];
 33     e[y] = top;
 34     return;
 35 }
 36 
 37 inline bool BFS(int s, int t) {
 38     memset(d, 0, sizeof(d));
 39     d[s] = 1;
 40     Q.push(s);
 41     while(!Q.empty()) {
 42         int x = Q.front();
 43         Q.pop();
 44         for(int i = e[x]; i; i = edge[i].nex) {
 45             int y = edge[i].v;
 46             if(!edge[i].c || d[y]) {
 47                 continue;
 48             }
 49             d[y] = d[x] + 1;
 50             Q.push(y);
 51         }
 52     }
 53     return d[t];
 54 }
 55 
 56 int DFS(int x, int t, int maxF) {
 57     if(x == t) {
 58         return maxF;
 59     }
 60     int ans = 0;
 61     for(int i = e[x]; i; i = edge[i].nex) {
 62         int y = edge[i].v;
 63         if(!edge[i].c || d[x] + 1 != d[y]) {
 64             continue;
 65         }
 66         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 67         if(!temp) {
 68             d[y] = 0;
 69         }
 70         ans += temp;
 71         edge[i].c -= temp;
 72         edge[i ^ 1].c += temp;
 73         if(ans == maxF) {
 74             break;
 75         }
 76     }
 77     return ans;
 78 }
 79 
 80 inline int solve(int s, int t) {
 81     int ans = 0;
 82     while(BFS(s, t)) {
 83         ans += DFS(s, t, INF);
 84     }
 85     return ans;
 86 }
 87 
 88 namespace ufs {
 89     int fa[N];
 90     inline int pre() {
 91         for(int i = 1; i < N; i++) {
 92             fa[i] = i;
 93         }
 94         return 0;
 95     }
 96     int odpa = pre();
 97     int find(int x) {
 98         if(x == fa[x]) {
 99             return x;
100         }
101         return fa[x] = find(fa[x]);
102     }
103     inline void merge(int x, int y) {
104         fa[find(x)] = find(y);
105         return;
106     }
107     inline bool check(int x, int y) {
108         return find(x) == find(y);
109     }
110 }
111 
112 inline int id(int x, int deep) {
113     if(x == N - 1 || x == N - 2) {
114         return x;
115     }
116     return deep * n + x;
117 }
118 
119 int main() {
120     int m, k, s = N - 1, t = N - 2;
121     scanf("%d%d%d", &n, &m, &k);
122     for(int i = 1; i <= m; i++) {
123         scanf("%d%d", &sh[i].val, &sh[i].cnt);
124         for(int j = 0; j < sh[i].cnt; j++) {
125             scanf("%d", &sh[i].a[j]);
126             if(sh[i].a[j] == 0) {
127                 sh[i].a[j] = s;
128             }
129             else if(sh[i].a[j] == -1) {
130                 sh[i].a[j] = t;
131             }
132             ufs::merge(sh[i].a[0], sh[i].a[j]);
133         }
134     }
135     if(!ufs::check(s, t)) {
136         printf("0");
137         return 0;
138     }
139     // -----------
140 
141     int ans = 0;
142     for(int T = 1; ; T++) {
143         //printf("T = %d ", T);
144         for(int i = 1; i <= n; i++) {
145             add(id(i, T - 1), id(i, T), INF);
146         }
147 
148         for(int i = 1; i <= m; i++) {
149             int turn = T % sh[i].cnt;
150             int last = turn - 1;
151             if(last < 0) {
152                 last = sh[i].cnt - 1;
153             }
154             add(id(sh[i].a[last], T - 1), id(sh[i].a[turn], T), sh[i].val);
155         }
156         ans += solve(s, t);
157         //printf("ans = %d \n", ans);
158         if(ans >= k) {
159             printf("%d", T);
160             break;
161         }
162     }
163 
164     return 0;
165 }

AC代码

②②火星探险问题。top

唯一的障碍就是输出方案.....

首先建图，如果是障碍就没有那个点。

然后从终点往前推，每次走BFS出一条流量，代表一个车的路径。

然后输出。(听起来好像很简单...)

一开始我比较脑残，预处理了一波不可能到的点，实际上它们根本不会有流量...(而且还搞出个bug来，害我出现负环)

  1 #include <cstdio>
  2 #include <queue>
  3 #include <algorithm>
  4 #include <cstring>
  5 
  6 typedef int LL;
  7 const int N = 20014, M = 2500010;
  8 const LL INF = 0x3f3f3f3f;
  9 
 10 struct POI {
 11     int x, y;
 12     POI(int X, int Y) {
 13         x = X;
 14         y = Y;
 15     }
 16 };
 17 
 18 struct Edge {
 19     int nex, v;
 20     LL len, c;
 21 }edge[M << 1]; int top = 1;
 22 
 23 int e[N], pre[N], vis[N], Time, n, m, fr[50][50], eg[50][50], G[50][50];
 24 LL d[N], flow[N], cnt[N];
 25 std::queue<int> Q;
 26 std::queue<POI> P;
 27 
 28 inline void add(int x, int y, LL z, LL w) {
 29     /*if(x == 200 || y == 200) {
 30         printf("add : %d %d \n", x, y);
 31     }*/
 32     top++;
 33     edge[top].v = y;
 34     edge[top].c = z;
 35     edge[top].len = w;
 36     edge[top].nex = e[x];
 37     e[x] = top;
 38 
 39     top++;
 40     edge[top].v = x;
 41     edge[top].c = 0;
 42     edge[top].len = -w;
 43     edge[top].nex = e[y];
 44     e[y] = top;
 45     return;
 46 }
 47 
 48 inline bool SPFA(int s, int t) {
 49     memset(d, 0x3f, sizeof(d));
 50     //printf("%lld \n%lld \n\n", d[t], INF);
 51     d[s] = 0;
 52     vis[s] = Time;
 53     flow[s] = INF;
 54     cnt[s] = 1;
 55     Q.push(s);
 56     while(!Q.empty()) {
 57         int x = Q.front();
 58         Q.pop();
 59         /*if(x == 202) {
 60             printf("x = 202 \n");
 61         }*/
 62         vis[x] = 0;
 63         //printf("d[%d] = %d \n", x, d[x]);
 64         for(int i = e[x]; i; i = edge[i].nex) {
 65             int y = edge[i].v;
 66             if(edge[i].c && d[y] > d[x] + edge[i].len) {
 67                 /*if(x == 202) {
 68                     printf("x = 202, y = %d \n", y);
 69                 }*/
 70                 //printf("x = %d, y = %d \n", x, y);
 71                 d[y] = d[x] + edge[i].len;
 72                 flow[y] = std::min(flow[x], edge[i].c);
 73                 pre[y] = i;
 74                 cnt[y] = cnt[x] + 1;
 75                 /*if(cnt[y] > N) {
 76                     printf("ERROR!!\n");
 77                 }*/
 78                 if(vis[y] != Time) {
 79                     vis[y] = Time;
 80                     Q.push(y);
 81                     /*if(y == 202) {
 82                         printf("y = 202 x = %d \n", x);
 83                     }*/
 84                 }
 85             }
 86         }
 87     }
 88     //printf("d < INF d = %lld %d \n", d[t], d[t] < INF);
 89     return d[t] < INF;
 90 }
 91 
 92 inline void update(int s, int t) {
 93     LL f = flow[t];
 94     //printf("update : f = %lld \n", f);
 95     while(s != t) {
 96         //printf("t = %d \n", t);
 97         int i = pre[t];
 98         edge[i].c -= f;
 99         edge[i ^ 1].c += f;
100         t = edge[i ^ 1].v;
101     }
102     return;
103 }
104 
105 inline LL solve(int s, int t, LL &cost) {
106     LL ans = 0;
107     cost = 0;
108     memset(vis, 0, sizeof(vis));
109     Time = 1;
110     while(SPFA(s, t)) {
111         ans += flow[t];
112         cost += flow[t] * d[t];
113         //printf("f = %lld  d = %lld \n", flow[t], d[t]);
114         //printf("cost = %lld \n", cost);
115         update(s, t);
116         Time++;
117     }
118     return ans;
119 }
120 
121 inline int id(int x, int y) {
122     return (x - 1) * m + y;
123 }
124 
125 inline void out(int x) {
126     int i = 1, j = 1;
127     while(1) {
128         if(G[i][j + 1] == 1 && G[i + 1][j] == 1) {
129             break;
130         }
131         if(G[i][j + 1] == -1) {
132             printf("%d %d\n", x, 1);
133             j++;
134         }
135         else {
136             printf("%d %d\n", x, 0);
137             i++;
138         }
139     }
140     return;
141 }
142 
143 inline void exout(int k) {
144     memset(fr, -1, sizeof(fr)); // 1 ->  0 |
145     memset(eg, 0, sizeof(eg));
146     P.push(POI(n, m));
147     int lm = n * m;
148     while(!P.empty()) {
149         int x = P.front().x;
150         int y = P.front().y;
151         P.pop();
152         //printf("P : %d %d \n", x, y);
153         x = id(x, y);
154         if(x == 1) {
155             break;
156         }
157         for(int i = e[x]; i; i = edge[i].nex) {
158             y = edge[i].v;
159             if(!edge[i].c || y == x + lm) {
160                 continue;
161             }
162             y -= lm;
163             int tx = (y - 1) / m + 1, ty = y % m;
164             if(!ty) {
165                 ty = m;
166             }
167             if(eg[tx][ty]) {
168                 continue;
169             }
170             //printf(" >>> y : %d %d \n", tx, ty);
171             if(y + 1 == x) { // ->
172                 fr[tx][ty] = 1;
173             }
174             else { // |
175                 fr[tx][ty] = 0;
176             }
177             eg[tx][ty] = i;
178             P.push(POI(tx, ty));
179         }
180     }
181     int x = 1, y = 1;
182     while(x != n || y != m) {
183         printf("%d %d\n", k, fr[x][y]);
184         edge[eg[x][y]].c--;
185         if(fr[x][y] == 1) {
186             y++;
187         }
188         else {
189             x++;
190         }
191     }
192     return;
193 }
194 
195 int main() {
196 
197     int k;
198     scanf("%d%d%d", &k, &m, &n);
199     for(int i = 1; i <= n; i++) {
200         for(int j = 1; j <= m; j++) {
201             scanf("%d", &G[i][j]);
202         }
203     }
204     for(int i = 1; i <= n; i++) {
205         G[i][m + 1] = 1;
206     }
207     for(int i = 1; i < m; i++) {
208         G[n + 1][i] = 1;
209     }
210 
211     for(int i = n; i >= 1; i--) {
212         for(int j = m; j >= 1; j--) {
213             bool f1 = G[i][j + 1] == 1 || G[i][j + 1] == -1;
214             bool f2 = G[i + 1][j] == 1 || G[i + 1][j] == -1;
215             if(f1 && f2) {
216                 G[i][j] = -1;
217             }
218         }
219     }
220 
221     /*puts("");
222     for(int i = 1; i <= n; i++) {
223         for(int j = 1; j <= m; j++) {
224             printf("%3d", G[i][j]);
225         }
226         puts("");
227     }*/
228 
229     if(G[1][1] == 1 || G[1][1] == -1) {
230         for(int i = 1; i <= k; i++) {
231             out(i);
232         }
233         return 0;
234     }
235     int lm = n * m;
236     int s = lm * 2 + 1, t = lm * 2 + 2;
237     for(int i = 1; i <= n; i++) {
238         for(int j = 1; j <= m; j++) {
239             if(G[i][j] == -1 || G[i][j] == 1) {
240                 continue;
241             }
242             int a = id(i, j);
243             if(G[i + 1][j] != -1 && G[i + 1][j] != 1 && i < n) {
244                 add(lm + a, id(i + 1, j), INF, 0);
245             }
246             if(G[i][j + 1] != -1 && G[i][j + 1] != 1) {
247                 add(lm + a, id(i, j + 1), INF, 0);
248             }
249             if(G[i][j] == 2) {
250                 add(a, lm + a, 1, -1);
251             }
252             add(a, lm + a, INF, 0);
253         }
254     }
255     add(s, 1, k, 0);
256     add(lm + lm, t, INF, 0);
257 
258     int ans = solve(s, t, lm);
259     //printf("%d  %d \n", ans, lm);
260     for(int i = 1; i <= k; i++) {
261         exout(i);
262     }
263 
264     return 0;
265 }

AC代码

②③航空路线问题。top

A->B->C的路径，可以转化为B->A和B->C两条。

然后用费用流搞一个经过城市最多的出来，输出方案。

注意：一条航线流量不能为1，因为可能被走两次，看这个SB样例：

2 1

a

b

a b

显然是有解的......

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 #include <map>
  6 #include <string>
  7 #include <iostream>
  8 
  9 typedef int LL;
 10 using std::string;
 11 const int N = 1010, M = 100010, INF = 0x3f3f3f3f;
 12 
 13 struct Edge {
 14     int nex, v, c, len;
 15 }edge[M << 1]; int top = 1;
 16 
 17 int e[N], d[N], vis[N], nex[N], pre[N], flow[N], Time;
 18 std::queue<int> Q;
 19 std::map<string, int> mp;
 20 string str[N];
 21 
 22 inline void add(int x, int y, LL z, LL w) {
 23     top++;
 24     edge[top].v = y;
 25     edge[top].c = z;
 26     edge[top].len = w;
 27     edge[top].nex = e[x];
 28     e[x] = top;
 29 
 30     top++;
 31     edge[top].v = x;
 32     edge[top].c = 0;
 33     edge[top].len = -w;
 34     edge[top].nex = e[y];
 35     e[y] = top;
 36     return;
 37 }
 38 
 39 inline bool SPFA(int s, int t) {
 40     memset(d, 0x3f, sizeof(d));
 41     //printf("%lld \n%lld \n\n", d[t], INF);
 42     d[s] = 0;
 43     vis[s] = Time;
 44     flow[s] = INF;
 45     Q.push(s);
 46     while(!Q.empty()) {
 47         int x = Q.front();
 48         Q.pop();
 49         vis[x] = 0;
 50         //printf("d[%d] = %lld \n", x, d[x]);
 51         for(int i = e[x]; i; i = edge[i].nex) {
 52             int y = edge[i].v;
 53             if(edge[i].c && d[y] > d[x] + edge[i].len) {
 54                 d[y] = d[x] + edge[i].len;
 55                 flow[y] = std::min(flow[x], edge[i].c);
 56                 pre[y] = i;
 57                 if(vis[y] != Time) {
 58                     vis[y] = Time;
 59                     Q.push(y);
 60                 }
 61             }
 62         }
 63     }
 64     //printf("d < INF d = %lld %d \n", d[t], d[t] < INF);
 65     return d[t] < INF;
 66 }
 67 
 68 inline void update(int s, int t) {
 69     LL f = flow[t];
 70     //printf("update : f = %lld \n", f);
 71     while(s != t) {
 72         //printf("t = %d \n", t);
 73         int i = pre[t];
 74         edge[i].c -= f;
 75         edge[i ^ 1].c += f;
 76         t = edge[i ^ 1].v;
 77     }
 78     return;
 79 }
 80 
 81 inline LL solve(int s, int t, LL &cost) {
 82     LL ans = 0;
 83     cost = 0;
 84     memset(vis, 0, sizeof(vis));
 85     Time = 1;
 86     while(SPFA(s, t)) {
 87         ans += flow[t];
 88         cost += flow[t] * d[t];
 89         //printf("f = %lld  d = %lld \n", flow[t], d[t]);
 90         //printf("cost = %lld \n", cost);
 91         update(s, t);
 92         Time++;
 93     }
 94     return ans;
 95 }
 96 
 97 int main() {
 98     int n, m;
 99     scanf("%d%d", &n, &m);
100     int s = n + n + 11, t = n + n + 12;
101     for(int i = 1; i <= n; i++) {
102         std::cin >> str[i];
103         mp[str[i]] = i;
104         add(i, i + n, (i == 1 || i == n) ? 2 : 1, -1);
105     }
106     for(int i = 1; i <= m; i++) {
107         std::cin >> str[0];
108         int x = mp[str[0]];
109         std::cin >> str[0];
110         int y = mp[str[0]];
111         if(x > y) {
112             std::swap(x, y);
113         }
114         add(y + n, x, 2, 0);
115     }
116     add(s, n, 2, 0);
117     add(n + 1, t, 2, 0);
118 
119     int cost;
120     int ans = solve(s, t, cost);
121 
122     if(ans != 2) {
123         printf("No Solution!");
124         return 0;
125     }
126 
127     printf("%d\n", -2 - cost);
128     int x = 1;
129     while(x != n) {
130         std::cout << str[x] << std::endl;
131         for(int i = e[x]; i; i = edge[i].nex) {
132             int y = edge[i].v;
133             if(y - n > x && edge[i].c) {
134                 x = y - n;
135                 edge[i].c--;
136                 edge[i ^ 1].c++;
137                 break;
138             }
139         }
140     }
141     while(x != 1) {
142         std::cout << str[x] << std::endl;
143         for(int i = e[x + n]; i; i = edge[i].nex) {
144             int y = edge[i].v;
145             if(edge[i ^ 1].c && y < x) {
146                 x = y;
147                 break;
148             }
149         }
150     }
151     std::cout << str[x];
152     return 0;
153 }