洛谷P4774 屠龙勇士

啊我死了。

肝了三天的毒瘤题......他们考场怎么A的啊。

---

大意：

给你若干个形如 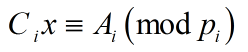的方程组，求最小整数解。

嗯......exCRT的变式。

考虑把前面的系数化掉：

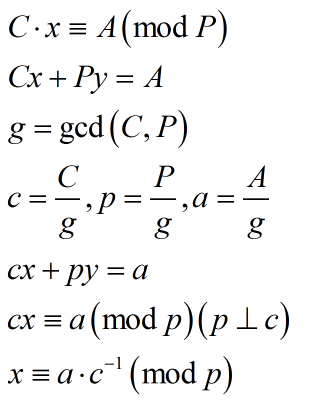
然后就是exCRT板子了。

我TM想要自己写出一个板子，然后GG了......

我快疯了。

然后抄了板子(滑稽)

注意细节，快速幂/乘的时候，b位置不要传负数。

#include <cstdio>
#include <set>
#include <algorithm>

typedef long long LL;
const int N = 100010;

std::multiset<LL> S;
std::multiset<LL>::iterator it;
int n, m, Time, vis[N];
LL a[N], p[N], awd[N], use[N];

LL Val;
LL gcd(LL a, LL b) {
    if(!b) {
        return a;
    }
    return gcd(b, a % b);
}
inline LL lcm(LL a, LL b) {
    return a / gcd(a, b) * b;
}
void exgcd(LL a, LL b, LL &x, LL &y) {
    if(!b) {
        x = Val / a;
        y = 0;
        return;
    }
    exgcd(b, a % b, x, y);
    std::swap(x, y);
    y -= (a / b) * x;
    return;
}
inline LL mod(LL a, LL c) {
    while(a >= c) {
        a -= c;
    }
    while(a < 0) {
        a += c;
    }
    return a;
}
inline LL mul(LL a, LL b, LL c) {
    LL ans = 0;
    a %= c;
    b %= c;
    while(b) {
        if(b & 1) {
            ans = mod(ans + a, c);
        }
        a = mod(a << 1, c);
        b = b >> 1;
    }
    return ans;
}
inline LL qpow(LL a, LL b, LL c) {
    LL ans = 1;
    a %= c;
    while(b) {
        if(b & 1) {
            ans = mul(ans, a, c);
        }
        a = mul(a, a, c);
        b = b >> 1;
    }
    return ans;
}
inline LL abs(LL a) {
    return a < 0 ? -a : a;
}
inline LL inv(LL a, LL c) {
    LL x, y;
    Val = 1;
    exgcd(a, c, x, y);
    return mod(x, c);
}
//----math----

inline void solve_p1() {
    LL ans = 0;
    for(int i = 1; i <= n; i++) {
        LL temp = (a[i] - 1) / use[i] + 1;
        ans = std::max(ans, temp);
    }
    printf("%lld\n", ans);
    return;
}

inline void solve_n1() {
    LL g = gcd(use[1], p[1]);
    if(a[1] % g) {
        puts("-1");
        return;
    }
    LL x, y;
    Val = a[1];
    exgcd(use[1], p[1], x, y);
    // use[1] * x + p[1] * y == a[1]
    LL gap = (use[1] / g);
    //printf("gap = %lld  y = %lld \n", gap, y);
    LL yy = (y % gap - gap) % gap;
    //printf("yy = %lld \n", yy);
    LL dt = (y - yy) / gap;
    //printf("dt = %lld \n", dt);
    x += dt * (p[1] / g);
    //printf("x = %lld \n", x);
    printf("%lld\n", x);
    return;
}

inline void solve_a() {
    LL large = 0;
    for(int i = 1; i <= n; i++) {
        large = std::max(large, (a[i] - 1) / use[i] + 1);
        LL g = gcd(use[i], p[i]);
        if(a[i] % g) {
            puts("-1");
            return;
        }
        if(p[i] == 1) {
            vis[i] = Time;
            continue;
        }
        //printf("%lld %lld %lld \n", use[i], p[i], a[i]);
        a[i] /= g;
        p[i] /= g;
        use[i] /= g;
        use[i] %= p[i];
        a[i] %= p[i];
        if(!use[i]) {
            if(!a[i]) {
                vis[i] = Time;
                continue;
            }
            else {
                puts("-1");
                //printf("%lld %lld %lld \n", use[i], p[i], a[i]);
                return;
            }
        }
        LL Inv, temp;
        Val = 1;
        exgcd(use[i], p[i], Inv, temp);
        Inv = mod(Inv, p[i]);
        //printf("Inv = %lld \n", Inv);
        a[i] = mul(Inv, a[i], p[i]);
    }
    // x = a[i] (mod p[i])

    /*for(int i = 1; i <= n; i++) {
        printf("x === %lld mod %lld \n", a[i], p[i]);
    }*/

    bool fd = 0;
    LL A = 0, P = 1;
    for(int i = 1; i <= n; i++) {
        //printf("%d \n", i);
        if(vis[i] == Time) {
            continue;
        }
        if(!fd) {
            A = a[i];
            P = p[i];
            fd = 1;
            continue;
        }
        // merge i
        LL x, y;
        LL C = ((a[i] - A) % p[i] + p[i]) % p[i];
        LL g = gcd(P, p[i]);
        if(C % g) {
            puts("-1");
            return;
        }
        Val = g;
        exgcd(P, p[i], x, y);
        x = mul(x, C / g, P / g * p[i]);
        A += mul(x, P, P / g * p[i]);
        P *= p[i] / g;
        A = (A + P) % P;
    }
    // x = A (mod P)
    // 1 * x + y * P = A

    LL x, y;
    Val = A;
    exgcd(1, P, x, y);
    x = mod(x, P);
    if(x < large) {
        x += P * ((large - x - 1) / P + 1);
    }
    printf("%lld\n", x);
    return;
}

inline void solve() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) {
        scanf("%lld", &a[i]);
    }
    for(int i = 1; i <= n; i++) {
        scanf("%lld", &p[i]);
    }
    for(int i = 1; i <= n; i++) {
        scanf("%lld", &awd[i]);
    }
    for(int i = 1; i <= m; i++) {
        LL x;
        scanf("%lld", &x);
        S.insert(x);
    }
    for(int i = 1; i <= n; i++) {
        it = S.upper_bound(a[i]);
        if(it != S.begin()) {
            it--;
        }
        use[i] = (*it);
        S.erase(it);
        S.insert(awd[i]);
    }

    //-------------------- p = 1  30pts -------
    bool f = 1;
    for(int i = 1; i <= n; i++) {
        if(p[i] > 1) {
            f = 0;
            break;
        }
    }
    if(f) {
        solve_p1();
        return;
    }

    //-------------------- n = 1  30pts -------
    if(n == 1) {
        solve_n1();
        return;
    }

    solve_a();
    return;
}

int main() {

    int T;
    scanf("%d", &T);
    for(Time = 1; Time <= T; Time++) {
        solve();
        if(Time < T) {
            S.clear();
        }
    }

    return 0;
}

一共提交了14次.......