论文--一种用于机械系统剩余使用寿命估计的新型双流自注意力神经网络--介绍

论文主要是针对不同传感器的监测数据未充分利用的问题，通过挖掘传感器内部信息差异作为辅助信息，来达到增强预测性能的目的。(原文中的使用自注意力机制这里不多介绍)

双流结构介绍

首先提出了一种数据转换方法来获得辅助数据，然后建立一个网络结构，将从原始数据和辅助数据中学习到的特征协同融合起来。

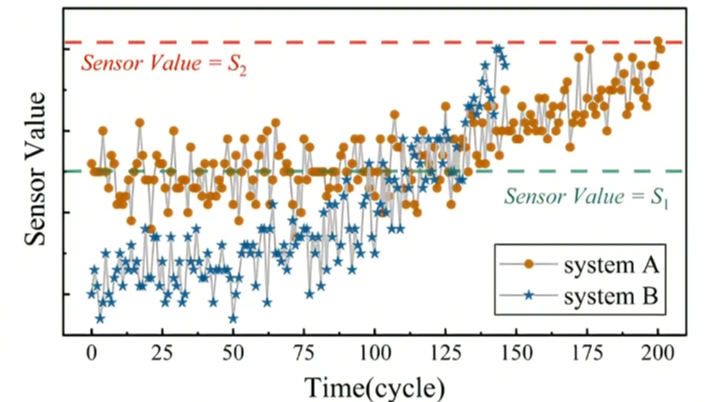
通常，机械系统的退化过程包括两个阶段：正常运行阶段和退化阶段[39]。在正常运行阶段，传感器的测量值是稳定的，而在退化阶段，传感器的测量值会发生明显变化。然而，由于机械系统的个体差异，在其正常状态下收集的传感器测量数据是不同的[25]。例如，图3显示了两个典型机械系统在整个生命周期内的传感器监测数据[38]。可以发现，： (1) 监测数据随着运行周期的增加而单调上升，当系统不能再使用时，传感器值接近相同的阈值S2。此外，机械系统的安全运行区域往往与传感器测量值直接相关[38]。这说明监测数据的绝对值包含有价值的退化信息，可以指示故障状态。(2) 系统正常状态下的监测数据是相互区别的，这就导致了即使是相同的传感器值，指示的健康状态也不相似。例如，当传感器数据在S1左右时，系统A处于正常运行阶段，而系统B则处于退化阶段。因此，我们可以抓住描述监测数据从初始状态到当前状态的相对变化的内部差异，以减少个体差异的负面影响，使神经网络更好地表达退化过程。

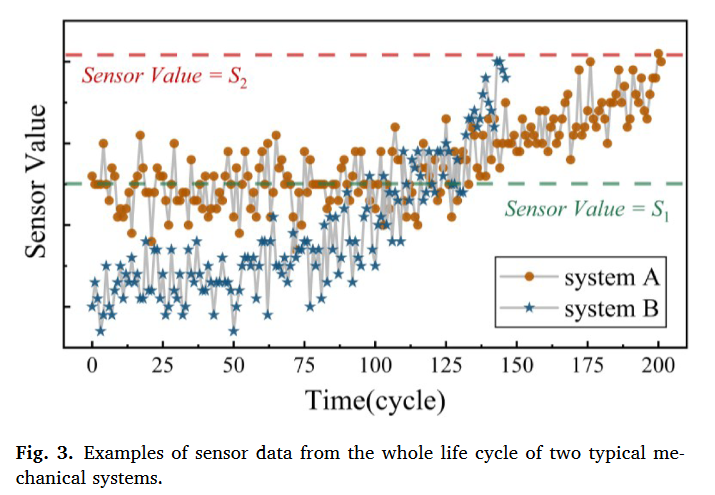
在这里，我们提出了一个用于特征提取和融合的双流框架，以探索更多的可用信息。这些信息包括： (1）由传感器实时测量的大量数据，称为原始数据；（2）监测数据的内部差异，称为辅助数据。为了获得原始数据，我们可以对原始监测数据应用常规的数据预处理方法，如传感器选择和数据归一化。此外，我们提出了一种数据转换算法，以获得代表监测数据从初始状态到当前状态的内部差异的辅助数据。这里，第i个样本的辅助数据可以表示为：

\[A_i=\left(A_i^1, A_i^2,\cdots,A_i^t,\cdots,A_i^T \right), for\quad i\in\left\{1,2,\cdots,n\right\}, \]

\[A_i^t=\left(a_{i,1}^t,a_{i,2}^t,\cdots,a_{i,m}^t,\cdots,a_{i,M}^t\right),for\quad t\in\left\{1,2,\cdots,T_i\right\}, \]

\[a_{i,m}^t=x_{i,m}^t-x_{i,m}^{initial}, for\quad m\in \left\{1,2,\cdots,M\right\} \]

其中，\(A_i^t∈R^M\)代表样本\(A_i\)中第\(t\)个时间步骤的辅助数据。\(x_{i,m}^t\)和\(x^{initial}_{i,m}\)分别表示第m个监测传感器的当前值（第\(t\)个时间步骤）和初始值。辅助数据\(a_{i,m}^t\)是通过减去\(x_{i,m}^t\)和\(x^{initial}_{i,m}\)得到的，表示健康状态的相对变化。对于单一运行条件下的机械系统，初始状态为\(x_{i,m}^t\)；而对于具有多种运行条件并在动态变化的运行条件下运行的机械系统，不同运行条件下的初始值是通过线性最小二乘法拟合得到。值得注意的是，辅助数据的获取是基于原始数据进行的。在数据处理后，对原始数据和辅助数据进行多头自适应操作，然后将提取的特征作为完整的降级特征进行级联。因此，受益于双流结构，特征提取子网络可以从监测数据中学习更多的信息，并促进RUL 的评估性能。

特征提取子网

多层感知器（MLP）是一种前馈神经网络，它通过将一组输入向量映射到输出向量来逼近数据中的线性和非线性关系。因此，在本研究中，MLP被用来执行RUL回归任务。MLP的网络结构由三部分组成：输入层（一层），隐藏层（一层或多层），以及输出层（一层）。同一层的神经元之间没有直接联系，而相邻层的神经元则通过加权求和实现完全连接。在这种方法中，由多头自我注意（MHSA）机制捕获的退化信息被用作MLP的输入。每个数据流的特征提取可以表示如下：

\[Original Stream:feature_{ori}=MHSA(X) \]

\[AuxiliaryStream:feature_{aux}=MHSA(A) \]

虽然RUL估计可以通过MLP结合每个单独的数据流提取的特征来实现，但本文提出采用双流结构，以丰富的特征来提高RUL估计的效果。因此，所有由MHSA机制提取的特征都是基于（11）的扁平化和串联。

\[Dual Stream:feature=concat(flatten(feature_{ori})+flatten(feature_{aux})) \]

然后MLP通过隐藏层进行近似计算，并在输出层获得估计的RUL。采用tanh函数作为激活函数。此外，我们在RUL预测子网络中使用了dropout技术[40]，以减少过拟合，增强DS-SANN的稳健性。

网络训练是通过反向传播（BP）算法完成的。由于RUL估计是一个回归问题，我们选择平均平方误差（MSE）作为网络参数优化的损失函数。这个函数描述了标记的RUL和估计的RUL之间的偏差，其表述如下：

\[loss=\frac{1}{N}\sum_{i=1}^N(RUL_i^{'}-RUL_i)^2, \]

其中\(N\)为样本数，\(RUL_{'}^i\)为估计值，\(RUL_i\)为标注值。通过修正和调整网络的权重和偏置向量，使损失函数最小化。此外，本文使用均方根算法（RMSProp）[41]作为优化算法来解决大规模数据的参数优化问题。

整体框架

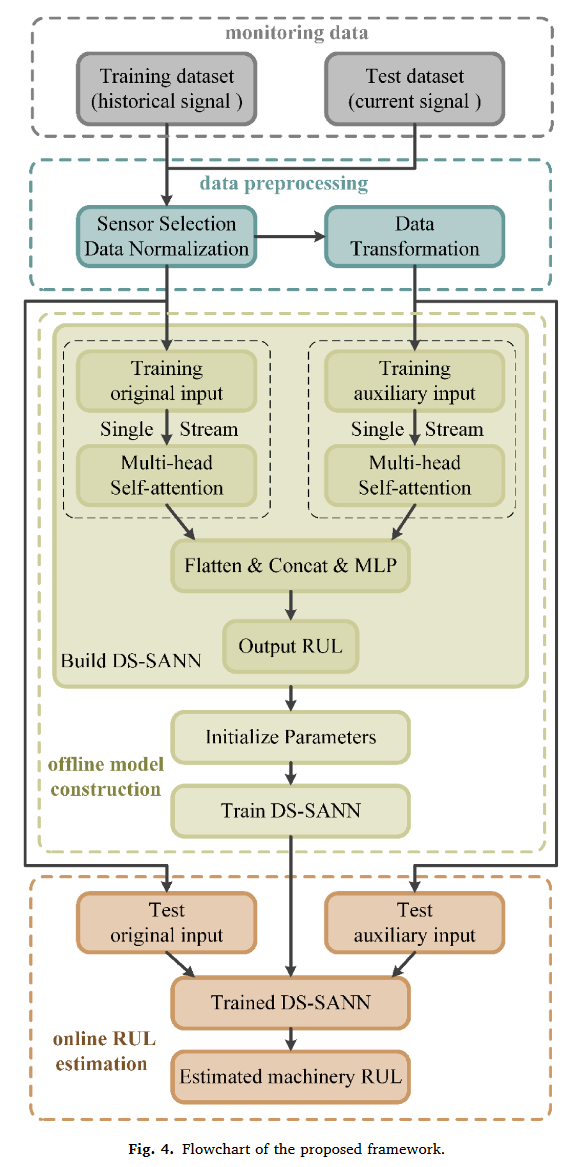
原文翻译已整理好，网址
https://www.cnblogs.com/huxiaohu52/p/17381925.html