干货来袭！3天0基础Python实战项目快速学会人工智能必学数学基础全套（含源码）（第2天）微积分篇：极限与导数、梯度下降与积分

@

目录

前言

前段时间，博主刚给大家分享了人工智能关于《线性代数》相关应用及知识点，紧接着第二篇关于微积分篇，其实说的就是大学期间，很多小伙伴们都头疼的高等数学里面的内容。

我记得我读大学的时候，大一上下学期我们分别学了高等数学上册和高等数学下册，这两本书的总学分还达到了我本科期间学习的所有课程的最高分——10分，总页数也达到了近1000页。

而每年的专升本，高等数学也成为必考的基础知识之一，考研涉及到的很多应用数学中运用到的基础知识也很多来自于高等数学。相信这里就可以看出高等数学对于大学教育的重要性了吧。

但对于《高等数学》这门学科来说，却成为不少小伙伴们的噩梦，课堂上的小伙伴们再怎么极尽脑汁听也听不懂，导致挂科补考率出奇地高。
在这里插入图片描述
而高等数学如此重要，却仅仅成为99%以上大学生学完后第一时间扔掉的书本之一，而现实情况下，大家把高等数学知识运用到工作中的也少之又少。

那很多人就好奇了，高等数学，在人工智能领域中到底有哪些用处呢？是不是人工智能领域中，用到高等数学，都是一些公式推导，理论深入等等呢？好吧，既然是分享数学，就还是拿出我严谨的思维和态度来。

我又翻出10多年前我的高数课本、笔记，老样子还是附上我个人成绩单吧，大家一起看看高等数学到底有什么知识需要我们在人工智能领域再学习研究。

在这里插入图片描述小伙伴们看到这里，是不是又要激动了，上次99分本不想说什么，你这还来个双90。88，我们还是不做朋友了吧！大家别激动，待会我就告诉大家这个考高分的小秘密，说不定下一个学霸就是你！

高数考高分的秘密就是培养出兴趣和热情，俗话说得好，兴趣是最好的导师，有了兴趣，你就成功了一半了。很多小伙伴们肯定会说：博主，你又在骗人了，高数能有什么兴趣和热情！
在这里插入图片描述让博主来帮你找找高数的兴趣和热情吧！！！

高数成绩好的小伙伴在大学期间被人另眼相看外，说不定就帮你找到你的另一半（有没有发现大学期间高数好的男同学们周围都围着一堆女同学问问题）。

大学3年后根据成绩来评选保研资格，高等数学这重要的10分学分将成为你的绝对优势。博主就靠高数的优势，第一年总成绩稳居年级第一，三年总成绩拿到年级第二，妥妥地保研成功。

在这里插入图片描述我再给大家打打鸡血，高等数学真要学起来，是有方法的！

很多小伙伴们学高等数学头疼的一个重要原因就是因为还是沿用初高中数学的思想和方法来学。

初高中数学，很多都靠一些固定的公式、定理、公理来获取解题思路和方法，而高等数学与它最大的区别就是，求解高等数学的根本在于对于一些复杂的无法套用固定公式来求解，甚至说是无解的问题，使用无限变化（取极限）的过程来实现的。

导数就是一种特殊模式的极限，是函数增量与自变量增量比的极限。

对于微积分来说，它的核心思想就是变换。就犹如古时候的智慧——“曹冲称象”，把大象“变换”成石头，石头的重量就是大象的总重量。

由“特殊问题”入手，得到“一般问题”。正如卡克所说“一般化和抽象是数学之最重要的功能。正是由于一般化和抽象，数学才能如此异乎寻常地有效。”在日常生活中也一样，要抓住事物的主要矛盾，遇事多总结、归纳，提高解决一般问题的能力。

最后，博主还是要和大家强调下，我们学人工智能，如果只是应用，不是深入理论或很深的算法研究，根本不需要从头到尾去学高等数学，更不用像大学一样去考试，如果真要考试，可能你考个20分就能达到人工智能的要求了！

因为人工智能涉及到高等数学的知识点仅仅只有其中的20%左右！

所以从现在开始你需要做的就是把以前的一切归零，跟着我继续三天轻松学习吧！

一、极限与导数

1.1 极限

我们首先从一个简单问题开始，来研究极限吧。

如果有一根长为1的木棍，每次从中间切段，切n次后，剩余部分长度为多少？如果n是一个非常大的数呢？这里面我相信聪明的小伙伴们能立马想到这就是传说中有名的两分法，不断的两分一个物品/路线，最后趋近于0。

\[\lim _{n \rightarrow \infty}\left(\frac{1}{2}\right)^{n} \rightarrow 0 \]

我们来看看极限的定义：
某一个函数中的某一个变量，此变量在变大(或者变小)的永远变化的过程中，逐渐向某一个确定的数值A不断地逼近的过程中，此变量的变化，被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”称作极限。

说白了，极限就是朝着一个目标出发，却总是达不到，只能无限趋近。而无限趋近到的这个目标值就可以定义为其极限。下面就是指：当变量x无限趋近于某一个数值x0时，对应的函数结果。

\[A=\lim _{x \rightarrow x_{0}} f(x) \]

给大家举两个求极限的例子：
在这里插入图片描述可以看到极限的求解也是要掌握一定的方法，如果左边把∞ 或者右边把0 直接带入，那就都不容易求出结果，但是如果做些如图中的变换，那就很容易就求出结果了。

1.2 导数

1.2.1 导数的由来与定义

我们先从一个连小学生都知道的方程（速度=路程÷时间）开始来了解导数吧。

比如说知道：路程s=t^2（即t的平方），那么t=2的时候，瞬时速度v是多少呢？

数学家的思维，就是将没学过的问题转化成学过的问题。

于是400年前的伟大科学家牛顿和莱布尼茨想了一个很聪明的办法，取一个“很短”的时间段Δt，先算算t=2到t=2+Δt这个时间段内，平均速度是多少。下面就是计算平均速度的过程。

\[\begin{array}{l} v=\frac{s}{t}&=\frac{(2+\Delta t)^{2}-2^{2}}{(2+\Delta t)-2} \\ &=\frac{4 \Delta t+\Delta t^{2}}{\Delta t} \\ &=4+\Delta t \end{array} \]

当Δt越来越小， 2+Δt就越来越接近2，时间段就越来越窄，越来越接近时刻，那么平均速度就越来越接近瞬时速度。如果Δt小到了0，平均速度4+Δt就变成了瞬时速度4。

是不是完美解决了瞬时速度的问题，而这就是导数的由来。

接下来我们就来看看导数的定义：

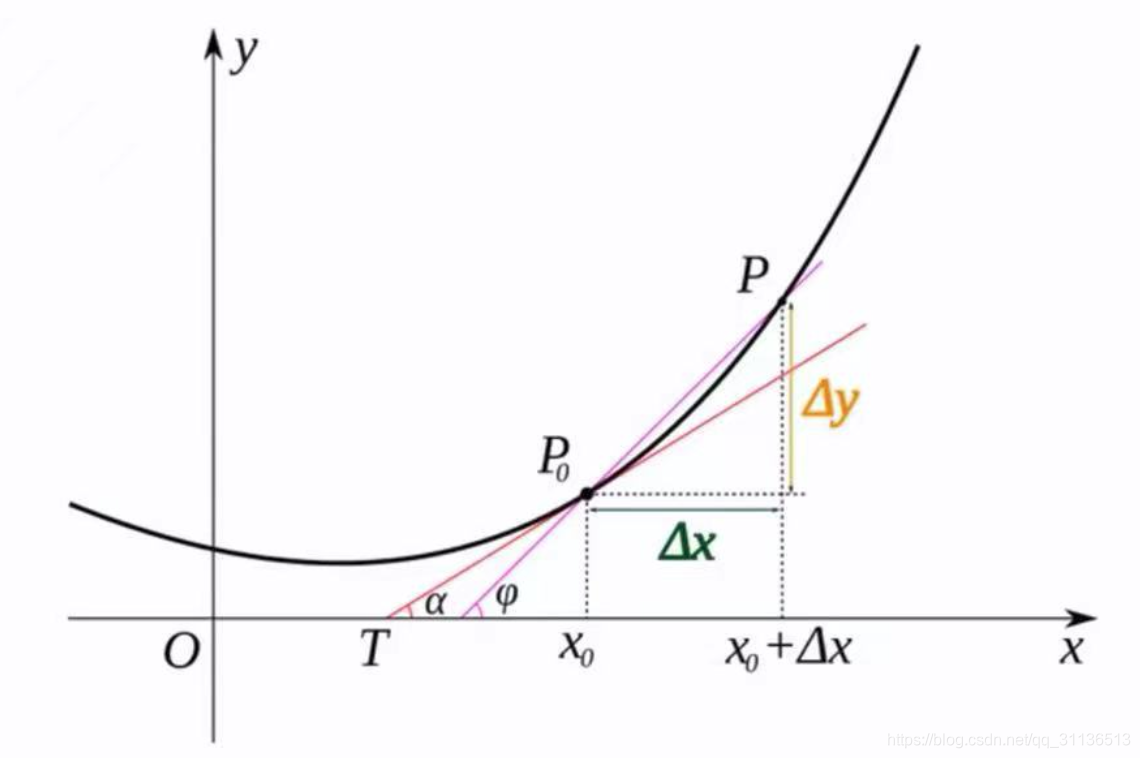
定义：当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'(x0) 或df(x0)/dx0。

在这里插入图片描述

\[\begin{aligned} f^{\prime}\left(x_{0}\right)=&\frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x} \\ = &\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x} \\ = &\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} \end{aligned} \]

1.2.2 常用的导数公式

对于常用的导数公式，大家只要在用到的时候，查下就好了，至于他们的推导过程，感兴趣的小伙伴们，可以用导数的定义去推导哈。

\[\begin{array}{cc} (C)^{\prime}=0 & (C x)^{\prime}=C \\ \left(x^{u}\right)^{\prime}=u x^{u-1} & \left(\frac{1}{x}\right)^{\prime}=-\frac{1}{x^{2}} \\ \left(e^{x}\right)^{\prime}=e^{x} & (\ln x)^{\prime}=\frac{1}{x} \\ (\sin x)^{\prime}=\cos x & (\cos x)^{\prime}=-\sin x \end{array} \]

1.2.3 导数的特点

导数有个重要的定理，那就是：

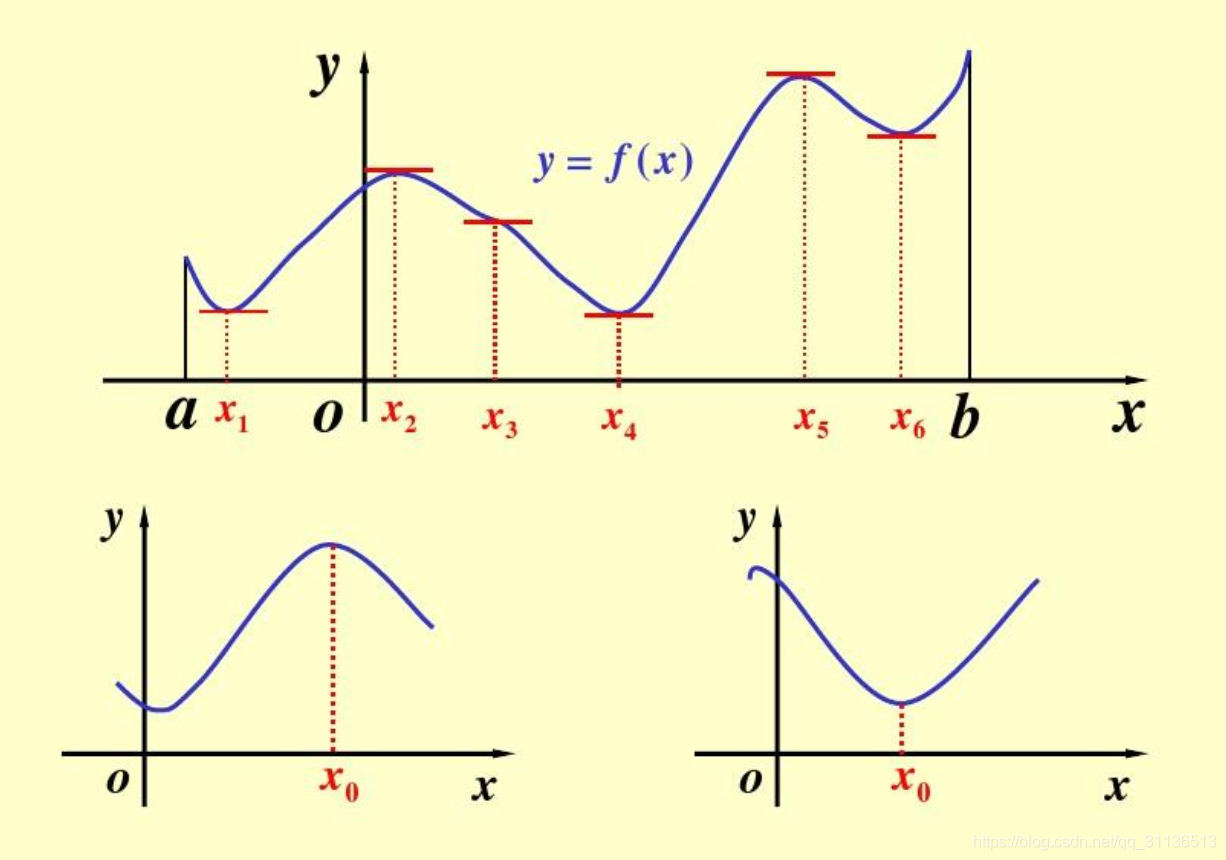
若函数f(x)在x0处可导，且x0是函数f(x)的极值点，那么函数f(x)在x=x0的导数f'(x0) =0。

注意：若去掉“函数f(x)在x0处可导”的条件，则函数的极值点x0处不一定有f'(x0) =0，如f(x)=｜x｜；此外，若f'(x0) =0，则x0不一定是极值点，如f(x)=x^3在x=0处，有f'(0) =0，但x=0不是f(x)=x^3的极值点。

大家可以对照下图，再好好理解下极大/小值、最小/最大值与导数为0的关系以及极值点的意思。

在这里插入图片描述最后，大家要注意，导数在机器学习、深度学习中的应用非常广泛，像最基础的梯度下降法求极值、反向传播通过链式求导（对复合函数，则用链式法则求导）来进一步调优确定参数、非线性函数泰勒展开、牛顿迭代法等等都有用到导数的概念。

二、模型求解与梯度下降法

2.1 导数与微分

小伙伴们在这里就会问了，怎么不是讲微分呢？

其实博主想了很久，对于微分来说，它在人工智能领域最重要的应用就是在对数据建立数学模型后，通过梯度下降来求解损失函数的极小值。所以讲梯度下降就是在给大家讲微分。

有很多人也会经常混淆导数和微分，但他们两又是息息相关的。从几何意义来说，在某点上的导数就是曲线上该点的切线的斜率，而该点上的微分就是那个切线的一元线性方程。微分的几何意义是用局部切线段近似代替曲线段，即非线性函数局部线性化。

所以，如果函数 \(y=f(x)\) 在 \(x_{0}\) 处的可导，那么在 \(x_{0}\) 处的导数为 \(f^{\prime}\left(x_{0}\right)\), 而函 数 \(y=f(x)\) 在 \(x_{0}\) 处的微分为 \(f^{\prime}\left(x_{0}\right) \Delta x\) 。两者之间相差一个因子，即自变量 \(x\) 的微分 \(\Delta x\) 。

小伙伴们，这下该清楚导数和微分的关系了吧。那我们就直接进入梯度下降法吧。

2.2 梯度下降法

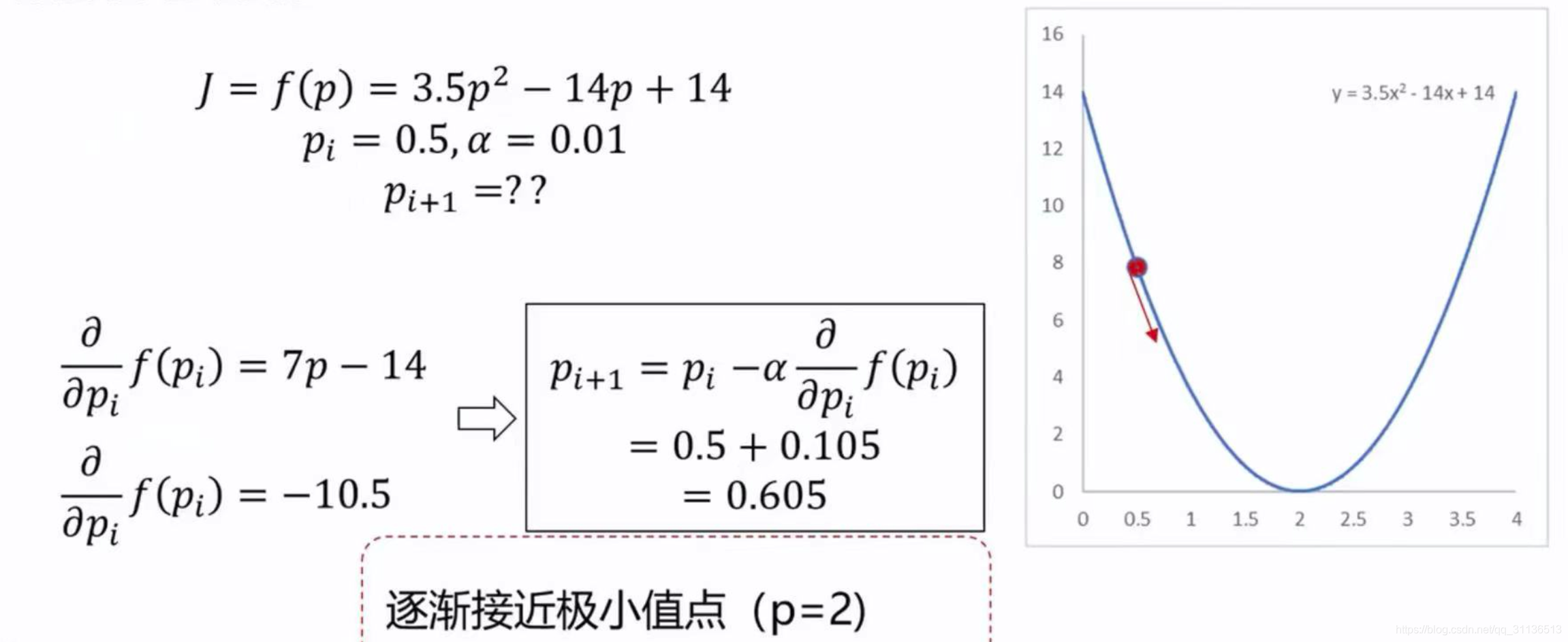
梯度下降法其实就是函数寻找极小值的一种方法。通过向函数上当前点对应梯度 (导数) 的反方向的规定步长距离点进行迭代搜索，直到在极小点收敛。

\[J=f(p) \underset{\text { 搜索方法 }}{\longrightarrow} p_{i+1}=p_{i}-\alpha \frac{\partial}{\partial p_{i}} f\left(p_{i}\right) \]

这里\(\frac{\partial}{\partial p_{i}} f\left(p_{i}\right)\)指的就是偏导数的概念，偏导数和导数的差别就在于，当函数有多个自变量，如f(x,z)函数分别对x、z求的导数就是偏导数，可表示为\(\frac{\partial}{\partial x_{0}} f\left(x_{0},z\right)\)，\(\frac{\partial}{\partial z_{0}} f\left(x,z_{0}\right)\)。

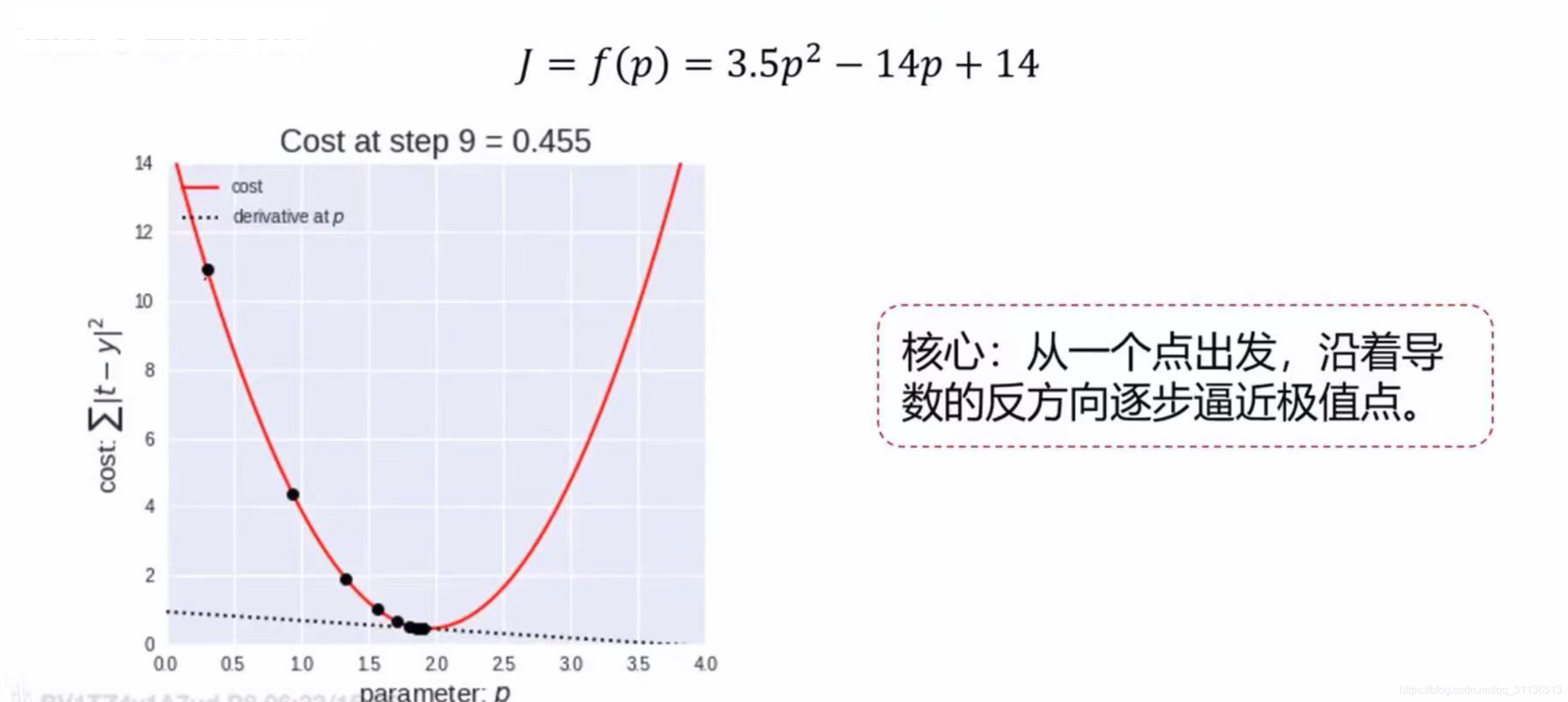
我们来举个最简单的例子，就是一个凸曲线的极小值来说明，梯度下降的迭代方法。从下面两图可以看出，运用梯度下降法，在第9步之后，就会逐步趋近于极小值点（p=2）了。
在这里插入图片描述在这里插入图片描述

2.3 应用案例：回归问题求解

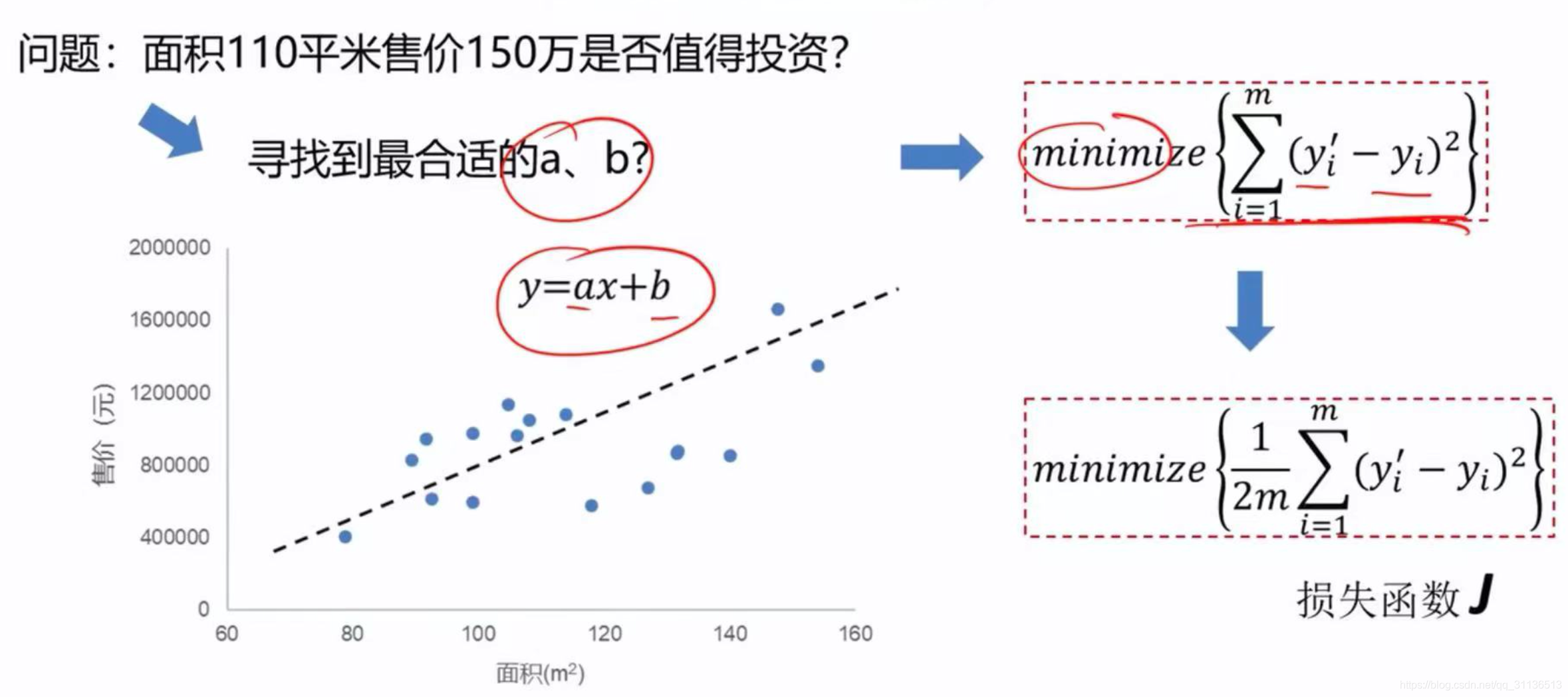
我们把一个现实中的买卖房产的问题，转化成一个线性数学模型Y=aX+b（看过我第一篇的小伙伴肯定很熟悉这个方程吧）。图中的小点就是我们拿到的样本数，分别不同房产面积对应不同的售价。
在这里插入图片描述在这里，我们目标就是寻找到最合适的a和b，来让我们建立的线性数学模型中同一个x求出的\(\mathrm{y}^{\prime}\)能够尽量接近真实的y。
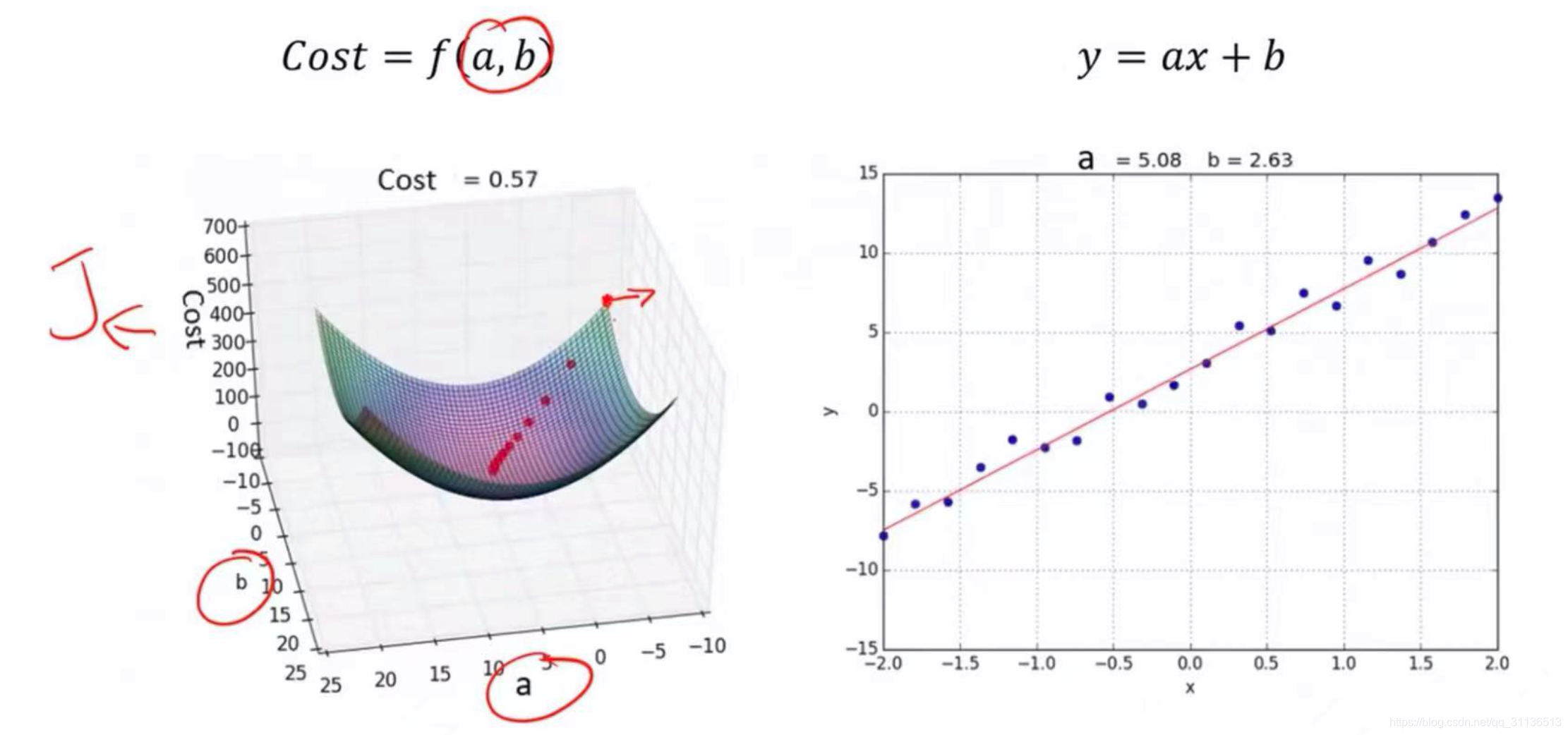
在这里插入图片描述这里我们进一步定义损失函数为：\(J= \frac{1}{2 m} \sum_{i=1}^{m}\left(y_{i}^{\prime}-y_{i}\right)^{2}\)，这里的J其实就是所有误差的总和除个平均。其实进一步想下，我们只要寻求到合适的a、b，让J最小就可以了。
在这里插入图片描述把它写成计算机能迭代的流程就如下：
在这里插入图片描述最后，我们通过不断地迭代计算，就能让损失函数不断地趋近于极小值，而我们也最终得到比较好的线形模型y=ax+b，这里a趋近于5.08，b趋近于2.63。

这时候，我们就可以代入x = 1.10/百平米，求得\(\mathrm{y}^{\prime}\)=8.218/十万，约82万。那聪明的你，就不会去投资150万来买这套房子了吧。

所以说学习微分/导数不要怕，So Easy！！！
在这里插入图片描述

三、积分

积分其实简单来说，就是导数/微分的逆运算。也就是说当你知道了函数的导函数，通过积分反求原函数。

积分被大量应用于求和，通俗的说是求曲边三角形的面积，这巧妙的求解方法是积分特殊的性质决定的。

积分可以分为不定积分和定积分。

3.1 不定积分

定义：函数\(f\) 的不定积分，是一个可导函数F且其导数等于原来的函数\(f\) ，即\(F^{\prime}=f\)

举个例子：
假设原函数\(f(x)=2x\)，那么我们可以得到一族可导函数\(F(x)\)，其导数均为\(2x\)，比如：

\[F(x)=x^{2}; F(x)=x^{2}+1 ; F(x)=x^{2}+10 \]

进一步，我们可以发现对于函数\(F(x)=x^{2}+C\)（其中\(C\)为任意常量），其导数均为\(f(x)=2x\)。所以函数的不定积分可以理解为其对应的反导数，有无穷多个。

3.2 定积分

定义：对于一个给空的正实值函数 \(f(x)\), 在一个实数区间上的定积分可以理解为在坐标平面上，由曲线、直线以及轴围成的曲边梯形的面积值。

我们可以用公式来表示定积分，其中F(b)、F(a)分别表示原函数\(f(x)\)对应的不定积分\(F(x)\)在\(x=b\)与\(x=a\)时候的函数值：

\[\int_{\mathbb{a}}^{b} f(x)dx=F(b)-F(a) \]

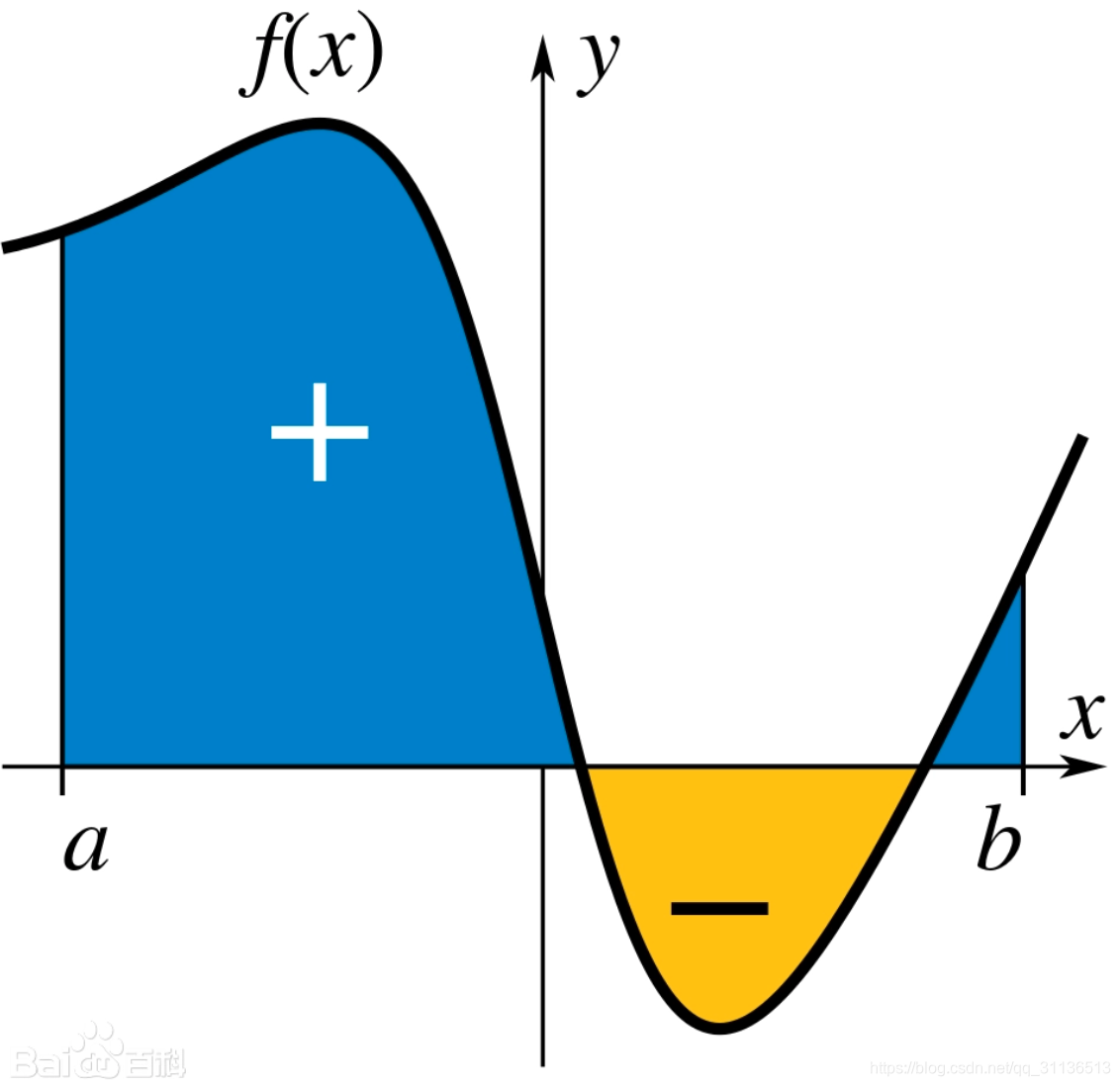
也可以用下图来说明定积分，就是x从a到b之间曲线和轴包围的面积之和，其中进行求和运算时，在x轴上方（蓝色）的面积为正，下方（黄色）的面积为负。

在这里插入图片描述

3.3 积分的重要应用：求解概率密度

定义：连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。

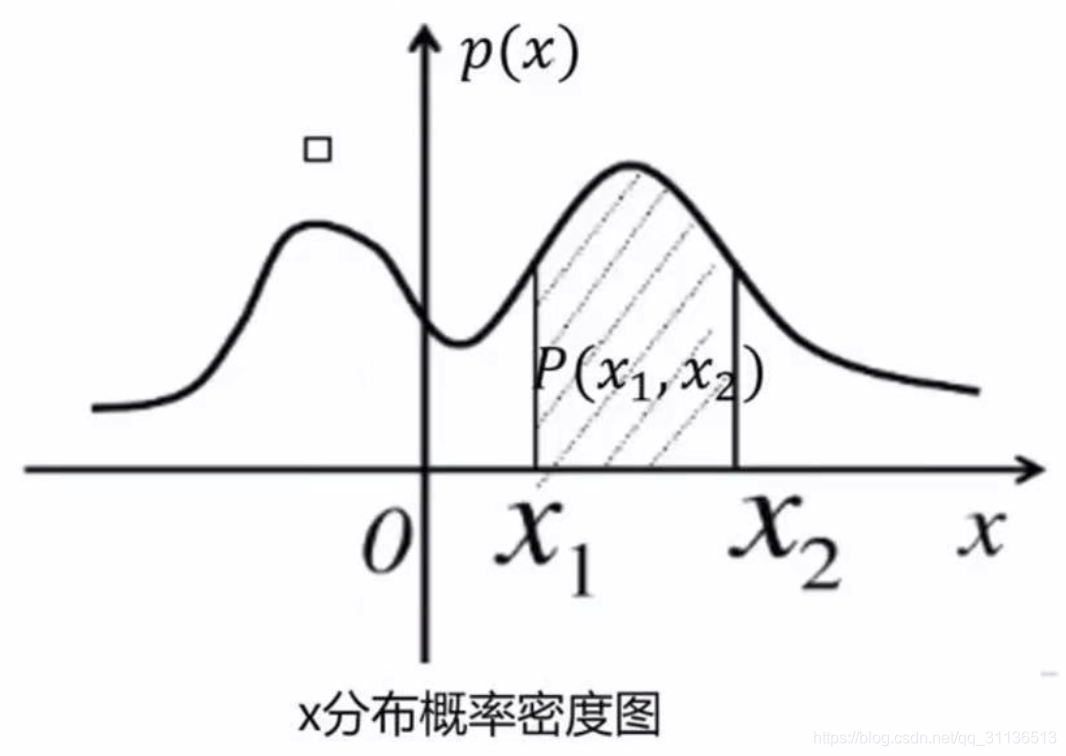
而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。当概率密度函数存在的时候，累积分布函数是概率密度函数的积分。

所以我们可以根据下图，来表示区间\(\left(x_{1}, x_{2}\right)\)的概率为\(x_{1}\)-\(x_{2}\)间的定积分：

\[\left.P\left(x_{1}, x_{2}\right)=\int_{x_{1}}^{x_{2}} p(x)dx\right. \]

在这里插入图片描述

3.3 常用的积分公式：

\[\begin{array}{ll} \int 0 \mathrm{~d} x=C & \int a \mathrm{~d} x=a x+C \\ \int x^{a} \mathrm{~d} x=\frac{1}{a+1} x^{a+1}+C & \int \frac{1}{x} \mathrm{~d} x=\ln |x|+C \\ \int e^{x} \mathrm{~d} x=e^{x}+C \\ \int \sin x \mathrm{~d} x=-\cos x+C & \int \cos x \mathrm{~d} x=\sin x+C \end{array} \]

四、实战：Python实现函数的微分与积分

1、安装python专用库sympy

sympy是一个Python的科学计算库，用一套强大的符号计算体系完成诸如多项式求值、求极限、解方程、求积分、微分方程、级数展开、矩阵运算等等计算问题。
详见：https://www.jianshu.com/p/339c91ae9f41

其官方介绍：
https://www.sympy.org/en/index.html

在这里插入图片描述其安装代码如下：

pip install sympy -i https://pypi.tuna.tsinghua.edu.cn/simple/

2、代码详解

我们通过下面两个任务来为大家讲解下如何在Jupyter Notebook中实现微积分的相关运算。

\[y_1=4x ; y_2=4x^{3}+3x^{2}+2; y_3=\frac{1}{x} \]

任务1: 求解\(y_1,y_2,y_3\)的在\(x=0\)处的极限

任务2： 计算以下函数的导数，分别记为 \(f_1,f_2,f_3\)

任务3: 计算\(f_1,f_2,f_3\)的不定积分函数，并与\(y_1,y_2,y_3\)对比

任务4：求解定积分：\(\int_{0}^{1} 2 x d x\)

使用Jupyter Notebook演示如下：

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

全部代码如下：

import sympy

# 首先定义x为一个符号，表示一个自变量
x = sympy.Symbol('x')
print(x)
print(type(x))

# 其次定义3个函数y1；y2；y3
y1 = 4 * x
y2 = 4 * x ** 3 + 3 * x ** 2 + 2
y3 = 1 / x
print(y1)
print(type(y1))
print(y2)
print(type(y2))
print(y3)
print(type(y3))

# 任务1:求解3个函数在x趋近于0时候到极限
# 求极限使用sympy.limit，传入3个参数：函数表达式，变量名，变量趋近值
L1 = sympy.limit(y1, x, 0)
L2 = sympy.limit(y2, x, 0)
L3 = sympy.limit(y3, x, 0)
print(L1)  # 结果为0
print(L2)  # 结果为2
print(L3)  # 结果为无穷大

# 任务2:求解3个函数的导数f1;f2;f3
# 求导使用sympy.diff函数，传入2个参数：函数表达式和变量名
f1 = sympy.diff(y1, x)
f2 = sympy.diff(y2, x)
f3 = sympy.diff(y3, x)
print(f1)  # 结果为4
print(f2)  # 结果为12*x**2 + 6*x
print(f3)  # 结果为-1/x**2

# 任务3:求解3个f1;f2;f3的不定积分函数F1；F2；F3
# 求不定积分使用sympy.integrate函数，传入2个参数：函数表达式和变量名
# 注意这里求解结果，省掉了常量C
F1 = sympy.integrate(f1, x)
F2 = sympy.integrate(f2, x)
F3 = sympy.integrate(f3, x)
print(F1)  # 结果为4*x 与 y1 一致
print(F2)  # 结果为4*x**3 + 3*x**2  与 y2 相差常量 2
print(F3)  # 结果为1/x 与 y3 一致

# 求解函数f4 = 2 * x 在0-1中的定积分 F4
# 使用sympy.integrate函数求定积分，传入函数表达式和积分变量、积分下限、上限
f4 = 2 * x
F4 = sympy.integrate(f4, (x, 0, 1))
print(F4)  # 结果为1，与我们口算结果一致（先求不定积分为F（x）= x^2+C，然后计算F（1）-F（0）=1）

总结

好啦，到这里就结束关于人工智能必学数学基础第二天微积分篇了，相信小伙伴们从极限与导数、微分与梯度下降、积分及其相关应用都有了一定的了解，并且也通过实战编程体会到了Python计算机编程语言对高等数学的强大计算能力了。

下一篇，我们会继续用浅显易懂、实战编程的方式为大家继续讲解关于人工智能必学数学基础——第三天概率分析篇，欢迎大家继续支持我 关注、收藏，点赞，一键三连。

另外如果有任何问题，可以随时评论区留言或者私信我。

本文只供大家学习相关知识使用，不以任何商业盈利为目的，转载或分享请注明相关来源。如涉及到相关侵权，请联系我删除。
欢迎志同道合者互相交流学习，可以加我微信号：Zhihua_Steven，或者扫以下二维码关注我的微信公众号。

在这里插入图片描述
posted @ 2023-03-14 14:02  虎啸AI  阅读(46)  评论(0)  编辑  收藏  举报