Threaded Compaction算法——Jonker算法
阅读《The Garbage Collection Handbook》第3章的Mark-Compaction垃圾回收算法时,对于Threaded Compaction总是无法理解。于是特意花了一些时间,总算是入门了,也搞懂了它的思想,写出来总结一下。如果文中有错误,还请指正。
Compaction算法概述
简单来说,Mark-Compaction算法做两件事情:mark和compaction。mark的工作是标记堆上的存活对象;compaction的工作是:1、把这些存活对象移动到该去的位置上;2、修改引用,令它们指向新的地址。既然要移动存活对象,那么移动的顺序有三种:1、任意顺序;2、滑动顺序;3、线性化顺序。通常来说,第一种顺序实现起来最简单,但会搞乱堆上对象之间的排列顺序,极大地伤害预取(prefetching)的效果,从而破坏了原有的局部性。在实践中几乎没有收集器使用这种方式;第二种顺序通常被认为是好的实现,因为它维持了堆上对象原有的顺序,仅仅是把对象之间的空洞(hole)挤压出来而已,因而没有拉低缓存的效果;3、第三种顺序可以认为是前一种的升级版。它是刻意地修改堆上对象的顺序,将未来可能一起使用的对象排列在一起,实现更好的空间局部性。一般来说,我们平时用到的收集器大多还是实现第二种顺序。
Compaction算法比较
首先,Mark-Compaction算法和Mark-Sweep、Copying和Reference Counting并称为四大基础垃圾回收算法。Java中我们熟知的并行收集器Parallel Collector(也称吞吐量收集器,throughput collector)中老年代的收集算法就是采用了Mark-Compaction的思想。当然了,它是多个线程并行地进行垃圾回收,因此名字是parallel collector。在阅读《The Garbage Collection Handbook》一书时,Two-Finger和Lisp2的Compaction算法理解起来相对容易些,唯独这个Threaded Compaction算法晦涩难懂。而该算法相比于前两种算法而言,有诸多优势,因此绝对值得我们好好研究下。下表总结了三种算法的优缺点:
| 算法 | 是否需要额外空间 | 遍历堆的次数 | 对象大小 | 顺序 |
| Two-Finger | 无需任何辅助空间 | 2 | 只能收集固定对象大小的堆 | 任意(随机) |
| Lisp2 | 要求对象槽能够容纳一个指针长度的数据 | 3 | 不要求对象大小固定 | 滑动(Sliding) |
| Threaded | 要求对象头部容纳指针 | 2 | 不要求对象大小固定 | 滑动 |
如果排除掉并行收集算法的话, 实际上Compaction算法还有一类比较终极的收集器:Compressor收集器。它比Threaded算法还要好。不过鉴于它不属于本文的研究范围,这里就不罗列它的特性了。
Jonker算法特性
就像上表展示的那样,Jonker算法无需额外的堆外存储空间来保存数据——事实上,的确有些算法或实现需要side table或bitmap(或bytemap)来保存数据。我们前面说过,Compaction算法都是要移动对象的,那么如果算法本身不需要额外的存储空间,那么就无法保存每个对象的新地址。那么,算法怎么知道要把对象移动到哪里呢?其实,算法只有在访问到对象的时候才能知道它要被移动到哪里。后面我们来看下它是怎么做到的。
Jonker算法也成为Threaded Compaction算法。这里的thread不是线程的意思,而是表示把多个对象通过指针串联在一起的过程。Threading的主要思想是:对于每个对象O,构造一个指针列表,里面的每个指针都指向O。这些指针就被称为串联指针(threaded pointer)。值得一提的是,这里的指针是指规范指针(canonical pointer),而不是内部指针(interior pointer)。前者是指指向对象首地址,也就是头部的指针(我们假设内存布局中头部永远位于对象的最前部);后者是指指向对象某个字段或槽(slot)的指针。由于不借助任何辅助空间,threaded pointer会被保存在对象的头部——这不算太“过分”,毕竟通常来说header word都足以容纳一个地址信息。除此之外,这个算法还要求header中保存的地址信息要能和其他数据区分开来——这个要求有点困难了。
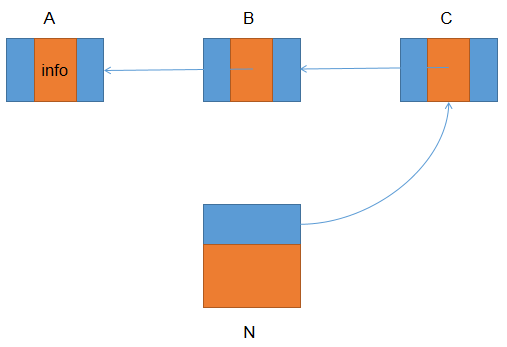
下面举一个例子展示下什么叫threading。下图(我直接使用了书中的例子)是一个4个对象的堆,其中A、B和C都引用了N:
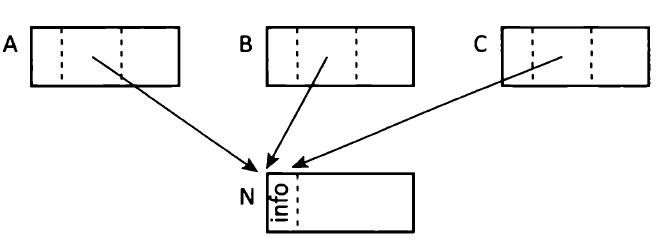
当threading结束的时候,所有指向N的指针都被逆转了方向,全部从对象N出发,依次串接在一起,如下图所示:
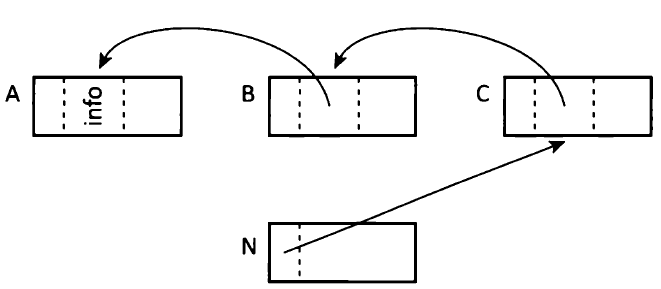
具体的threading代码很简单,大约只有以下几行:
thread(ref):
if *ref != null
*ref, **ref <- **ref, ref
它的主要功能是将ref指针逆转,让ref指向*ref指向的对象,而让*ref指向ref所在对象。如果拿上面的例子来说,当我们按照A、B、C和N的顺序遍历堆的话,那么第一个调用thread方法的ref就是A,*ref就是N的地址,**ref实际上是对象N的header数据。那么执行完thread之后,A中将保存N的header头部数据,而N指向A,如下图所示:
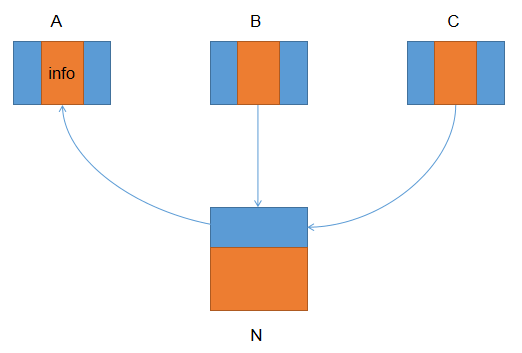
之后,算法遍历B时,整个堆上的引用关系将被调整为:
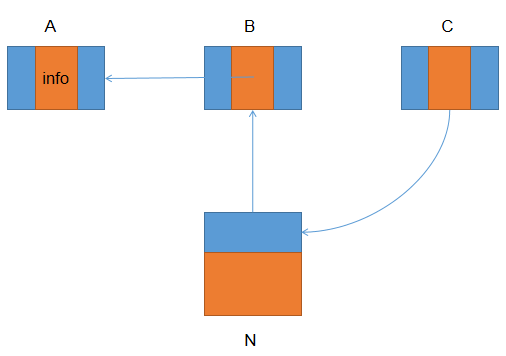
同理,遍历C时继续串接指针:
至此,A、B和C引用N的三个指针全部被串接在一起。现在算法可以通过N来访问到A、B和C,而且N的头部数据被搬到了A的字段中。串联好了指针之后,下面要更新指针指向的新地址N'。Jonker算法提供了一个update子函数用于将ref指针串联的所有指针全部unthread,并指向方法提供的第二个参数addr处。代码如下:
update(ref, addr):
tmp = *ref
while isReference(tmp)
*tmp, tmp = addr, *tmp
*ref = tmp
结尾处的*ref = tmp是为了将头部info数据恢复到ref所在的对象中。
下面使用一个图来说thread + update的操作流程:
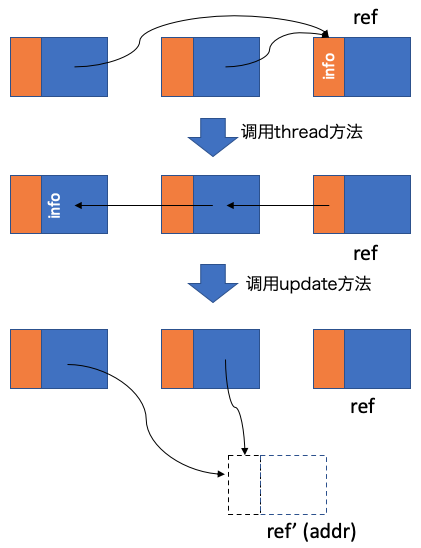
第一步我们之前解释过了,执行完thread之后所有指向ref的指针全部被逆向串联在一起并通过ref可以访问到。第二步是执行update(ref, addr)或update(ref, ref'),令之前指向ref的所有指针全部指到ref'或addr处。这样算法就实现了对ref对象compaction操作的重要一步:更新引用到前向地址,剩下的工作就是将ref对象移动到ref’所在的地址上。
第一遍遍历
事实上,Jonker算法第一遍遍历堆的工作就是这些,即从GC Roots开始,遍历堆上的所有对象,依次串联它们,如果某对象是存活对象,则调用update方法执行引用指向的调整。updateForwardReferences方法就是第一遍遍历堆的逻辑实现方法,代码如下:
updateForwardReferences():
for each field in Roots
thread(*field)
free = HeapStart
scan = HeapStart
while scan <= HeapEnd
if isMarked(scan)
update(scan, free)
for each field in Pointers(scan)
thread(field)
free += size(scan)
scan += size(scan)
这里的GC Roots通常是指从寄存器、栈上变量开始的引用,而HeapStart和HeapEnd分别对应于堆的起始地址和结束地址。由于我们要做compaction,我们通常会假设compaction会将存活对象全部挤压到从HeapStart开始的区域,这是free字段被赋值为HeapStart的原因。整个过程就像我刚才所说,基本上是thread + update的操作。我就不详细展开了。
第二遍遍历
第一遍遍历解决了调整compaction之后引用地址发生变化的问题,但没有执行compaction最关键的操作:移动对象。因此Jonker算法还需要做第二遍遍历进行对象的移动。下图展示了一个执行完第一遍遍历之后的堆分布:
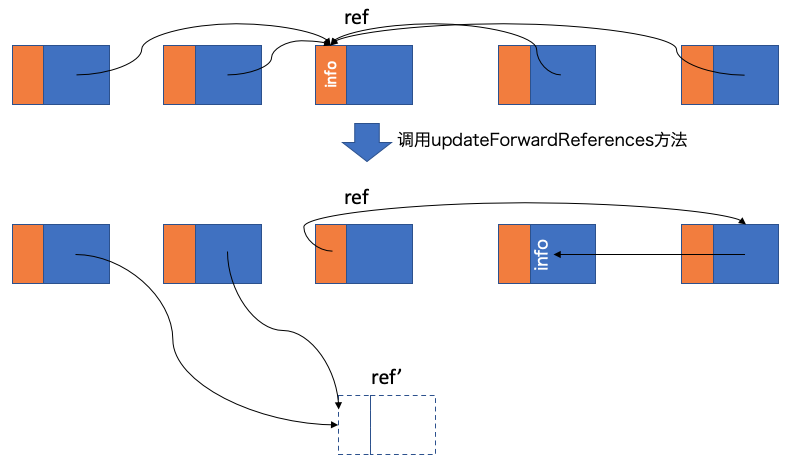
在ref之后的指针引用被称为后向指针(backwards pointer)。第一遍遍历结束之后,所有对象的后向指针全部也都串接在一起了,因此这一步的工作就是更新这些后向指针的引用地址,然后把对象移动到新的地址上去,如图所示:
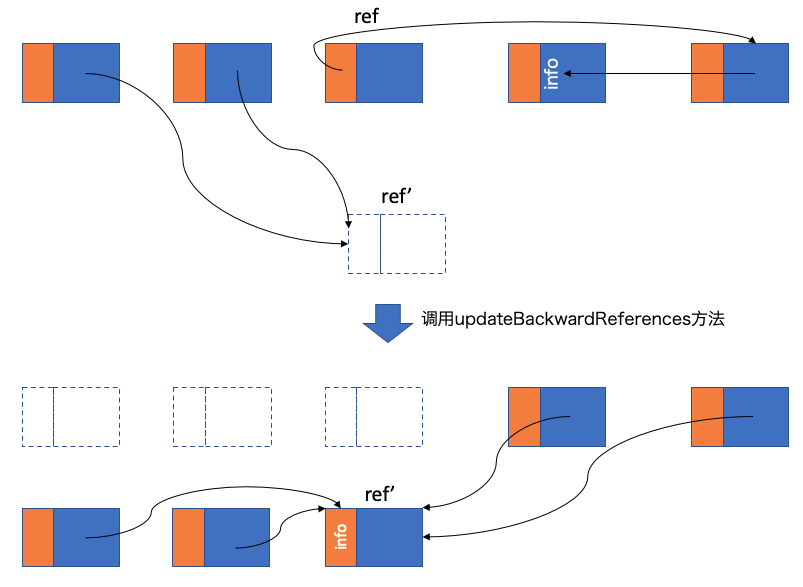
第二遍遍历的方法叫updateBackwardReferences。对于对象ref而言,它会将所有前向指针对象连同它自己全部compact到HeapStart开始的区域,之后调整后向指针对象引用新的地址ref'。代码如下:
updateBackwardReferences():
free = HeapStart
scan = HeapStart
while scan <= HeapEnd
if isMarked(scan)
update(scan, free)
move(scan, free)
free += size(scan)
scan += size(scan)
基本上,这个方法只做两件事情:更新地址引用以及移动对象。
总结
总体而言,Jonker算法要遍历堆两次,但无需额外的辅助空间,同时支持不同大小对象构成的堆。最重要的是,它能保持堆上原有的对象顺序,因而具有很好的局部性。要说它的缺陷,能想到的是算法需要访问对象很多次,另一个是该算法要求对象头部要能够明显区分出指针数据和其他数据。如果没有编译器和Runtime的支持,这个要求有时候是非常难实现的。不过,Jonker算法依然不失为一个非常优秀的Compaction算法。事实上,公认更加优秀的Compressor算法多多少少也有它的影子。

